Geometreg

Geometreg

Enghraifft o'r canlynol	maes o fewn mathemateg
Rhan o	mathemateg
Ffeiliau perthnasol ar Gomin Wicimedia

Tarddodd geometreg mewn sawl lle gwahanol drwy'r byd, yn annibynnol i'w gilydd, mewn ymgais ymarferol i ateb problemau'n ymwneud â hyd, arwynebedd a chyfaint gyda pheth disgyblaeth gwyddonol, ffurfiol i'w gael erbyn oes Thales yn y 6g CC. Erbyn y 3g roedd Euclid wedi'u ffurfioli ymhellach a cheir ei enw o fewn isddosbarth a adnabyddir heddiw fel geometreg Euclidaidd; dyma'r safon am ganrifoedd wedi hynny. Datblygodd Archimedes dechneg wych i gyfrifo arwynebedd a chyfaint yr hyn a enwir heddiw yn calcwlws cyfannol (neu integrol). Am y pymtheg cant o flynyddoedd dilynol, defnyddiwyd llawer o'i waith i ateb problemau'n ymwneud â mapio lleoliad y sêr a'r planedau. Ystyriwyd, felly, geometreg a seryddiaeth (yn y byd clasurol) yn rhan o'r un gangen (y Quadrivium) o'r saith celfyddyd bwysicaf i berson rhydd.

René Descartes a gyflwynodd y cysyniad o gyfesurynnau i'r astudiaeth ac ar yr un pryd datblygwyd algebra; mae'r ddau hyn yn ffurfio un o gerrig milltir pwysicaf y ddisgyblaeth gan y gellid, bellach, gynrychioli ffurfiau geometrig gyda ffwythiannau a hafaliadau. Yn ei dro (yn y 17g), chwaraeodd hyn ran eithriadol o bwysig yn yr hyn a elwir yn geometreg anfeidraidd. Dangosodd geometreg perspectif, hefyd, fod llawer mwy i geometreg, fel disgyblaeth, na jyglo rhifau. Ac yn sgil hyn, datblygwyd geometreg gwrthrychau gan Euler a Gauss gan arwain at isddosbarthiadau eraill o fewn geometreg a elwir yn dopograffi a geometreg gwahaniaethol.

Mae geometreg yn un disgyblaeth oddi fewn i Ofod:

Geometreg	Trigonometreg	Geometreg gwahaniaethol	Topoloeg	Geometreg ffractalaidd	Theori mesuredd

 

Gellir olrhain dechreuad cynharaf a gofnodwyd o geometreg i Mesopotamia hynafol a'r Aifft yn yr 2il fileniwm CC. Roedd geometreg gynnar yn gasgliad o egwyddorion a ddarganfuwyd yn empirig yn ymwneud â hyd, onglau, arwynebedd a chyfaint, a ddatblygwyd i ddiwallu rhywfaint o angen ymarferol wrth arolygu tir, adeiladu, seryddiaeth, ac amrywiol grefftau. Y testunau geometreg cynharaf y gwyddys amdanynt yw'r Papyrus Rhind o'r Aifft (2000-1800 CC) a Papyrus Moscow (tua 1890 CC), a'r tabledi clai Babilonaidd, megis Plimpton 322 (1900 CC). Er enghraifft, mae Papyrus Moscow yn rhoi fformiwla ar gyfer cyfrifo cyfaint pyramid cwtog, neu'r 'rhwystwm'. Mae tabledi clai diweddarach (350-50 CC) yn dangos bod seryddwyr Babilonaidd wedi gweithredu gweithdrefnau trapesiwm ar gyfer cyfrifo safle a symudiad Iau o fewn gofod cyflymder-amser. Roedd y gweithdrefnau geometrig hyn yn rhagweld Cyfrifianellau Rhydychen, gan gynnwys y theorem cyflymder cymedrig, y 14g. I'r de o'r Aifft sefydlodd y Nubiaid hynafol system geometreg gan gynnwys fersiynau cynnar o glociau haul.

Yn y 7g CC, defnyddiodd y mathemategydd Groegaidd Thales of Miletus geometreg i ddatrys problemau fel cyfrifo uchder pyramidiau a phellter llongau o'r lan. Dyma'r defnydd cyntaf o resymu diddwythol (deductive reasoning) a gymhwysir i geometreg, trwy ddeillio pedwar corollaries i theorem Thales. Sefydlodd Pythagoras yr Ysgol Pythagoraidd o feddwl, sy'n cael y clod am y prawf cyntaf o theorem Pythagoras, er bod datganiad y theorem wedi'i wyntyllu llawer iawn cyn ei oes ef. Datblygodd Eudoxus (408 - c. 355 CC) y dull parhaus (method of exhaustion), a oedd yn caniatáu cyfrifo arwynebedd a chyfeintiau ffigurau cromliniol, yn ogystal â theori cymarebau a oedd yn osgoi problem meintiau anghymarebol, a alluogodd geometregwyr dilynol i wneud datblygiadau sylweddol yn y maes hwn.

Tua 300 CC, chwyldroadwyd geometreg gan Euclid, ac ystyrir ei Elfennau, yn eang fel y llyfr testun mwyaf llwyddiannus a dylanwadol erioed; yn y gyfrol, cyflwynir trylwyredd mathemategol trwy ddefnyddio'r dull gwirebol a dyma'r enghraifft gynharaf o'r fformat hwn, sy'n dal i gael ei defnyddio mewn mathemateg heddiw. Hynny yw: diffiniad, gwireb, theorem, a phrawf. Er bod y rhan fwyaf o gynnwys yr Elfennau eisoes yn hysbys, trefnodd Euclid nhw yn un fframwaith rhesymegol cydlynol. Roedd yr Elfennau yn hysbys i bawb addysgedig yn y Gorllewin tan ganol yr 20g ac mae ei chynnwys yn dal i gael ei ddysgu mewn dosbarthiadau geometreg heddiw. Defnyddiodd Archimedes (c.  287–212 CC) o Syracuse y dull parhaus i gyfrifo'r arwynebedd o dan fwa parabola â chrynhoad y gyfres anfeidrol, a brasamcanodd pi yn hynod o gywir. Astudiodd hefyd y Sbiral Archimedes sy'n dwyn ei enw, a llwyddodd i gael fformiwlâu ar gyfer cyfeintiau arwynebau tro.

Cyfrannodd y mathemategwyr Indiaidd yn helaeth mewn geometreg hefyd. Mae'r Satapatha Brahmana (3g CC) yn cynnwys rheolau ar gyfer cystrawennau geometrig defodol sy'n debyg i'r Sulba Sutras. Yn ôl (Hayashi 2005) mae'r Śulba Sūtras yn cynnwys "yr ymadrodd llafar cynharaf sy'n bodoli o'r Theorem Pythagorean yn y byd, er ei fod eisoes yn hysbys i'r Hen Fabiloniaid. Maent yn cynnwys rhestrau o driawdau Pythagoraidd, sy'n achosion penodol o hafaliadau Diophantine. Yn llawysgrif Bakhshali, mae llond llaw o broblemau geometrig (gan gynnwys problemau ynghylch cyfeintiau solidau afreolaidd). Mae llawysgrif Bakhshali hefyd yn "gweithredu system gwerth lle degol gyda dot ar gyfer sero." Mae Aryabhatiya Aryabhata (499) yn cynnwys cyfrifiant o arwynebedd a chyfeintiau.

 

Ysgrifennodd Brahmagupta ei waith seryddol Brāhma Sphuṭa Siddhānta yn 628. Rhannwyd Pennod 12, yn cynnwys 66 o benillion Sansgrit, yn ddwy adran: "gweithrediadau sylfaenol", gan gynnwys y trydydd isradd, ffracsiynau, cymhareb a chyfran, a chyfnewid (barter) a "mathemateg ymarferol" (gan gynnwys cymysgedd, cyfresi mathemategol, ffigurau plân, pentyrru briciau, llifio pren, a phentyrru grawn). Yn yr adran olaf, nododd ei theorem enwog ar groeslinau pedrochrog cylchol. Roedd Pennod 12 hefyd yn cynnwys fformiwla ar gyfer arwynebedd pedrochrog cylchol, ynghyd â disgrifiad cyflawn o drionglau cymarebol (hy trionglau ag ochrau cymarebol ac arwynebedd cymarebol).

Yn Islam ganoloesol yr Oesoedd Canol, cyfrannodd mathemategwyr at ddatblygiad geometreg, yn enwedig geometreg algebraidd. Esgorodd Al-Mahani (ganwyd 853) ar y syniad o leihau problemau geometregol o fewn algebra. Gweithiodd Thābit ibn Qurra (a elwir yn Thebit yn Lladin; 836-901) â gweithrediadau rhifyddeg a gymhwyswyd i gymarebau meintiau geometregol, a chyfrannodd at ddatblygiad geometreg ddadansoddol. Daeth Omar Khayyám (1048–1131) o hyd i atebion geometrig i hafaliadau ciwbig. Roedd theoremau Ibn al-Haytham (Alhazen), Omar Khayyam a Nasir al-Din al-Tusi ar bedrochrau, gan gynnwys pedrochrog Lambert a phedrochrog Saccheri, yn ganlyniadau cynnar mewn geometreg hyperbolig, ac ynghyd â'u cynosodiadau amgen, fel gwireb Playfair, cafodd y gweithiau hyn gryn ddylanwad ar ddatblygiad geometreg nad yw'n Ewclidaidd ymhlith geometrau Ewropeaidd diweddarach, gan gynnwys Witelo (c. 1230 - c. 1314), Gersonides (1288–1344), Alfonso, John Wallis, a Giovanni Girolamo Saccheri.

Yn gynnar yn yr 17g, cafwyd dau ddatblygiad pwysig mewn geometreg. Y cyntaf oedd creu geometreg ddadansoddol, neu geometreg gyda chyfesurynnau a hafaliadau, gan René Descartes (1596–1650) a Pierre de Fermat (1601–1665). Roedd hyn yn rhagflaenydd angenrheidiol i ddatblygiad calcwlws a gwyddoniaeth feintiol ffiseg. Yr ail ddatblygiad pwysig oedd yr astudiaeth systematig o Geometreg dafluniol gan Girard Desargues (1591–1661). Dyma astudiaeth o briodweddau siapiau sy'n ddigyfnewid gan dafluniadau a thoriadau, yn enwedig gan eu bod yn ymwneud â phersbectif artistig.

Cafwyd dau ddatblygiad mewn geometreg yn y 19g hefyd: y cyntaf oedd darganfod geometregau an-Ewclidaidd, gan Nikolai Ivanovich Lobachevsky, János Bolyai a Carl Friedrich Gauss ac o lunio cymesuredd fel yr ystyriaeth ganolog yn Rhaglen Erlangen Felix Klein (a oedd yn cyffredinoli'r geometregau Ewclidaidd ac an-Ewclidaidd). Dau o brif geometregwyr oes oedd Bernhard Riemann (1826-1866), gan weithio'n bennaf gydag offer o ddadansoddiad mathemategol, a chyflwyno wyneb Riemann, a Henri Poincaré, sylfaenydd topoleg algebraidd a theori geometrig systemau deinamig. O ganlyniad i'r newidiadau mawr hyn yng nghysyniad geometreg, daeth y cysyniad o "ofod" yn rhywbeth cyfoethog ac amrywiol, a'r cefndir naturiol ar gyfer damcaniaethau mor wahanol â dadansoddi cymhlyg a mecaneg glasurol.

Mae'r canlynol yn rhai o'r cysyniadau pwysicaf mewn geometreg.

Gwirebau

 

Cymerodd Euclid agwedd haniaethol at geometreg yn ei Elfennau, un o'r llyfrau mwyaf dylanwadol a ysgrifennwyd erioed. Cyflwynodd rai wirebau, neu cynosodiadau, gan fynegi priodweddau sylfaenol, hunan-amlwg pwyntiau, llinellau a planau. Aeth ymlaen i dynnu priodweddau eraill yn drwyadl trwy resymu mathemategol. Un o nodweddion Euclid tuag at geometreg oedd ei drylwyredd, ac fe’i gelwir yn geometreg gwirebol neu synthetig. Ar ddechrau'r 19g, arweiniodd darganfyddiad o geometregau an-Ewclidaidd gan Nikolai Ivanovich Lobachevsky (1792-1856), János Bolyai (1802-1860), Carl Friedrich Gauss (1777-1855) ac eraill o ddiddordeb yn y ddisgyblaeth hon, ac yn yr 20g, defnyddiodd David Hilbert (1862–1943) ymresymu gwirebol mewn ymgais i ddarparu sylfaen fodern i geometreg.

Pwyntiau

Yn gyffredinol, ystyrir pwyntiau yn wrthrychau sylfaenol ar gyfer adeiladu geometreg. Gellir eu diffinio gan y priodweddau sydd ganddynt, fel yn niffiniad Euclid fel "yr hyn nad oes ganddo ran", neu mewn geometreg synthetig. Mewn mathemateg fodern, fe'u diffinnir yn gyffredinol fel elfennau o set o'r enw gofod, sydd ei hun wedi'i ddiffinio'n wirebol.

Gyda'r diffiniadau modern hyn, diffinnir pob siâp geometrig fel set o bwyntiau; nid yw hyn yn wir mewn geometreg synthetig, lle mae llinell yn wrthrych sylfaenol arall nad yw'n cael ei ystyried fel set y pwyntiau y mae'n mynd drwyddynt.

Llinellau

Mewn mathemateg fodern, o ystyried y llu o geometregau, mae'r cysyniad o linell wedi'i glymu'n agos â'r ffordd y disgrifir y geometreg. Er enghraifft, mewn geometreg ddadansoddol, diffinnir llinell yn y plân yn aml fel y set o bwyntiau y mae eu cyfesurynnau'n bodloni hafaliad llinol penodol, ond mewn lleoliad mwy haniaethol, fel geometreg mynychder, gall llinell fod yn wrthrych annibynnol, ar wahân i'r set o bwyntiau sydd arno. Mewn geometreg wahaniaethol, mae geodesig yn cyffredinoli'r syniad o linell i fannau crwm.

Planau

Mae'r plân yn arwyneb fflat, dau ddimensiwn sy'n ymestyn yr anfeidraidd ymhell. Plân yw'r analog dau ddimensiwn o bwynt (heb ddimensiwn), llinell (un dimensiwn) a lle (neu 'ofod') tri dimensiwn. Gall planau fodoli fel is-blanau (subspaces) hefyd, is-blanau o ryw ddimensiwn uwch, fel ystafell o fewn tŷ gada'i waliau'n cael eu hymestyn am byth, y tu allan i'r dyluniad. Dyma a wneir mewn geometreg Ewclidaidd.

Wrth weithio'n gyfan gwbl mewn gofod Ewclidaidd dau ddimensiwn, defnyddir y fannod (y plân), felly mae'r plân yn cyfeirio at y gofod cyfan. Mae llawer o dasgau sylfaenol mewn mathemateg, geometreg, trigonometreg, theori graff, a graffio yn cael eu gwneud mewn lle dau ddimensiwn, neu, mewn geiriau eraill, yn y plân.

Onglau

Y ffigur a ffurfir gan ddwy linell sy'n cwrdd ar fertig (cornel) yw ongl. Mae'r ongl hefyd yn fesuriad o gylchdroad, y gymhareb o hyd arc i'w radiws. Mesurir onglau yn aml mewn graddau (°), ond y radian yw'r uned safonol. Ceir 360° mewn un troad cylch, a 2π radian mewn un troad cylch. Gellir mesur onglau gydag onglydd. Defnyddir y llythyren Roeg theta (θ) fel symbol mathemategol am ongl.

 

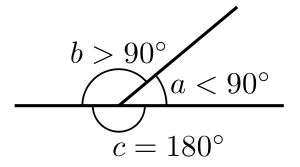
Mewn geometreg Ewclidaidd, defnyddir onglau i astudio polygonau a thrionglau, yn ogystal â ffurfio gwrthrych a asudir ar wahân. Mae astudio onglau triongl neu onglau mewn cylch yn sail i drigonometreg.

Cromliniau

Mae cromlin yn wrthrych 1 dimensiwn a all fod yn syth (fel llinell) ai peidio; gelwir cromliniau mewn gofod dau ddimensiwn yn gromliniau plân a gelwir y rhai mewn gofod 3 dimensiwn yn gromliniau gofod.

Arwynebau

 

Mae arwyneb yn wrthrych dau ddimensiwn, fel sffêr neu baraboloid. Mewn geometreg wahaniaethol a thopoleg, gan 'glytiau' (patches) dau ddimensiwn (neu gymdogaethau) sy'n cael eu cydosod gan differomorffiaethau neu homeomorffadau, yn y drefn honno. Mewn geometreg algebraidd, disgrifir arwynebau gan hafaliadau polynomial.

Felly, mewn geometreg solat, mae ochr (face) yn blân fflat, dau ddimensiwn, sy'n ffurfio rhan o ffin gwrthrych solat. Mae gan wrthrych solat tri dimensiwn sawl ochr, a gelwir y gwrthrych hwn yn bolyhedron e.e. mae'r ciwb yn bolyhedron ac mae ganddo 6 ochr. Mae gan bob ochr "arwyneb" (surface).

Maniffoldiau

Mae maniffold yn cyffredinoli'r cysyniadau o gromlin ac arwyneb. Mewn topoleg, mae maniffold yn ofod topolegol lle mae gan bob pwynt gymdogaeth sy'n homeomorffedd i ofod Ewclidaidd. Mewn geometreg wahaniaethol, mae maniffold gwahaniaethol yn ofod lle mae pob cymdogaeth yn wahanol i ofod Ewclidaidd.

Defnyddir maniffoldiau yn helaeth mewn ffiseg, gan gynnwys mewn perthnasedd cyffredinol a theori llinyn.

Hyd, arwynebedd, a chyfaint

Mae hyd, arwynebedd a chyfaint yn disgrifio maint neu faint gwrthrych mewn un dimensiwn, dau ddimensiwn, a thri dimensiwn.

Mewn geometreg Ewclidaidd a geometreg ddadansoddol, yn aml gellir cyfrifo hyd segment llinell gan y theorem Pythagorean .

Metrigau a mesurau

 

Gellir cyffredinoli'r cysyniad o hyd neu bellter, gan arwain at y syniad o fetrigau. Er enghraifft, mae'r metrig Ewclidaidd yn mesur y pellter rhwng pwyntiau yn y plân geometraidd, tra bod y metrig hyperbolig yn mesur y pellter yn y plân hyperbolig. Mae enghreifftiau pwysig eraill o fetrigau yn cynnwys metrig Lorentz perthnasedd arbennig a metrigau lled-Riemannian perthnasedd cyffredinol.

I gyfeiriad gwahanol, mae cysyniadau hyd, arwynebedd a chyfaint yn cael eu hymestyn gan theori mesur, sy'n astudio dulliau o neilltuo maint neu fesur i setiau, lle mae'r mesurau yn dilyn rheolau tebyg i rai arwynebedd a chyfaint glasurol.

Cyfathiant a chyflunedd

Mae cyfathiant a chyflunedd yn gysyniadau sy'n disgrifio pan fydd gan ddau siâp nodweddion tebyg. Mewn geometreg Ewclidaidd, defnyddir cyflunedd i ddisgrifio gwrthrychau sydd â'r un siâp, tra bod cyfathiant yn cael ei ddefnyddio i ddisgrifio gwrthrychau sydd yr un fath o ran maint a siâp. Roedd Hilbert, yn ei waith ar greu sylfaen fwy trylwyr ar gyfer geometreg, yn trin cyfathiant fel term heb ei ddiffinio y mae ei briodweddau wedi'u diffinio gan wirebau.

Lluniadau cwmpawd a llinellau syth

Roedd mathemategwyr geometraidd, clasurol yn canolbwyntio ar adeiladu gwrthrychau geometrig a oedd wedi'u disgrifio mewn rhyw ffordd arall. Yn glasurol, yr unig offerynnau a ganiateir mewn cystrawennau geometrig yw'r cwmpawd a'r pren mesur. Hefyd, roedd yn rhaid i bob lluniad fod yn gyflawn mewn nifer gyfyngedig o gamau. Fodd bynnag, roedd rhai problemau'n anodd neu'n amhosibl eu datrys trwy'r dulliau hyn yn unig, a darganfuwyd lluniadau dyfeisgar gan ddefnyddio parabolas a chromliniau eraill, yn ogystal â dyfeisiau mecanyddol.

Dimensiwn

 

Lle roedd y geometreg draddodiadol yn caniatáu dimensiynau 1 ( llinell), 2 (plân) a 3 (ein byd amgylchynol a genhedlwyd fel gofod tri dimensiwn), mae mathemategwyr a ffisegwyr wedi defnyddio dimensiynau uwch ers bron i ddwy ganrif. Un enghraifft o ddefnydd mathemategol ar gyfer dimensiynau uwch yw gofod cyfluniad (configuration space) o system real, sydd â dimensiwn sy'n hafal i 'raddfeydd o ryddid' y system. Er enghraifft, gall pum cyfesuryn ddisgrifio cyfluniad sgriw.

Mewn topoleg gyffredinol, mae'r cysyniad o ddimensiwn wedi'i ymestyn o rifau naturiol, i ddimensiwn anfeidrol ( e.e. gofodau Hilbert) a rhifau real, positif (mewn geometreg ffractal). Mewn geometreg algebraidd, mae dimensiwn yr amrywyn algebraidd (dimension of an algebraic variety) wedi derbyn nifer o ddiffiniadau sy'n ymddangos yn wahanol, sydd i gyd yn gyfwerth yn yr achosion mwyaf cyffredin.

Cymesuredd

 

Mewn cymesuredd, mae gwrthrych yn sefydlog i drawsnewidiad, megis adlewyrchiad, ond hefyd mathau eraill o drawsnewdiad. Ceir sawl math elfennol o gymersuredd gan gynnwys cymersuredd drwy: raddfa, adlewyrchiad, cylchdro a chymesuredd ffwythiannol. Ceir mathau gwahanol o gymesuredd hefyd mewn cerddoriaeth, iaith, gwrthrychau haniaethol, modelu mathemategol theori a hyd yn oed gwybodaeth. Gellir ei ganfod o fewn gwrthrychau pob dydd megis person, crisialau, cwilt ar wely, teils ar lawr, adeiladau, moleciwlau neu o fewn y byd natur ac o fewn gwrthrychau haniaethol megis fformiwlâu mathemategol. Mae thema cymesuredd mewn geometreg bron mor hen â gwyddoniaeth geometreg ei hun. Roedd gan siapiau cymesur fel y cylch, polygonau rheolaidd a solidau platonig arwyddocâd dwfn i lawer o athronwyr hynafol ac ymchwiliwyd iddynt yn fanwl cyn amser Euclid. Mae patrymau cymesur yn digwydd o ran eu natur ac fe'u rendrwyd yn artistig mewn llu o ffurfiau, gan gynnwys graffeg Leonardo da Vinci, MC Escher, ac eraill. Yn ail hanner y 19g, daeth y berthynas rhwng cymesuredd a geometreg o dan y chydd wydr. Cyhoeddodd rhaglen Erlangen Felix Klein fod cymesuredd, a fynegir trwy'r syniad o grŵp trawsnewid, mewn ystyr fanwl iawn, yn diffinio beth yw geometreg.

Mae cymesureddau arwahanol a pharhaus yn chwarae rolau amlwg mewn geometreg, y cyntaf mewn topoleg a theori grŵp geometrig, a'r ail mewn theori Lie a geometreg Riemannian.