Teorema De Pitágoras: Relação em geometria euclidiana entre os três lados de um triângulo retângulo

Na geometria euclidiana, o teorema afirma que:

Por definição, a hipotenusa é o lado oposto ao ângulo reto, e os catetos são os dois lados que o formam. O enunciado anterior relaciona comprimentos, mas o teorema também pode ser enunciado como uma relação entre áreas:

Para ambos os enunciados, pode-se equacionar

$${\displaystyle a^{2}=b^{2}+c^{2},}$$

O teorema de Pitágoras leva o nome do matemático grego Pitágoras (570 a.C. – 495 a.C.), que tradicionalmente é creditado pela sua descoberta e demonstração, embora seja frequentemente argumentado que o conhecimento do teorema seja anterior a ele (há muitas evidências de que matemáticos babilônicos conheciam algoritmos para calcular os lados em casos específicos, mas não se sabe se conheciam um algoritmo tão geral quanto o teorema de Pitágoras).

O teorema de Pitágoras é um caso particular da lei dos cossenos, do matemático persa Ghiyath al-Kashi (1380 – 1429), que permite o cálculo do comprimento do terceiro lado de qualquer triângulo, dados os comprimentos de dois lados e a medida de algum dos três ângulos.

 

Sendo c o comprimento da hipotenusa e a e b os comprimentos dos catetos, o teorema pode ser expresso por meio da seguinte equação:

$${\displaystyle c^{2}=a^{2}+b^{2}.}$$

 

Manipulando algebricamente essa equação, chega-se a que se os comprimentos de quaisquer dois lados do triângulo retângulo são conhecidos, o comprimento do terceiro lado pode ser calculado:

$${\displaystyle c={\sqrt {a^{2}+b^{2}}},b={\sqrt {c^{2}-a^{2}}}{\text{ e }}a={\sqrt {c^{2}-b^{2}}}.}$$

 

Outro corolário do teorema é que:

maior que qualquer um dos catetos pois todos os comprimentos são necessariamente números positivos, e c² > b², logo c > b, e c² > a², logo c > a. E a hipotenusa é menor que a soma dos catetos, pois c² = b² + a², e (b+a)² = b² + 2ba + a², logo c² < (b+a)², logo c < b + a.

Não se sabe ao certo qual seria a demonstração utilizada por Pitágoras. O teorema de Pitágoras já teve muitas demonstrações publicadas. O livro The Pythagorean Proposition, de Elisha Scott Loomis, por exemplo, contém 370 demonstrações diferentes. Há uma demonstração no livro Os Elementos, de Euclides. E também ofereceram demonstrações, o matemático indiano Bhaskara Akaria, o polímata italiano Leonardo da Vinci, e o vigésimo presidente dos Estados Unidos, James A. Garfield. O teorema de Pitágoras é tanto uma afirmação a respeito de áreas quanto a respeito de comprimentos, algumas provas do teorema são baseadas em uma dessas interpretações, e outras provas são baseadas na outra interpretação.

Por comparação de áreas

 

1. Desenha-se um quadrado de lado ${\displaystyle b+a;}$ 
2. De modo a subdividir este quadrado em quatro retângulos, sendo dois deles quadrados de lados, respectivamente, ${\displaystyle a}$  e ${\displaystyle b:}$  Traça-se dois segmentos de reta paralelos a dois lados consecutivos do quadrado, sendo cada um deles interno ao quadrado e com o mesmo comprimento que o lado do quadrado;
3. Divide-se cada um destes dois retângulos em dois triângulos retângulos, traçando-se as diagonais. Chama-se ${\displaystyle c}$  o comprimento de cada diagonal;
4. A área da região que resta ao retirar-se os quatro triângulos retângulos é igual a ${\displaystyle b^{2}+a^{2};}$ 
5. Desenha-se agora o mesmo quadrado de lado ${\displaystyle b+a,}$  mas coloca-se os quatro triângulos retângulos noutra posição dentro do quadrado: a posição que deixa desocupada uma região que é um quadrado de lado ${\displaystyle c.}$ 
6. Assim, a área da região formada quando os quatro triângulos retângulos são retirados é igual a ${\displaystyle c^{2}.}$ 

Como ${\displaystyle b^{2}+a^{2}}$  representa a área do quadrado maior subtraída da soma das áreas dos triângulos retângulos, e ${\displaystyle c^{2}}$  representa a mesma área, então ${\displaystyle b^{2}+a^{2}=c^{2}}$ . Ou seja: num triângulo retângulo o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.

Por semelhança de triângulos

 

Esta demonstração se baseia na proporcionalidade dos lados de dois triângulos semelhantes, isto é, que a razão entre quaisquer dois lados correspondentes de triângulos semelhantes é a mesma, independentemente do tamanho dos triângulos.

Sendo ABC um triângulo retângulo, com o ângulo reto localizado em C, como mostrado na figura. Desenha-se a altura com origem no ponto C, e chama-se H sua intersecção com o lado AB. O ponto H divide o comprimento da hipotenusa, c, nas partes d e e. O novo triângulo, ACH, é semelhante ao triângulo ABC, pois ambos tem um ângulo reto, e eles compartilham o ângulo em A, significando que o terceiro ângulo é o mesmo em ambos os triângulos também, marcado como θ na figura. Seguindo-se um raciocínio parecido, percebe-se que o triângulo CBH também é semelhante à ABC. A semelhança dos triângulos leva à igualdade das razões dos lados correspondentes:

$${\displaystyle {\frac {a}{c}}={\frac {e}{a}}}$$

 

$${\displaystyle {\frac {b}{c}}={\frac {d}{b}}.}$$

 

O primeiro resultado é igual ao cosseno de cada ângulo θ e o segundo resultado é igual ao seno.

Estas relações podem ser escritas como:

$${\displaystyle a^{2}=c\times e}$$

 

${\displaystyle b^{2}=c\times d.}$ 

$${\displaystyle a^{2}+b^{2}=c\times e+c\times d=c\times (d+e)=c^{2},}$$

 

$${\displaystyle a^{2}+b^{2}=c^{2}\ .}$$

 

Uma variante

Usando a mesma figura da demonstração acima, após ser mostrado que ΔABC, ΔACH e ΔCBH são semelhantes, pode-se demonstrar o teorema de Pitágoras usando-se o fato de que "a razão entre as áreas de triângulos semelhantes é igual ao quadrado da razão entre lados correspondentes", da seguinte forma: Chamando-se a área de ΔABC de x, a área de ΔACH é x*(b/c)², e a área de ΔCBH é x*(a/c)² (pois c, b e a são as hipotenusas de ΔABC, ΔACH e ΔCBH, respectivamente). Então, como a área do triângulo inteiro é a soma das áreas dos dois triângulos menores, tem-se x*(a/c)² + x*(b/c)² = x, então (a/c)² + (b/c)² = 1, então a² + b² = c².

Demonstração de Bhaskara

 

A análise da figura da direita permite computar a área do quadrado construído sobre a hipotenusa de um triângulo retângulo: ela é quatro vezes a área desse triângulo mais a área do quadrado restante, de lado (b−a). Equacionando-se, segue que:

$${\displaystyle c^{2}=4\cdot {\frac {ab}{2}}+(b-a)^{2}}$$

 

$${\displaystyle c^{2}=2ab+b^{2}-2ba+a^{2}}$$

 

$${\displaystyle c^{2}=b^{2}+a^{2}\ .}$$

 

Por cálculo diferencial

Pode-se chegar ao teorema de Pitágoras pelo estudo de como mudanças em um lado produzem mudanças na hipotenusa e usando um pouco de cálculo. É uma demonstração baseada na interpretação métrica do teorema, visto que usa comprimentos, não áreas.

 

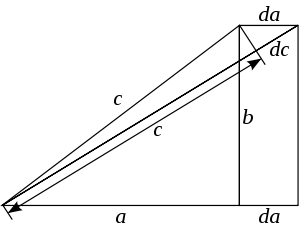
Como resultado da mudança da no lado a,

$${\displaystyle {\frac {da}{dc}}={\frac {c}{a}}}$$

 

por semelhança de triângulos e para mudanças diferenciais. Então,

$${\displaystyle c\,dc=a\,da}$$

 

por separação de variáveis.

que resulta da adição de um segundo termo para as mudanças no lado b.

Pela integração, segue:

$${\displaystyle c^{2}=a^{2}+\mathrm {constante} .}$$

 

Quando a = 0 então c = b, então a "constante" é b². Logo,

$${\displaystyle c^{2}=a^{2}+b^{2}.}$$

 

Num espaço com um produto interno

Pode-se estender o teorema de Pitágoras a espaços com produto interno e com uma norma induzida por este. Nessa situação:

$${\displaystyle \|x\|^{2}=\langle x,x\rangle .}$$

 

Dois vetores x e y são ditos perpendiculares se:

$${\displaystyle \langle x,y\rangle =\langle y,x\rangle =0.}$$

 

Segue então:

$${\displaystyle \|x+y\|^{2}=\langle x,x\rangle +\langle x,y\rangle +\langle y,x\rangle +\langle y,y\rangle =\|x\|^{2}+\|y\|^{2},}$$

 

que é o teorema de Pitágoras.

Pelo rearranjo das partes

 

 

Uma demonstração por rearranjo é dada pela animação à esquerda. Como a área total e as áreas dos triângulos são constantes, a área preta total é constante também. E a área preta pode ser dividida em quadrados delineados pelos lados a, b, c do triângulo, demonstrando que a² + b² = c².

Na animação à direita, um grande quadrado inicial é formado da área c ² tornando adjacentes quatro triângulos retângulos idênticos, deixando um pequeno quadrado no centro do grande quadrado, de modo a acomodar a diferença de comprimentos dos lados dos triângulos. Dois retângulos são formados, de lados a e b, movendo-se os triângulos. Incorporando o pequeno quadrado central com um destes retângulos, os dois retângulos são feitos em dois quadrados de áreas a ² e b ², mostrando que c ² = a ² + b ².

Demonstração de Euclides

 

A finalidade é mostrar que a área do quadrado AOMG é igual à área do quadrado AIHD e que BEFG é igual a BCHI, mostrando que o quadrado da hipotenusa é igual à soma do quadrado dos catetos. Veja que a reta definida por HL passa pelo centro do ângulo reto AGB e é ortogonal ao segmento AB. Temos que GL = AB, pois ambos são a hipotenusa do triângulo; e AB = HI, pois que ABCD é um quadrado. Logo GL=HI (o triângulo ABG é igual ao triângulo GML). Assim sendo, as áreas dos quadriláteros AIHD e ANLG são iguais, visto que tem a mesma base (HI = GL) e a mesma altura (AI). Mas temos que as áreas dos quadriláteros ANLG e AOMG são também iguais, pois que tem a base AG em comum e a mesma altura AO. Resulta que, pelo silogismo grego, se Y=Z e Z=W, então Y=W, em termo de área vale: AIHD = ANLG e ANLG = AOMG, então AIHD = AOMG.

Para mostrar que BEFG = BCHI segue-se de modo análogo.

Euclides mostra, desta forma puramente geométrica, que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.

 

A recíproca do teorema de Pitágoras também é verdadeira:

"Para qualquer triângulo com lados l, m, e r, se l² + m² = r², então o ângulo entre l e m mede 90°".

ou, usando apenas palavras,

Ela pode ser provada usando-se a lei dos cossenos.

Talvez nenhuma outra relação geométrica seja tão utilizada em matemática como o teorema de Pitágoras. Na geometria cartesiana, muito usada em ciências e engenharia, todos os cálculos que envolvem relações espaciais e trigonometria têm como base este teorema. É possível utilizar o teorema de Pitágoras em todos os polígonos, pois eles podem ser divididos em triângulos e esses em triângulos retângulos. E por extensão, em todos os poliedros.

A diagonal do quadrado

 

A diagonal do quadrado divide-o em dois triângulos retângulos congruentes. Sendo ${\displaystyle l}$  o lado e ${\displaystyle d}$  a diagonal, segue que:

$${\displaystyle d^{2}=l^{2}+l^{2}=2\,l^{2}.}$$

 

$${\displaystyle d={\sqrt {2\,l^{2}}}=l{\sqrt {2}}.}$$

 

A altura do triângulo equilátero

 

A altura do triângulo equilátero divide-o em dois triângulos retângulos congruentes. Sendo ${\displaystyle l}$  o lado e ${\displaystyle h}$  a altura, segue que:

$${\displaystyle l^{2}=h^{2}+\left({\frac {l}{2}}\right)^{2}=h^{2}+{\frac {l^{2}}{4}}}$$

 

$${\displaystyle h^{2}={\frac {3\,l^{2}}{4}}.}$$

 

Finalmente, a altura do triângulo equilátero é encontrada como:

$${\displaystyle h={\sqrt {\frac {3\,l^{2}}{4}}}={\frac {l{\sqrt {3}}}{2}}.}$$

 

A diagonal do cubo

 

Seja a a medida da aresta de um cubo (isto é, a medida de um lado de uma das faces quadradas), pelo teorema de Pitágoras:

$${\displaystyle AC^{2}=a^{2}+a^{2}.}$$

 

$${\displaystyle AC'^{2}=a^{2}+AC^{2}.}$$

 

De I e II:

$${\displaystyle AC'^{2}=a^{2}+a^{2}+a^{2}.}$$

 

$${\displaystyle AC'={\sqrt {3a^{2}}}=a{\sqrt {3}}.}$$

 

Nas geometrias n-dimensionais, por raciocínio análogo pode-se obter pelo teorema de Pitágoras os valores das diagonais do hipercubo unitário em função de sua respectiva dimensão: As diagonais de quadrado, cubo, tesserato e n-cubo unitários medem, respectivamente, ${\displaystyle {\sqrt {2}},}$  ${\displaystyle {\sqrt {3}},}$  ${\displaystyle {\sqrt {4}}}$  (ou seja, 2) e ${\displaystyle {\sqrt {n}}.}$ 

Identidade trigonométrica fundamental

 Ver artigo principal: Identidade trigonométrica fundamental

 

$${\displaystyle \mathrm {sen} \,\theta ={\frac {b}{c}},\quad \cos \theta ={\frac {a}{c}}.}$$

 

$${\displaystyle {\cos }^{2}\theta +{\mathrm {sen} \,}^{2}\theta ={\frac {a^{2}+b^{2}}{c^{2}}}=1,}$$

 

Ternos pitagóricos

 Ver artigo principal: Terno pitagórico

Um terno pitagórico (trio pitagórico) consiste em três números inteiros positivos a, b, e c, tais que a ² + b ² = c ². Em outras palavras, um terno pitagórico representa os comprimentos dos lados de um triângulo retângulo, onde todos os três lados têm comprimentos inteiros. Essa tripla é geralmente escrita como (a, b, c ). Alguns exemplos bem conhecidos são (3, 4, 5) e (5, 12, 13).

Um terno pitagórico primitivo é aquele em que a, b e c são coprimos (o máximo divisor comum de a, b e c é 1).

Lista de ternos pitagóricos primitivos até 100:

(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)

A incomensurabilidade

 Ver artigo principal: Número irracional

Pitágoras sabia na época, entretanto, que seu teorema tinha uma falha: Quando os catetos do triângulo eram iguais, seu teorema não funcionava, pois não haveria uma medida racional para a hipotenusa. Conta a História que a primeira atitude de Pitágoras frente a essa incoerência na matemática foi a de esconder tal fato. Matemáticos e geômetras que o sucederam desde aquela época tentavam compreender o porquê da incomensurabilidade – os lados do triângulo não tinham medida em comum, ou seja, não podiam ser medidos de forma exata através de uma unidade comum a ambos.

Com efeito, suponha que seja a hipotenusa p e que os catetos sejam iguais e representados pela letra q. Sabe-se que p / q é uma fração irredutível (se não fosse torná-la-íamos, até que não mais pudéssemos, restando um numerador par e um denominador ímpar, ou vice-versa). Da aplicação do teorema resulta p² = 2q². Obviamente p² é par, pois é o dobro de q², ou seja, vem de um produto de um número multiplicado por 2. Se p² é par, implica que p é par (o quadrado de um número par é sempre número par e o quadrado de um número ímpar é sempre número ímpar), logo q obrigatoriamente deve ser ímpar, senão a fração dada acima não seria irredutível. Fazendo agora p = 2k (o que pode ser feito, pois p é par) reescrevemos: (2k)² = 2q² simplificando resulta 4k² = 2q² que resulta 2k² = q², o que quer dizer, pelo mesmo raciocínio anterior, que q é par, o que é absurdo pois antes resultou ser ímpar. Um número não pode ser par e ímpar ao mesmo tempo.

A solução só veio 25 séculos depois, no século XIX, com Dedekind quando foi necessária cortar a reta dos números racionais e introduzir o conjunto dos números irracionais para suprir essa deficiência da Matemática.

 

Uma das consequências do teorema de Pitágoras é que comprimentos incomensuráveis (ou seja, cuja razão é um número irracional, tal como a raiz quadrada de 2), podem ser construídos, com instrumentos como régua e compasso. Um triângulo retângulo com ambos os catetos de medida unitária tem uma hipotenusa de comprimento igual à raiz quadrada de 2. A figura da direita mostra como construir segmentos de reta com comprimentos iguais à raiz quadrada de qualquer número inteiro positivo.

Valor de pi

 Ver artigo principal: pi

 

Em Sobre as Medidas do Círculo, Arquimedes utilizou o teorema de Pitágoras para calcular uma aproximação para o valor do número pi. Ele fez isso posicionando um hexágono regular circunscrito a um círculo e um hexágono regular menor inscrito no círculo, e então realizando a progressiva duplicação do número de lados de cada polígono regular assim obtido, cujo perímetro em cada nova etapa ele calculava por meio do teorema de Pitágoras.

Distância entre dois pontos

 Ver artigo principal: Geometria analítica

O teorema de Pitágoras pode ser traduzido para a linguagem das coordenadas de Descartes:

Seja ${\displaystyle A=(x_{1},y_{1})}$  e ${\displaystyle B=(x_{2},y_{2}).}$  Para auxiliar, seja ${\displaystyle C=(x_{2},y_{1}).}$ 

Como A e C possuem mesma ordenada, ${\displaystyle d(A,C)=\left|x_{1}-x_{2}\right|.}$ 

Como B e C possuem mesma abcissa, ${\displaystyle d(B,C)=\left|y_{1}-y_{2}\right|}$ 

Então ${\displaystyle d(A,B)={\sqrt[{}]{d(A,C)^{2}+d(B,C)^{2}}}={\sqrt[{}]{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}.}$ 

Lei dos cossenos

 Ver artigo principal: Lei dos cossenos

O teorema de Pitágoras permite calcular um lado de um triângulo retângulo conhecendo os outros dois. A lei dos cossenos permite calculá-lo em qualquer triângulo. Assim, o teorema de Pitágoras é um caso especial do teorema mais geral que relaciona o comprimento dos lados de qualquer triângulo, a lei dos cossenos é a seguinte:

$${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos {\theta },}$$

 

Teorema de Gua

 Ver artigo principal: Teorema de Gua

 

O teorema de Pitágoras pode ser generalizado para um n-simplex retângulo: o quadrado do (n-1)-volume da hipotenusa é igual à soma dos quadrados dos (n-1)-volumes dos catetos. Em particular, num tetraedro retângulo (isto é, que tem três faces perpendiculares entre si - os "catetos"), o quadrado da área da "hipotenusa" (a face que não é perpendicular às restantes) é igual à soma dos quadrados das áreas dos catetos.

Figuras semelhantes nos três lados

 

O teorema de Pitágoras foi generalizado por Euclides em seu livro Os Elementos para estender-se além das áreas dos quadrados nos três lados, para figuras semelhantes:

Outro matemático que demonstrou essa afirmação foi George Pólya, e o resultado ficou conhecido como Generalização do Teorema de Pitágoras que diz:

Se C, A e B são três figuras semelhantes, construídas, respectivamente, sobre a hipotenusa e os catetos do triângulo retângulo, então as áreas das figuras A, B e C satisfazem a relação A(C) = A(A) + A(B) (Podemos observar essa figura ao lado).

Demonstração: Usaremos o resultado que garante que se duas figuras X e X' são semelhantes com razão de semelhança ${\displaystyle K\in \mathbb {R} }$ , então ${\displaystyle A(X)/A(X')=K^{2}}$ . Como as figuras A, B e C são semelhantes, temos que

${\displaystyle {\frac {A(A)}{A(C)}}=\left({\frac {a}{c}}\right)^{2}={\frac {a^{2}}{c^{2}}}\,\,\,e\,\,\,{\frac {A(B)}{A(C)}}=\left({\frac {b}{c}}\right)^{2}={\frac {b^{2}}{c^{2}}}}$ 

Daí, obtemos

${\displaystyle {\frac {A(A)+A(B)}{A(C)}}={\frac {a^{2}+b^{2}}{c^{2}}}}$ 

e como o triângulo é retângulo, pelo Teorema de Pitágoras, temos que ${\displaystyle c^{2}=a^{2}+b^{2}}$ , substituindo na equação anterior, encontramos

${\displaystyle {\frac {A(A)+A(B)}{A(C)}}={\frac {c^{2}}{c^{2}}}=1\Rightarrow A(C)=A(A)+A(B)}$ 

 

 

O teorema de Pitágoras é derivado dos axiomas da geometria euclidiana, por isso, acreditava-se que a versão euclidiana não fosse válida nas geometrias não euclidianas. (Foi mostrado que o teorema de Pitágoras é equivalente ao postulado das paralelas, que por sua vez, é equivalente à afirmação de que "a soma dos ângulos internos de um triângulo é igual a dois ângulos retos", usada em todas as demonstrações apresentadas do teorema). Em outras palavras, numa geometria não euclidiana, a relação entre os lados de um triângulo deveria necessariamente tomar outra forma. Por exemplo, na geometria esférica, a² + b² ≠ c².

Seja c a hipotenusa de um triângulo retângulo numa geometria não euclidiana e a e b os catetos. O teorema de Pitágoras toma uma das seguintes formas:

• Na geometria esférica, tem-se
  ${\displaystyle \cos(c)=\cos(a)\cos(b).}$ 
• Na geometria hiperbólica tem-se
  ${\displaystyle \cosh(c)=\cosh(a)\cosh(b).}$ 

Entretanto, existe uma versão para a geometria hiperbólica (usando uma métrica adequada) na qual o teorema apresenta-se no formato conhecido.

Quanto aos espaços vetoriais, em alguns deles o teorema de Pitágoras (ou mesmo generalizações dele) é verdadeiro e em outros ele é falso. Sabe-se, por exemplo, que o teorema de Pitágoras é verdadeiro em espaços pré-hilbertianos. Erhard Schmidt provou o teorema de Pitágoras para espaços vetoriais abstratos com produto interno. Dieter Brill e Ted Jacobson derivaram o análogo do teorema de Pitágoras no espaço minkowskiano (que chamaram de "Teorema de Pitágoras para o espaço-tempo").

Embora o teorema de Pitágoras seja necessariamente falso em qualquer espaço descontínuo, Jean Paul Van Bendegem mostrou que num espaço desse tipo o teorema de Pitágoras pode ser usado como aproximação dentro de certos limites de tolerância.

O teorema de Pitágoras também foi generalizado para as geometrias riemannianas. Investigações nesse tema remontam ao próprio Bernhard Riemann, e a questão acerca da validade do teorema de Pitágoras na vizinhança de um ponto foi abordada por, dentre outros, Hermann von Helmholtz, Sophus Lie e Hermann Weyl.

 

 

O teorema de Pitágoras foi descoberto independentemente nas antigas civilizações babilônica, indiana, chinesa e grega.

A história do teorema pode ser dividida em quatro partes: o conhecimento de trios pitagóricos, conhecimento da relação entre os lados de um triângulo retângulo, conhecimento das relações entre ângulos adjacentes, e demonstrações do teorema dentro de sistemas dedutivos.

Egito

O historiador da matemática alemão Moritz Cantor, tomando por base que 3² + 4² = 5² era conhecido dos egípcios e que eles usavam cordas em agrimensura, especulou que eles construíam ângulos retos por meio de uma corda com nós para formar um triângulo de lados 3, 4 e 5. Bartel van der Waerden afirmou que não há evidências que sustentem esta especulação, visão compartilhada por Thomas Little Heath.

Mesopotâmia

Há provas que os antigos babilônios já conheciam o teorema muito antes de Pitágoras. Tabletes de barro do período de 1800 a.C. a 1600 a.C. foram encontrados e estudados, estando hoje em vários museus. Um deles, Plimpton 322, mostra uma tabela de 15 linhas e 3 colunas, ilustrando trios pitagóricos.

Índia

Na Índia, o Sulba Sutra escrito por Baudhayana em data incerta entre os séculos VIII a.C. e II a.C., contém uma lista de trios pitagóricos descobertos algebricamente, um enunciado do teorema de Pitágoras, e uma demostração geométrica deste para um triângulo retângulo isósceles. O Sulba Sutra de Apastamba (ca. 600 a.C.) contém uma demostração numérica do caso geral do teorema de Pitágoras, usando cálculo de áreas. Van der Waerden acreditava que esta demostração "estava certamente baseada em tradições antigas". Carl Benjamin Boyer pensava que os elementos achados em Śulba-sũtram deviam ter raízes mesopotâmicas.

China

Na China, o teorema também já era conhecido cerca de 600 anos antes do período Pitagórico. O problema "Gou Gu", do famoso livro chinês Zhoubi Saunjing é uma evidência da existência de conhecimento a respeito do teorema.

Grécia

Pitágoras (569 a.C. - 475 a.C.) usou métodos algébricos para construir trios pitagóricos, de acordo com os comentários de Proclo sobre Euclides. Proclo, porém, escreveu entre os anos 410 e 485 d.C. Segundo Thomas Little Heath (1861–1940), não existe nenhuma atribuição específica do teorema a Pitágoras na literatura grega que se conserva dos cinco séculos posteriores à época em que Pitágoras viveu. No entanto, quando autores como Plutarco e Cícero atribuíram o teorema a Pitágoras, fizeram-no de tal forma que sugeria que esta atribuição era amplamente conhecida e livre de qualquer dúvida. "Se esta fórmula é corretamente atribuída ao próprio Pitágoras, [...] pode-se assumir com certeza que pertence ao período mais antigo da matemática pitagórica".

Segundo Proclo, por volta do ano 400 a.C. Platão forneceu um método para encontrar trios pitagóricos que combinava álgebra e geometria. A demonstração axiomática do teorema mais antiga que se conhece aparece nos Elementos de Euclides, que data aproximadamente do ano 300 a.C.

Álgebra Lista de construções do desenho geométrico Perpendicularidade Teorema Terno pitagórico Triângulo Trigonometria

Área Geometria Mosaico pitagórico Número irracional Regra do paralelogramo Teorema de Tales Terno pitagórico Último teorema de Fermat

O wikilivro Matemática elementar tem uma página sobre Triângulo retângulo   O Commons possui uma categoria com imagens e outros ficheiros sobre Teorema de Pitágoras

Referências

Ligações externas

• Demonstração do teorema de Pitágoras (segundo Euclides)
• «Pythagorean Theorem and its many proofs» (em inglês). O teorema de Pitágoras e suas muitas demonstrações, no Cut-the-Knot. 
• Geometria Analítica e Desenho Geométrico, Unicamp: Teorema de Pitágoras Introdução, a demonstração de Da Vinci, e História do teorema.

•   Portal da matemática