Vector: Obxecto xeométrico que ten magnitude (ou lonxitude) e dirección

Os vectores utilízanse para describir magnitudes vectoriais tales como velocidades, aceleracións ou forzas, nas cales é importante considerar non só o valor senón tamén a dirección e máis o sentido.

Aínda que frecuentemente se describa a un vector por un número de "compoñentes", cada un deles dependente do sistema de coordenadas particular que se use, as propiedades dun vector non dependen do sistema de coordenadas usado para o describir.

Un exemplo común dun vector é a forza. Ten un valor e unha orientación en tres dimensións (a diferenza de moitas dimensións espaciais, que teñen dúas), e a suma múltipla das forzas de acordo coa lei do paralelogramo.

En matemáticas, un vector é un elemento dunha estrutura alxébrica chamada espazo vectorial, que esencialmente é un conxunto de elementos cun conxunto de axiomas que debe satisfacer cada un deles.

Matematicamente un vector pode ser tamén un conxunto de elementos ordenados entre si mais, a diferenza dun conxunto normal como o dos números naturais, neste caso o conxunto está ordenado.

Represéntase por un segmento orientado para denotar o seu sentido (o da frecha), a súa magnitude (a lonxitude da frecha) e mais o punto de onde parte. Para este tipo de vectores (xeralmente bi ou tridimensionais) defínense módulo, dirección e sentido.

 

Os eixos do sistema de coordenadas descríbense xeralmente empregando as letras x, y e z, xeramente o eixo z representa o perpendicular ao plano. Os vectores pódense representar con letras, cunha frecha enriba (${\displaystyle {\vec {a}}}$ ), ou simplemente en letra grosa (${\displaystyle \mathbf {a} }$ ). As coordenadas ou compoñentes dun vector nun sistema de referencia poden escribirse entre parénteses e separadas con comas:

${\displaystyle {\vec {a}}=(a_{1},a_{2},a_{3},...,a_{n})}$ .

No espazo vectorial de tres dimensións empréganse tres compoñentes:

${\displaystyle {\vec {a}}=(a_{x},a_{y},a_{z})}$ .

Outro xeito típico de anotar un vector nas tres dimensións é definilo como a combinación dos vectores unitarios cartesianos i, j e k:

${\displaystyle {\vec {a}}=a_{x}\,{\vec {i}}+a_{y}\,{\vec {j}}+a_{z}\,{\vec {k}}}$ 

Un vector ten as seguintes propiedades:

- Punto de aplicación, é a orixe do vector.

- Módulo, expresa o valor numérico da magnitude vectorial. Represéntase pola lonxitude do segmento, sempre en valor absoluto. Por exemplo, se se quere expresar que o módulo de ${\displaystyle {\vec {a}}}$  vale 5 unidades, faise así: ${\displaystyle |{\vec {a}}|=5u}$ . Expresado con fórmulas, dado un vector ${\displaystyle {\vec {a}}}$  de coordenadas ${\displaystyle (a_{x},a_{y},a_{z})}$  o seu módulo é ${\displaystyle |{\vec {a}}|={\sqrt {a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}}$ .

- Dirección, que é a da recta soporte, que se expresa matematicamente cunha ecuación de recta, que se lle chama liña de acción.

- Sentido, distinguíndose dous sentidos sobre a recta de aplicación do vector, graficamente, a punta da frechiña.

Clasificación dos vectores

Segundo o seu punto de aplicación:

- Vector fixo, que ten un punto de aplicación definitorio, do que non se despraza.

- Vectores deslizantes, o seu punto de aplicación pode estar en calquera punto dunha recta soporte definida.

- Vector libre, non ten relevancia o seu punto de aplicación.

Outros vectores significantes:

- Vector unitario, un vector cuxo módulo é unha unidade, que se calcula: ${\displaystyle {\vec {u_{a}}}={\frac {(a_{x},a_{y},a_{z})}{|{\vec {a}}|}}}$ . Os vectores unitarios correspondentes a (1,0,0), (0,1,0) e (0,0,1) denomínanse ${\displaystyle {\hat {\imath }}}$ , ${\displaystyle {\hat {\jmath }}}$  e ${\displaystyle {\hat {k}}}$ , sendo ${\displaystyle {\hat {\imath }}}$  o vector unitario do eixe do x, ${\displaystyle {\hat {\jmath }}}$  o vector unitario do eixo y, e ${\displaystyle {\hat {k}}}$  o do z.

- Vector oposto a outro é o que ten o mesmo punto de aplicación, módulo e dirección mais sentido contrario. Así o vector oposto a ${\displaystyle {\vec {a}}}$  é ${\displaystyle -{\vec {a}}}$ .

- Vectores equipolentes, vectores con igual módulo e sentido, e rectas soporte paralelas e, entón, tamén distintos puntos de aplicación.

- Vectores paralelos, que teñen coordenadas proporcionais entre si (equipolentes con distinto módulo, por exemplo).

- Vectores concorrentes, cando teñen o mesmo punto de aplicación, no caso de vectores fixos, ou cando simplemente teñen un punto en común (punto de concorrencia).

- Vectores coplanares, todos os vectores están contidos no mesmo plano.

- Vectores colineares, que comparten unha mesma recta de acción

 

 

Método gráfico

A suma e resta de vectores ten en conta, ademais da magnitude escalar ou módulo, o sentido das magnitudes intervenientes. Nas figuras achegadas nesta páxina esquematízase o método gráfico para buscar o resultado.

Método do paralelogramo

Consiste en pór graficamente os dous vectores de xeito que as respectivas orixes coincidan nun punto, completando o resto do paralelogramo por paralelas. O resultado da suma é a diagonal de dito paralelogramo.

Método do triángulo

Consiste en poñer graficamente un vector a continuación doutro, facendo coincidir o extremo inicial dun vector co extremo final do outro vector. O vector suma resultante forma un triángulo canda estes dous vectores, que corresponde ao lado oposto ao vértice dos vectores colocados correctamente, ou dito doutro xeito, vai dende a orixe dun vector até a fin do outro (a e b respectivamente no debuxo adxacente)

Método analítico

• A suma

Con dous vectores de coordenadas,

${\displaystyle {\vec {a}}=(a_{x},a_{y},a_{z})}$ 

${\displaystyle {\vec {b}}=(b_{x},b_{y},b_{z})}$ 

o resultado da suma é:

${\displaystyle {\vec {a}}+{\vec {b}}=[(a_{x}+b_{x}),(a_{y}+b_{y}),(a_{z}+b_{z})]}$ 

• A resta

Para restar dous vectores libres ${\displaystyle {\vec {a}}}$  e ${\displaystyle {\vec {b}}}$  súmase ${\displaystyle {\vec {a}}}$  co oposto de ${\displaystyle {\vec {b}}}$ :

${\displaystyle {\vec {a}}-{\vec {b}}={\vec {a}}+(-{\vec {b}})}$ 

O resultado da resta é:

${\displaystyle {\vec {a}}-{\vec {b}}=[(a_{x}-b_{x}),(a_{y}-b_{y}),(a_{z}-b_{z})]}$ 

Módulo resultante

Dados dous vectores ${\displaystyle {\vec {a}}}$  e ${\displaystyle {\vec {b}}}$ , de módulos coñecidos e que forman o ángulo ${\displaystyle \theta }$  entre si, pódese obter o módulo ${\displaystyle \left|{\vec {a}}+{\vec {b}}\right|}$  coa seguinte fórmula:

${\displaystyle \left|{\vec {a}}+{\vec {b}}\right|={\sqrt {\left.|{\vec {a}}\right|^{2}+\left|{\vec {b}}\right|^{2}+2|{\vec {a}}|\left|{\vec {b}}\right|\cos \theta }}}$ 

Dedución da expresión

Sexan dous vectores ${\displaystyle {\vec {a}}}$  e ${\displaystyle {\vec {b}}}$  que forman un ángulo ${\displaystyle \theta }$  entre si:

 

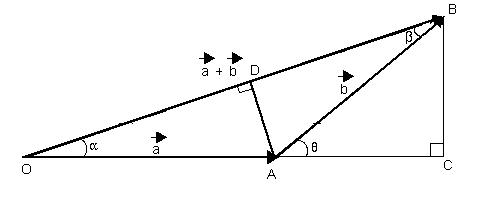
A fórmula para calcular ${\displaystyle \left|{\vec {a}}+{\vec {b}}\right|}$  dedúcese observando os triángulos rectángulos que se forman, OCB e ACB, e aplicando o Teorema de Pitágoras. No triángulo OCB:

${\displaystyle OB^{2}=OC^{2}+CB^{2}}$ 

${\displaystyle OB=|{\vec {a}}+{\vec {b}}|}$ 

${\displaystyle OC=\left|{\vec {a}}\left|+AC\right.\right.}$ 

Resultando:

${\displaystyle \left|{\vec {a}}+{\vec {b}}\right|^{2}=\left(|{\vec {a}}|+AC\right)^{2}+CB^{2}}$ 

No triángulo ACB :

${\displaystyle {\frac {AC}{|{\vec {b}}|}}=\cos \theta }$ 

${\displaystyle AC=|{\vec {b}}|\cos \theta }$ 

${\displaystyle {\frac {CB}{|{\vec {b}}|}}=sen\theta }$ 

${\displaystyle CB=|{\vec {b}}|sen\theta }$ 

Substituíndo isto na igualdade de antes resulta:

${\displaystyle \left|{\vec {a}}+{\vec {b}}\right|^{2}=\left(|{\vec {a}}|+|{\vec {b}}|\cos \theta \right)^{2}+\left(\left|{\vec {b}}|sen\theta \right)^{2}\right.}$ 

${\displaystyle \left.\left|{\vec {a}}+{\vec {b}}\right|^{2}=|{\vec {a}}|^{2}+2|{\vec {a}}||{\vec {b}}\right|\cos \theta +\left|{\vec {b}}\right|^{2}\cos ^{2}\theta +\left|{\vec {b}}\right|^{2}sen^{2}\theta }$ 

${\displaystyle \left.\left|{\vec {a}}+{\vec {b}}\right|^{2}=|{\vec {a}}|^{2}+2|{\vec {a}}||{\vec {b}}\right|\cos \theta +\left|{\vec {b}}\right|^{2}\left(\cos ^{2}\theta +sen^{2}\theta \right)}$ 

${\displaystyle \left.\cos ^{2}\theta +sen^{2}\theta =1\rightarrow \left|{\vec {a}}+{\vec {b}}\right|^{2}=|{\vec {a}}|^{2}+2|{\vec {a}}||{\vec {b}}\right|\cos \theta +\left|{\vec {b}}\right|^{2}}$ 

${\displaystyle \left|{\vec {a}}+{\vec {b}}\right|={\sqrt {\left.|{\vec {a}}|^{2}+2|{\vec {a}}||{\vec {b}}\right|\cos \theta +\left|{\vec {b}}\right|^{2}}}}$ 

${\displaystyle \left|{\vec {a}}+{\vec {b}}\right|={\sqrt {\left.|{\vec {a}}|^{2}+\left|{\vec {b}}\right|^{2}+2|{\vec {a}}||{\vec {b}}\right|\cos \theta }}}$ 

Obtención da Dirección

Para obter os ángulos ${\displaystyle \alpha ,\beta }$  directores no anterior exemplo temos que coñecer o ángulo ${\displaystyle \theta }$  e ter calculado ${\displaystyle \left|{\vec {a}}+{\vec {b}}\right|}$  .

Podemos usar esta fórmula:

${\displaystyle {\frac {|{\vec {b}}|}{sen\alpha }}={\frac {|{\vec {a}}|}{sen\beta }}={\frac {\left|{\vec {a}}+{\vec {b}}\right|}{sen\theta }}}$ 

Coa fórmula obteremos os seos, despois para achar o ángulo a partir do seo temos que ter en conta que:

${\displaystyle \alpha +\beta =\theta }$ 

 

O produto dun vector cun escalar é outro vector que conserva a dirección orixinal, o seu módulo é o produto do escalar polo módulo do vector e o sentido é o mesmo ou oposto segundo o escalar sexa positivo ou negativo respectivamente.

Graficamente sería poñer, sobre a mesma recta da dirección, o módulo tantas veces como marque o escalar, e de ser negativo, viralo sentido do vector (mire o debuxo).

Analiticamente, un número ${\displaystyle n\,}$  e un vector ${\displaystyle {\vec {a}}}$ , o produto ${\displaystyle n\,{\vec {a}}}$  realízase multiplicando cada unha das compoñentes do vector polo escalar. Dado o vector de tres compoñente

${\displaystyle {\vec {a}}=(a_{x},a_{y},a_{z})}$ 

o seu produto polo escalar é

${\displaystyle n\,\mathbf {a} =(na_{x},na_{y},na_{z})}$ 

é dicir, multiplícase por ${\displaystyle n\,}$  cada unha das compoñentes do vector.

Dados os vectores ${\displaystyle {\vec {a}}=(a_{x},a_{y},a_{z})}$  e ${\displaystyle {\vec {b}}=(b_{x},b_{y},b_{z})}$ , o ángulo ${\displaystyle \theta }$  calcúlase polo seu coseno:

${\displaystyle cos\theta ={\frac {a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}}{|{\vec {a}}||{\vec {b}}|}}}$ 

Isto deriva do produto escalar.

Artigo principal: Produto escalar.

 

${\displaystyle \mathbf {A} \cdot \mathbf {B} =|\mathbf {A} ||\mathbf {B} |\cos \theta =A\,B\,\cos \theta }$ 

${\displaystyle |\mathbf {A} \times \mathbf {B} |=|\mathbf {A} ||\mathbf {B} |\sin \theta =A\,B\,\sin \theta }$ 

Outros artigos

• Escalar
• Espazo vectorial
• Cálculo vectorial

Ligazóns externas

• Xoga con vectores
• Suma e resta de vectores (en castelán)