Vector

Vector
concepto geométrico (es)
vector (es)

En matemátiques defínese un vector como un elementu d'un espaciu vectorial. Esta noción ye más astracta y pa munchos espacios vectoriales nun ye posible representar los sos vectores por aciu el módulu y la direición. En particular los espacios de dimensión infinita ensin productu angular nun son representables d'esa manera. Los vectores nun espaciu euclideu pueden representase geométricamente como segmentos de recta ${\displaystyle \mathbb {R} }$, nel planu ${\displaystyle \mathbb {R} ^{2}}$ (bidimensional), o nel espaciu ${\displaystyle \mathbb {R} ^{3}}$ (tridimensional).

Dellos exemplos de magnitúes físiques que son magnitúes vectoriales: la velocidá con que se mueve un móvil, yá que nun queda definida tan solo pol so módulu que ye lo que marca'l velocímetru, nel casu d'un automóvil, sinón que se riquir indicar la direición (escontra onde se dirixe), la fuercia qu'actúa sobre un oxetu, yá que el so efeutu depende amás de la so magnitú o módulu, de la direición na qu'actúa; tamién, el desplazamientu d'un oxetu, pos ye necesariu definir el puntu inicial y final del movimientu.

Esta seición esplica los aspeutos básicos, la necesidá de los vectores pa representar ciertes magnitúes físiques, los componentes d'un vector, la notación de los mesmos, etc.

Definición

 

Llámase vector de dimensión ${\displaystyle n\,}$  a una tupla de ${\displaystyle n\,}$  númberos reales (que se llamen componentes del vector). El conxuntu de tolos vectores de dimensión ${\displaystyle n\,}$  represéntase como ${\displaystyle \mathbb {R} ^{n}}$  (formáu por aciu el productu cartesianu).

Asina, un vector ${\displaystyle \scriptstyle v}$  perteneciente a un espaciu ${\displaystyle \mathbb {R} ^{n}}$  represéntase como:

${\displaystyle v=(a_{1},a_{2},a_{3},\dots ,a_{n})}$ , onde ${\displaystyle v\in \mathbb {R} ^{n}}$ 

Un vector tamién puede vese dende'l puntu de vista de la xeometría como vector xeométricu (usando frecuentemente l'espaciu tridimensional ${\displaystyle \mathbb {R} ^{3}}$  o bidimensional ${\displaystyle \mathbb {R} ^{2}}$ ).

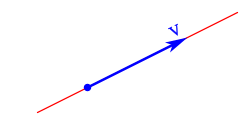
Un vector fixu del planu euclídeo ye un segmentu empobináu, nel qu'hai qu'estremar trés carauterístiques:

• Módulu: el llargor del segmentu.
• Direición: la direición de la recta.
• Sentíu: la orientación del segmentu, del orixe al estremu del vector.

N'inglés, la pallabra direction indica tantu la direición como'l sentíu del vector, colo que se define'l vector con solu dos carauterístiques: módulu y direición.

Los vectores fixos del planu se denotan con dos lletres mayúscules (y una flecha escontra la derecha enriba), por casu ${\displaystyle {\overrightarrow {AB}}}$ , qu'indiquen el so orixe y estremu respeutivamente. Esto ye, el puntu A ye l'orixe o puntu d'aplicación y el puntu B ye l'estremu del vector ${\displaystyle {\overrightarrow {AB}}}$ , que les sos coordenaes son:

${\displaystyle {\overrightarrow {AB}}=(x_{B}-x_{A},y_{B}-y_{A})\,}$ 

Carauterístiques d'un vector

 

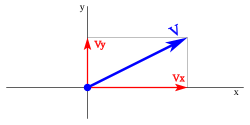
Un vector puede definise polos sos coordenaes, si'l vector ta nel planu xy, represéntase:

${\textstyle {\vec {V}}={\boldsymbol {V}}=(V_{x},V_{y})}$ 

siendo les sos coordenaes:

${\displaystyle V_{x},\;V_{y}}$ 

Si consideramos el triángulu formáu polos componentes ${\displaystyle V_{x},V_{y}}$  (como catetos) y ${\displaystyle V}$  (como hipotenusa): puede calculase ${\displaystyle V_{x}}$  multiplicando ${\displaystyle V}$  pol cosα (siendo α l'ángulu formáu por ${\displaystyle V_{x}}$  y ${\displaystyle V}$ ) o multiplicando ${\displaystyle V}$  pol senβ (siendo β l'ángulu formáu por ${\displaystyle V_{y}}$  y ${\displaystyle V}$ ). D'igual forma puede calculase ${\displaystyle V_{y}}$  multiplicando ${\displaystyle V}$  pol senα o multiplicando ${\displaystyle V}$  pol cosβ (considerando les posiciones de α y β mentaes enantes).

Siendo'l vector la suma vectorial de les sos coordenaes:

${\displaystyle {\vec {V}}={\vec {V_{x}}}+{\vec {V_{y}}}}$ 

 

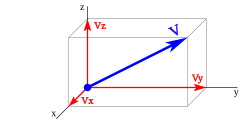
Si un vector ye de tres dimensiones reales, representáu sobre les exes x, y, z, puede representase:

${\displaystyle {\vec {V}}={\boldsymbol {V}}=(V_{x},V_{y},V_{z})}$ 

siendo les sos coordenaes:

${\displaystyle V_{x},\;V_{y},\;V_{z}}$ 

Si representamos el vector gráficamente podemos estremar los siguientes elementos:

La recta soporte o direición, sobre la que se traza'l vector.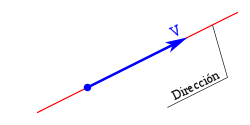  

El módulu o amplitú con un llargor proporcional al valor del vector.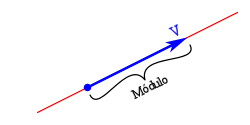  

El sentíu, indicáu pola punta de flecha, siendo unu de los dos posibles sobre la recta soporte.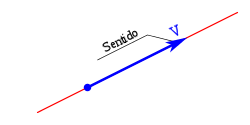  

El puntu d'aplicación que correspuende al llugar xeométricu al cual correspuende la carauterística vectorial representáu pol vector.  

El nome o denominación ye la lletra, signu o secuencia de signos que define al vector.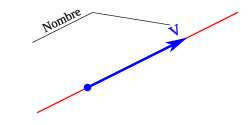  

Polo tanto nun vector podemos estremar:  

Nome :

Direición

Sentíu :

Módulu : Puntu d'aplicación

Magnitúes vectoriales

 

 

Frente a aquelles magnitúes físiques, tales como la masa, la presión, el volume, la enerxía, la temperatura, etc; que queden dafechu definíes por un númberu y les unidaes utilizaes na so midida, apaecen otres, tales como'l desplazamientu, la velocidá, l'aceleración, la fuercia, el campu llétrico, etc., que nun queden dafechu definíes dando un datu numbéricu, sinón que lleven acomuñaes una direición. Estes últimes magnitúes son llamaes vectoriales en contraposición a les primeres llamaes angulares.

Les magnitúes vectoriales queden representaes por un ente matemáticu que recibe'l nome de vector. Nun espaciu euclidianu, de non más de tres dimensiones, un vector representar por un segmentu empobináu. Asina, un vector queda carauterizáu polos siguiente elementos: el so llargor o módulu, siempres positivu por definición, y el so direición, que puede ser representada por aciu la suma de les sos #Componentes d'un vector componentes vectoriales ortogonales, paraleles a les exes de coordenaes; o por aciu coordenaes polares, que determinen l'ángulu que forma'l vector coles exes positives de coordenaes.

Represéntase como un segmentu empobináu, con una direición, dibuxáu de forma similar a una "flecha". El so llargor representa'l módulu del vector, la recta indica la direición, y la "punta de flecha" indica'l so sentíu.

Notación

Les magnitúes vectoriales representar nos testos impresos por lletres en negrina, pa estremales de les magnitúes angulares que se representen en cursiva. Nos testos manuscritos, les magnitúes vectoriales represéntense asitiando una flecha sobre la lletra que designa'l so módulu (el cual ye un angular).

Exemplos

• ${\displaystyle \mathbf {A} ,\ \mathbf {a} ,\ {\boldsymbol {\omega }},}$  ... representen, respeutivamente, les magnitúes vectoriales de módulos A, a, ω, ... El módulu d'una magnitú vectorial tamién se representa zarrando ente barres la notación correspondiente al vector: ${\displaystyle |\mathbf {A} |,\ |\mathbf {a} |,\ |{\boldsymbol {\omega }}|,}$  ...
• Nos testos manuscritos escríbese: ${\displaystyle {\vec {A}},\ {\vec {a}},\ {\vec {\omega }},}$ ... pa los vectores y ${\displaystyle |{\vec {A}}|,\ |{\vec {a}}|,\ |{\vec {\omega }}|,}$ ... o ${\displaystyle A,\ a,\ {\omega },}$ ... pa los módulos.

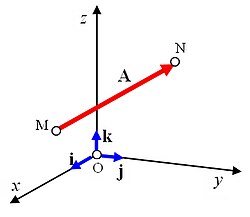
Cuando convenga, represéntense la magnitú vectorial faciendo referencia al orixe y al estremu del segmentu empobináu que lu representa geométricamente; asina, desígnense los vectores representaos na Figura 2 na forma ${\displaystyle \mathbf {A} ={\overrightarrow {MN}},\mathbf {B} ={\overrightarrow {OP}}\,}$ , ... resultando bien útil esta notación pa los vectores que representen el desplazamientu.

Amás d'estes convenciones los vectores unitarios o versores, que'l so módulu ye la unidá, represéntense frecuentemente con un circunflexu enriba, por casu ${\displaystyle \mathbf {\hat {o}} ,\mathbf {\hat {v}} }$ .

Clasificación de vectores

Según los criterios que s'utilicen pa determinar la igualdá o equipolencia de dos vectores, pueden estremase distintos tipos de los mesmos:

• Vectores llibres: nun tán aplicaos en nengún puntu en particular.
• Vectores esnidiosos: el so puntu d'aplicación puede esmucir a lo llargo de la so recta d'aición.
• Vectores fixos o amestaos: tán aplicaos nun puntu en particular.

Podemos referinos tamién a:

• Vectores unitarios: vectores de módulu unidá.
• Vectores concurrentes o angulares: son aquelles que les sos direiciones o llinies d'aición pasen por un mesmu puntu. Tamién se-yos suel llamar angulares porque formen un ángulu ente elles.
• Vectores opuestos: vectores d'igual magnitú y direición, pero sentíos contrarios. N'inglés dizse que son d'igual magnitú pero direiciones contraries, una y bones la direición tamién indica'l sentíu.
• Vectores colineales: los vectores que comparten una mesma recta d'aición.
• Vectores paralelos: si sobre un cuerpu ríxidu actúen dos o más fuercies que les sos llinies d'aición son paraleles.
• Vectores coplanarios: los vectores que les sos rectes d'aición son coplanarias (asitiaes nun mesmu planu).

Componentes d'un vector

 

Un vector nel espaciu euclideu tridimensional puede espresase como una combinación llinial de trés vectores unitarios o versores, que son perpendiculares ente sigo y constitúin una base vectorial.

En coordenaes cartesianes, los vectores unitarios representar por ${\displaystyle \mathbf {i} \,}$ , ${\displaystyle \mathbf {j} }$ , ${\displaystyle \mathbf {k} }$ , paralelos a les exes de coordenaes ${\displaystyle x}$ , ${\displaystyle y}$ , ${\displaystyle z}$  positivos. Les componentes del vector nuna base vectorial predeterminada pueden escribise ente paréntesis y separaes con comes:

${\displaystyle \mathbf {a} =(a_{x},a_{y},a_{z})}$ 

o espresase como una combinación de los vectores unitarios definíos na base vectorial. Asina, nun sistema de coordenaes cartesianu, va ser

${\displaystyle \mathbf {a} =a_{x}\,\mathbf {i} +a_{y}\,\mathbf {j} +a_{z}\,\mathbf {k} }$ 

Estes representaciones son equivalentes ente sigo, y los valores ${\displaystyle a_{x}}$ , ${\displaystyle a_{y}}$ , ${\displaystyle a_{z}}$ , son les componentes d'un vector que, sacantes s'indique lo contrario, son númberos reales.

Una representación conveniente de les magnitúes vectoriales ye por aciu un vector columna o un vector fila, particularmente cuando tán implicaes operaciones matrices (tales como'l cambéu de base), de la manera siguiente:

${\displaystyle \mathbf {a} ={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\\\end{bmatrix}}\qquad \mathbf {a} =[a_{x}\ a_{y}\ a_{z}]}$ 

Con esta notación, los vectores cartesianos queden espresaos de la siguiente manera:

${\displaystyle {\mathbf {i} }=[1\ 0\ 0],\ {\mathbf {j} }=[0\ 1\ 0],\ {\mathbf {k} }=[0\ 0\ 1]}$ 

El lema de Zorn, consecuencia del axoma d'elección, dexa establecer que tou espaciu vectorial almite una base vectorial, polo que tou vector ye representable como'l productu d'unes componentes al respeutive de dicha base. Dau un vector solo esisten un númberu finito de componentes distintos de cero.

Representación gráfica de los vectores

Hai persones que nun encamienta usar gráficos pa evitar el tracamundiu de conceutos y l'inducción al error, ensin investigación que la acote, tamién ye ciertu que la memoria aguiyar con meyores resultaos. Pa ello:

• Llámase vector a la representación visual col símbolu de flecha (un segmentu y un triángulu nun estremu).
• La derechura visual d'una flecha o combadura de la mesma, nun la fai distinta en símbolu si los dos estremos permanecen nel mesmu llugar y orde.
• El qu'una flecha cierre en sí mesma, indica l'ausencia d'efectos alxebraicos.
• Pa visualizar la suma de vectores va faese encadenándolos, esto ye, xuniendo l'estremu que tien un triángulu (final) del primer vector col estremu que nun lo tien (orixe) del segundu vector calteniendo la direición y distancia, mesmes al espaciu, de los sos dos estremos, una y bones estos dos cualidaes estremar visualmente d'otros vectores.
• Los angulares van representar con una llinia de trazos a manera, puramente, de distinción yá que non siempres pertenecen al espaciu de vectores.

Esamínense cada unu de los casos qu'apaecen na definición de les operaciones suma de vectores y productu por un angular:

Suma de vectores

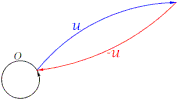
La definición suma de vectores nel orde o+v produz otru vector, ye como encadenar, siempres visualmente, un vector o y depués unu v. Vamos Dicir que o+v simplificar como un vector w o que w descompon como suma de vectores o y v.

 

1) Dicir que o+v=v+o, ye esixir que los dos sumas simplifiquen nel mesmu vector, en negru. Vease qu'en física los vectores en colloráu asemeyen la descomposición de fuercies exercíes pol vector negru nel so orixe, y represéntase con un paralelogramu.

 

2) Dicir que o+(v+w)=(o+v)+w, ye esixir que les simplificaciones de sumes de vectores puedan ser optatives en cualquier cadena de sumes.

 

3) Dicir qu'esiste un vector cero (elementu neutru) tal que o+0=o, equival a esixir qu'esista un vector incapaz d'efectuar, por aciu la suma, cambéu dalgunu a tolos vectores.

 

4) Dicir que o+(-o)=0, ye esixir la esistencia d'un elementu opuestu, -o, que sumáu a o simplifique nun vector cero.

 

Productu por un angular

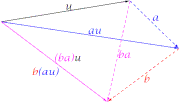
La definición productu por un angular ${\displaystyle a\cdot o}$  produz otru vector; ye como modificar l'estremu final del vector o, siempres visualmente.

Per un sitiu la representación del productu nel casu que'l cuerpu d'angular sía ${\displaystyle K=\mathbb {R} }$  modifica, visualmente, el llargor de la imaxe del vector, quedando dambos siempres superpuestos; per otru llau les representaciones nel casu que ${\displaystyle K=\mathbb {C} }$  amás de modificar el llargor, tamién amiesta rotaciones, pa facilitales visualmente considérense centraes nel orixe del vector, siendo estos cambeos un pocu más espresives, visualmente, pero non más fáciles que nel casu real:

 

a)Dicir que a(bu)=(ab)o, ye esixir que los productos encadenaos a(b(o)) pueden simplificase como unu, c=ab, depués (ab)o queda como cu.

 

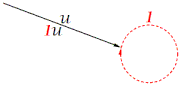
b) Dicir qu'esiste l'angular 1 tal que 1o=o, equival a dicir esista un angular incapaz d'efectuar, por aciu productu, cambéu dalgunu a tolos vectores.

 

c) Dicir que a(o+v)=au+av, ye esixir la propiedá distributiva respeuto la suma vectorial.

 

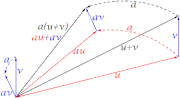
d) Dicir que (a+b)o=au+bu, ye esixir la propiedá distributiva respeuto la suma angular.

 

Pal casu real haber d'esaniciar les rotaciones de los exemplos anteriores.

Suma de vectores

Pa sumar dos vectores llibres (vector y vector) escuéyense como representantes dos vectores tales que l'estremu final d'unu coincida col estremu orixe del otru vector.

Suma de vectores sobre un mesmu puntu

La suma de vectores ta bien definida si ambos vectores pertenecen al mesmu espaciu vectorial, en física por que dos vectores puedan ser sumaos tienen de tar aplicaos nel mesmu puntu. La composición de fuercies sobre un sólidu ríxidu cuando los puntos d'aplicación nun coinciden lleva a la noción de momentu de fuercia daos dos fuercies ${\displaystyle \scriptstyle \mathbf {F} _{1},\mathbf {F} _{2}}$  con puntos d'aplicación ${\displaystyle \scriptstyle \mathrm {P} _{1},\mathrm {P} _{2}}$  defínense la fuercia resultante como'l par:^{[ensin referencies]}

${\displaystyle (\mathrm {P} _{R},\mathbf {F} _{R})=(\mathrm {P} _{1},\mathbf {F} _{1})\boxplus (\mathrm {P} _{2},\mathbf {F} _{2})}$ 

Onde ${\displaystyle \boxplus }$  ye la suma xeneralizada a vectores aplicaos en distintos puntos. El puntu d'aplicación ${\displaystyle \scriptstyle \mathrm {P} _{R}}$  ye'l puntu d'interseición de les rectes d'aición de les fuercies. Les componentes del vector de fuercia resultante ye de fechu la suma de componentes ordinaries de vectores:

${\displaystyle (\mathrm {P} _{R},\mathbf {F} _{R})=(\mathrm {P} _{R},\mathbf {F} _{1}+\mathbf {F} _{2})}$ 

El momentu resultante ye'l momentu de fuercia del conxuntu de fuercies respeuto al puntu calculáu pa la fuercia resultante.

Métodu del paralelogramu

 

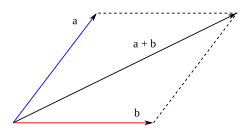
Esti métodu dexa solamente sumar vectores de dos en dos. Consiste en disponer gráficamente los dos vectores de manera que los oríxenes de dambos coincidan nun puntu, trazando rectes paraleles a cada unu de los vectores, nel estremu del otru y d'igual llargor, formando asina un paralelogramu (ver gráficu). El vector resultáu de la suma ye la diagonal de dichu paralelogramu que parte del orixe común de dambos vectores.

Métodu del triángulu o métodu poligonal

 

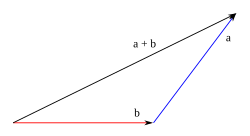
Consiste en disponer gráficamente un vector de siguío d'otru, ordenadamente: l'orixe de cada unu de los vectores va coincidir col estremu del siguiente. El vector resultante ye aquel que'l so orixe coincide col del primer vector y termina nel estremu del postreru.

==== Métodu analíticu pa la suma y diferencia de vectores Daos dos vectores llibres,

${\displaystyle \mathbf {a} =(a_{x}\mathbf {i} +a_{y}\mathbf {j} +a_{z}\mathbf {k} )}$ 

${\displaystyle \mathbf {b} =(b_{x}\mathbf {i} +b_{y}\mathbf {j} +b_{z}\mathbf {k} )}$ 

La resultancia de la so suma o de la so diferencia espresar en formar

${\displaystyle \mathbf {a} \pm \mathbf {b} =(a_{x}\mathbf {i} +a_{y}\mathbf {j} +a_{z}\mathbf {k} )\pm (b_{x}\mathbf {i} +b_{y}\mathbf {j} +b_{z}\mathbf {k} )}$ 

y ordenando les componentes,

${\displaystyle \mathbf {a} \pm \mathbf {b} =(a_{x}\pm b_{x})\mathbf {i} +(a_{y}\pm b_{y})\mathbf {j} +(a_{z}\pm b_{z})\mathbf {k} }$ 

Cola notación matricial sería

${\displaystyle \mathbf {a} \pm \mathbf {b} ={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\\\end{bmatrix}}\pm {\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\\\end{bmatrix}}={\begin{bmatrix}a_{x}\pm b_{x}\\a_{y}\pm b_{y}\\a_{z}\pm bz\\\end{bmatrix}}}$ 

Conocíos los módulos de dos vectores daos, ${\displaystyle \mathbf {a} }$  y ${\displaystyle \mathbf {b} }$ , según l'ángulu ${\displaystyle \theta }$  que formen ente sigo, el módulu de ${\displaystyle \mathbf {a} \pm \mathbf {b} }$  ye:

${\displaystyle |\mathbf {a} \pm \mathbf {b} |={\sqrt {a^{2}+b^{2}\pm 2ab\cos \theta }}\leq {\sqrt {a^{2}+b^{2}+2ab\cos \theta }}}$ 

La deducción d'esta espresión puede consultase en deducción del módulu de la suma.

Productu d'un vector por un angular

 

El productu d'un vector por un angular ye otru vector que'l so módulu ye'l productu del angular pol módulu del vector, que la so direición ye igual a la del vector, y que'l so sentíu ye contrariu a esti si l'angular ye negativu.

Partiendo de la representación gráfica del vector, sobre la mesma llinia de la so direición tomamos tantes vegaes el módulu de vector como indica l'angular.

Sían ${\displaystyle p\,}$  un angular y ${\displaystyle \mathbf {a} }$  un vector, el productu de ${\displaystyle p\,}$  por ${\displaystyle \mathbf {a} }$  represéntase ${\displaystyle p\,\mathbf {a} }$  y realízase multiplicando caúna de les componentes del vector pol angular; esto ye,

${\displaystyle p\,\mathbf {a} =pa_{x}\mathbf {i} +pa_{y}\mathbf {j} +pa_{z}\mathbf {k} }$ 

Cola notación matricial sería

${\displaystyle p\,\mathbf {a} =p\,{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\\\end{bmatrix}}={\begin{bmatrix}p\,a_{x}\\p\,a_{y}\\p\,a_{z}\\\end{bmatrix}}}$ 

Productu angular

Productu vectorial

=== Derivada ordinaria d'un vector Dau un vector que ye función d'una variable independiente

${\displaystyle \mathbf {a} (t)=a_{x}(t)\mathbf {i} +a_{y}(t)\mathbf {j} +a_{z}(t)\mathbf {k} }$ 

Calculamos la derivada ordinaria del vector con respectu de la variable t, calculando la derivada de caúna de los sos componentes como si d'angulares tratárase:

${\displaystyle {\frac {d}{dt}}\mathbf {a} (t)={\frac {d}{dt}}a_{x}(t)\mathbf {i} +{\frac {d}{dt}}a_{y}(t)\mathbf {j} +{\frac {d}{dt}}a_{z}(t)\mathbf {k} }$ 

teniendo en cuenta que los vectores unitarios son constantes en módulu y direición.

Con notación matricial sería

${\displaystyle {\frac {d}{dt}}\mathbf {a} (t)={\frac {d}{dt}}\,{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\\\end{bmatrix}}={\begin{bmatrix}{\frac {d}{dt}}a_{x}\\{\frac {d}{dt}}a_{y}\\{\frac {d}{dt}}a_{z}\\\end{bmatrix}}}$ 

 

Veamos un exemplu de derivación d'un vector, partiendo d'una función vectorial:

${\displaystyle \mathbf {r} (t)=\sin(t)\mathbf {i} +\cos(t)\mathbf {j} +5t\mathbf {k} }$ 

Esta función representa una curva helicoidal alredor de la exa z, de radio unidá, como s'ilustra na figura. Podemos imaxinar qu'esta curva ye la trayeutoria d'una partícula y la función ${\displaystyle \mathbf {r} (t)\,}$  representa'l vector posición en función del tiempu t. Derivando vamos tener:

${\displaystyle {\frac {d\mathbf {r} (t)}{dt}}={\frac {d}{dt}}\sin(t)\mathbf {i} +{\frac {d}{dt}}\cos(t)\mathbf {j} +{\frac {d}{dt}}5t\mathbf {k} }$ 

Realizando la derivada:

${\displaystyle {\frac {d\mathbf {r} (t)}{dt}}=\cos(t)\mathbf {i} -\sin(t)\mathbf {j} +5\mathbf {k} }$ 

La derivada del vector posición respectu al tiempu ye la velocidá, asina que esta segunda función determina'l vector velocidá de la partícula en función del tiempu, podemos escribir:

${\displaystyle \mathbf {v} (t)=\cos(t)\mathbf {i} -\sin(t)\mathbf {j} +5\mathbf {k} }$ 

Esti vector velocidá ye un vector tanxente a la trayeutoria nel puntu ocupáu pola partícula en cada intre. El sentíu ye escontra los valores crecientes de los valores angulares. Si deriváramos de nuevu llograríamos el vector aceleración.

Derivada covariante d'un vector

Cuando en llugar d'emplegar una "base fixa" en tol dominiu d'un vector úsense "bases móviles" como cuando s'empleguen coordenaes curvillinies la variación total d'un vector dependiente del tiempu depende non solo de la variación de componentes como nel casu de la derivada ordinaria sinón tamién de la variación de la orientación de la base. La variación total llámase derivada covariante:

${\displaystyle {\frac {\delta }{\delta t}}\mathbf {a} (t)=\sum _{k}\left({\dot {a}}^{k}\mathbf {y} _{k}+a^{k}{\dot {\mathbf {y} }}_{k}\right)={\frac {d}{dt}}\mathbf {a} (t)+\mathbf {a} (t)\times {\boldsymbol {\omega }}(t)}$ 

Cuando s'emplega una base fixa (coordenaes cartesianes) la derivada covariante coincide cola derivada ordinaria. Por casu cuando s'estudia'l movimientu d'una partícula dende un sistema de referencia non inercial en rotación, les aceleraciones de Coriolis y centrípeta deber a los factores que contienen ${\displaystyle {\boldsymbol {\omega }}}$  y otros factores menos comunes.

Ángulu ente dos vectores

L'ángulu determináu poles direiciones de dos vectores ${\displaystyle \mathbf {a} }$  y ${\displaystyle \mathbf {b} }$  vien dau por:

${\displaystyle \cos \theta ={\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} |\,|\mathbf {b} |}}}$ 

=== Descomposiciones d'un vector Dau un vector ${\displaystyle \mathbf {a} }$  y una direición de referencia dada por un vector unitariu ${\displaystyle \mathbf {n} }$  puede descomponese el primer vector nuna componente paralela y otra componente perpendicular a la direición de referencia:

${\displaystyle \mathbf {a} =\mathbf {a} _{\|}+\mathbf {a} _{\bot }=(\mathbf {n} \cdot \mathbf {a} )\mathbf {n} +(\mathbf {n} \times \mathbf {a} )\times \mathbf {n} }$ 

En física esta descomposición usar en distintos contestos como descomponer l'aceleración nuna componente paralela a la velocidá y otra componente perpendicular a la mesma. Tamién el tensión mecánico nun puntu sobre un planu puede descomponese nuna componente normal al planu y otra paralela.

Tamién dau un campu vectorial ${\displaystyle \mathbf {o} (\mathbf {x} )}$  definíu sobre un dominiu de Lipschitz, acutáu, a cencielles conexu y de cuadráu integrable ${\displaystyle \mathbf {o} \in (L^{2}(\Omega ))^{3}}$  almite la llamada descomposición de Helmholtz como suma d'un campu conservativo y un campu solenoidal:

${\displaystyle \mathbf {o} =\mathbf {o} _{C}+\mathbf {o} _{S}=({\boldsymbol {\nabla }}\varphi )+({\boldsymbol {\nabla }}\times \mathbf {A} )}$ 

 

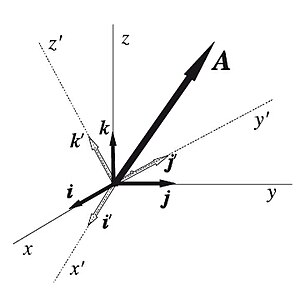
En matemátiques les rotaciones son tresformamientos lliniales que caltienen les normes n'espacios vectoriales nos que se definió una operación de productu interior. La matriz de tresformamientu tien la propiedá de ser una matriz unitaria, esto ye, ye ortogonal y la so determinante ye 1. Sía un vector ${\displaystyle \scriptstyle \mathbf {A} }$  espresáu nun sistema de coordenaes cartesianes (x, y, z) con una base vectorial ${\displaystyle {\mathcal {B}}}$  asociada definida polos versores ${\displaystyle \left(\mathbf {i} ,\mathbf {j} ,\mathbf {k} \,\right)}$ ; esto ye,

${\displaystyle \mathbf {A} ={\begin{bmatrix}A_{x}\\A_{y}\\A_{z}\end{bmatrix}}_{\mathcal {B}}}$ 

Agora, supongamos que xiramos el sistema d'exes coordenaes, calteniendo fixu l'orixe del mesmu, de cuenta que llogremos un nuevu triedru ortogonal d'exes (x′, y′, z′), con una base vectorial ${\displaystyle {\mathcal {B}}'}$  asociada definida polos versores ${\displaystyle \left(\mathbf {i} ',\mathbf {j} ',\mathbf {k} '\,\right)}$ . Les componentes del vector ${\displaystyle \mathbf {A} \,}$  nesta nueva base vectorial van ser:

${\displaystyle \mathbf {A} ={\begin{bmatrix}A'_{x}\\A'_{y}\\A'_{z}\end{bmatrix}}_{{\mathcal {B}}'}}$ 

La operación de rotación de la base vectorial siempres puede espresase como l'aición d'un operador llinial (representáu por una matriz) actuando sobre'l vector (multiplicando al vector):

${\displaystyle \mathbb {R} \,\mathbf {A} _{\mathcal {B}}=\mathbf {A} _{{\mathcal {B}}'}}$ 

que ye la matriz de tresformamientu pal cambéu de base vectorial.

 

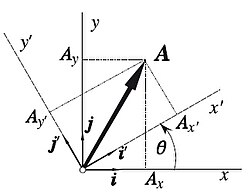
Exemplu

Nel casu simple nel que'l xiru tenga magnitú ${\displaystyle \theta \,}$  alredor de la exa z, vamos tener el tresformamientu:

${\displaystyle \mathbb {R} ={\begin{bmatrix}\cos \theta &\sin \theta &0\\-\sin \theta &\cos \theta &0\\0&0&1\\\end{bmatrix}}}$ 

Al faer l'aplicación del operador, esto ye, al multiplicar la matriz pol vector, vamos llograr la espresión del vector ${\displaystyle \mathbf {A} \,}$  na nueva base vectorial:

${\displaystyle {\begin{bmatrix}\cos \theta &\sin \theta &0\\-\sin \theta &\cos \theta &0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}A_{x}\\A_{y}\\A_{z}\end{bmatrix}}_{\mathcal {B}}={\begin{bmatrix}A'_{x}\\A'_{y}\\A'_{z}\end{bmatrix}}_{{\mathcal {B}}'}}$ 

siendo

${\displaystyle A'_{x}=A_{x}\cos \theta +A_{y}\sin \theta \,}$ 
${\displaystyle A'_{y}=-A_{x}\sin \theta +A_{y}\cos \theta \,}$ 
${\displaystyle A'_{z}=A_{z}\,}$ 

les componentes del vector na nueva base vectorial.

Non cualesquier n-tupla de funciones o númberos reales constitúi un vector físicu. Por que una n-tupla represente un vector físicu, los valores numbéricos de les componentes del mesmu midíos por distintos observadores tienen de tresformase acordies con ciertes rellaciones fixes.

En mecánica newtoniana xeneralmente utilícense vectores xenuinos, llamaos dacuando vectores polares, xunto con pseudovectores, llamaos vectores axiales que realmente representen el dual de Hodge de magnitúes tensoriales antisimétricas. El momentu angular, el campu magnéticu y toles magnitúes en que la so definición intervién el productu vectorial son en realidá pseudovectores o vectores axiales.

En teoría especial de la relatividá, solo los vectores tetradimensionales que les sos midíes tomaes por distintos observadores pueden ser rellacionaes por aciu dalguna tresformamientu de Lorentz constitúin magnitúes vectoriales. Asina les componentes de dos magnitud vectoriales midíes por dos observadores ${\displaystyle O\,}$  y ${\displaystyle O'}$  tienen de rellacionase acordies cola siguiente rellación:

${\displaystyle {V'}^{\beta }=\sum _{\alpha =0}^{3}\Lambda _{\alpha }^{\beta }\ V^{\alpha }}$ 

Onde ${\displaystyle \Lambda _{\alpha }^{\beta }}$  son les componentes de la matriz que da'l tresformamientu de Lorentz. Magnitúes como'l momentu angular, el campu llétrico o'l campu magnéticu de fechu en teoría de la relatividá nun son magnitúes vectoriales sinón tensoriales.

• Ortega, Manuel R. (1989-2006). leición de Física (4 volumes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
• Resnick, Robert & Krane, Kenneth S. (2001). Physics (n'inglés). New York: John Wiley & Sons.
• Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6ª (n'inglés), Brooks/Cole. ISBN 0-534-40842-7.
• Tipler, Paul A. (2000). Física pa la ciencia y la teunoloxía (2 volumes). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.

• Weisstein, Eric W. «Vector» (inglés). MathWorld. Wolfram Research.