رياضيات زمرة

المثال الأول: الأعداد الصحيحة

من أشهر الأمثلة على الزمر مجموعة الأعداد الصحيحة Z، وهي تتكون من الأعداد التالية:

..., 4, 3, 2, 1, 0, 1-, 2-, 3-, 4- , ... مزودةً بعملية الجمع.

الخصائص التالية لعملية جمع الأعداد الصحيحة نموذجٌ للبديهيات التجريدية للزمر.

1. مجموع عددين صحيحين هو عدد صحيح. ولا يمكن نهائيا أن يكون مجموع عددين صحيحين عددًا غير صحيح. تعرف هذه الخاصية باسم الانغلاق بالنسبة للجمع.
2. بالنسبة لثلاثة أعداد a و b و c، فإن (a + b) + c = a + (b + c). أي أنه إذا جُمعت a و b أولًا، ثم أُضيفت c، فسيُحصل على نفس النتيجة إذا ما جمعت a مع حاصل مجموع b و c. تعرف هذه الخاصية باسم التجميعية.
3. إذا كان a عددًا صحيحًا، فإن a + 0 = 0 + a = a. الصفر يسمى عنصرا محايدا.
4. لكل عدد صحيح a، يوجد عدد صحيح b حيث a + b = b + a = 0. العدد الصحيح b يسمى العنصر المعاكس للعدد a ويُكتب a-.

تشكل زمرة الأعداد الصحيحة تحت عملية الجمع كائنًا رياضيًّا ينتمي إلى تصنيف واسع من الكائنات الأخرى تشاركه خصائصه البنيوية. وقد طُور التعريف التجريدي التالي لفهم هذه البنى فهمًا شاملًا.

تعريف

الزمرة هي مجموعة ${\displaystyle G\!}$  مزودة بعملية ثنائية يرمز لها بالرمز ${\displaystyle \bullet }$  وتسمى قانون الزمرة لـ ${\displaystyle G\!}$  أو عملية الزمرة، تربط كل عنصرين اثنين ${\displaystyle a}$  و ${\displaystyle b}$  من عناصرها بعنصر ثالث ${\displaystyle c}$  ينتمي إلى نفس الزمرة. توجد عدة طرق للتعبير عن عملية الزمرة كتابةً، منها ${\displaystyle c=a\bullet b}$  أو ${\displaystyle c=ab}$ ، وفي الزمر الأبيلية غالبًا ما تُكتب ${\displaystyle c=a+b}$ ، وتُستخدم طرق أخرى للتعبير عن عمليات الزمر مثل ${\displaystyle c=a\circ b}$  أو ${\displaystyle c=a*b}$ . وكل من المجموعة والعملية ${\displaystyle (G,\bullet )}$  يحققان البديهيات التالية:

الانغلاق

لكل عنصرين ${\displaystyle a}$  و ${\displaystyle b}$  من عناصر ${\displaystyle G\!}$  يكون ناتج العملية ${\displaystyle a\bullet b}$  منتميًا أيضًا إلى ${\displaystyle G\!}$ .^3[›]

التجميعية

لكل ثلاثة عناصر ${\displaystyle a}$  و ${\displaystyle b}$  و ${\displaystyle c}$  من ${\displaystyle G\!}$  يكون ${\displaystyle (a\bullet b)\bullet c=a\bullet (b\bullet c)}$ ، أي أن ناتج تركيب العناصر الثلاثة لا يتأثر بتغير موضع الأقواس،^4[›] مما يسمح بكتابة الناتج في صورة ${\displaystyle a\bullet b\bullet c}$  بدون أقواس.

وجود العنصر المحايد

يوجد عنصر ${\displaystyle e\in G\!}$  يحقق المعادلة ${\displaystyle e\bullet a=a\bullet e=a}$  لكل ${\displaystyle a\in g}$ ، ويسمى هذا العنصر العنصر المحايد. وهو عنصر وحيد؛ فلا يوجد أكثر من عنصر محايد واحد في الزمرة.^5[›]

وجود العنصر المعاكس

لكل عنصر ${\displaystyle a}$  من عناصر ${\displaystyle G\!}$  يوجد عنصر ${\displaystyle b}$  من ${\displaystyle G\!}$  بحيث ${\displaystyle a\bullet b=b\bullet a=e}$  حيث ${\displaystyle e}$  هو العنصر المحايد، أي أن تركيب هذين العنصرين بأي ترتيب يساوي العنصر المحايد ${\displaystyle e}$ . يُسمي العنصر ${\displaystyle b}$  العنصر المعاكس للعنصر ${\displaystyle a}$  ورمزه ${\displaystyle a^{-1}}$ . ومن الواضح أن العنصر المحايد واحد فقط في الزمرة، وأن العنصر المعاكس للعنصر ${\displaystyle a}$  محدد بوضوح.

هذا وقد يتغير ناتج العملية بتغير ترتيب أطرافها، وبعبارة أخرى فإن ناتج دمج العنصر ${\displaystyle a}$  مع العنصر ${\displaystyle b}$  ليس بالضرورة مساويًا لناتج دمج العنصر ${\displaystyle b}$  مع العنصر ${\displaystyle a}$ ، فهذه المعادلة:

${\displaystyle a\bullet b=b\bullet a}$ 

قد لا تكون صحيحة دائمًا. تتحقق هذه المعادلة دائمًا في زمرة الأعداد الصحيحة بالنسبة لعملية الجمع؛ وهذا لأن ${\displaystyle a+b=b+a}$  لأي عددين صحيحين (إبدالية الجمع). ويطلق على الزمر التي تحقق دومًا المعادلة ${\displaystyle a\bullet b=b\bullet a}$  الزمر الأبيلية (تخليدًا لنيلس أبيل). وتعد زمرة التماثل (التالي شرحها) مثالًا للزمر غير الأبيلية.

كثيرًا ما يُكتب العنصر المحايد ${\displaystyle 1}$  أو ${\displaystyle 1_{G}\!}$ ، وهذا الرمز مأخوذ من المحايد الضربي. كما قد يُكتب العنصر المحايد ${\displaystyle 0}$  خاصة إذا رُمز لعملية الزمرة بـ${\displaystyle +}$ ، وتسمى الزمرة في هذه الحالة زمرة جمعية. وقد يُكتب العنصر المحايد أيضًا ${\displaystyle id}$ .

المثال الثاني: زمرة التماثل

يتطابق الشكلان في نفس المستوى إذا أمكن أن يحوَّل أحدهما إلى الآخر باستخدام مزيج من الدورانات والانعكاسات والانزلاقات. يتطابق كل شكل بديهيًّا مع نفسه. ومع ذلك فإن بعض الأشكال تتطابق مع نفسها بعدة طرق. تسمى هذه التطابقات الإضافية التماثلات. للمربع ثمانية تماثلات، كما توضح تلك الصور:

id(بترك كل عنصر على حاله)	r1 (بالدوران 90° يمينًا)	r2 (بالدوران 180° يمينًا)	r3 (بالدوران 270° يمينًا)
fv (بالانعكاس عموديًّا)	fh (بالانعكاس أفقيًّا)	fd (بالانعكاس القطري)	fc (بالانعكاس القطري المعاكس)
عناصر زمرة التماثل للمربع (D4). لُونت ورُقمت رؤوس المربع فقط من أجل توضيح العملية.

• العملية المحايدة تحفظ الشكل من التغيير كما في الشكل id.
• دوران المربع حول مركزه بزوايا 90° يمينًا و 180° يمينًا و 270° يمينًا ينتج عنه الأشكال r₁ و r₂ و r₃ على الترتيب.
• الانعكاس عبر المحورين العمودي والأفقي يعطي الشكلين f_h و f_v، والانعكاس عبر القطرين يعطي f_d و f_c.

تنتج هذه التماثلات عن مجموعة من الدوال، يقوم كل منها بإرسال نقطة في المربع إلى النقطة المناظرة لها في إطار التماثل. على سبيل المثال، في الشكل r₁ ترسل الدالة كل نقطة إلى صورتها بالدوران 90° يمينًا حول مركز المربع، أما في الشكل f_h فترسل كل نقطة إلى انعكاسها عبر محور المربع العمودي، وتركيب اثنتين من دوال التماثل الموجودة في الأشكال أعلاه يعطي دالة تماثل أخرى. تشكل هذه التماثلات زمرة تسمى الزمرة الزوجية وهي من الدرجة 4 ورمزها D₄، ومجموعة تلك الزمرة هي تلك المجموعة من دوال التماثل، وعمليتها هي تركيب الدوال. يمكن تركيب اثنين من التماثلات من خلال تركيب دالتيهما، بمعنى تطبيق الدالة الأولي على المربع، ومن ثم تطبيق الدالة الثانية على نتيجة الدالة الأولى. تُكتب نتيجة تطبيق الدالة الأولى a ثم الدالة الثانية b رمزيًّا من اليمين إلى اليسار كالتالي:

${\displaystyle b\bullet a}$  (الترميز من اليمين إلى اليسار هو نفسه المتبع عند تركيب الدوال).

يعدد جدول الزمرة على اليسار نتائج جميع هذه التراكيب الممكنة. على سبيل المثال، بالدوران بزاوية 270° يمينًا (r₃) ثم قلب الناتج أفقيًّا (f_h) نحصل على نفس الناتج الذي نحصل عليه بالانعكاس القطري (f_d). بالاستعانة بالجدول نستنتج أن:

${\displaystyle f_{h}\bullet r_{3}=f_{d}}$ 

يمكن تطبيق بديهيات الزمر على الزمرة D₄ المعرفة عناصرها وعمليتها في الجدول وحيث ${\displaystyle a,b,c\in D\!_{4}}$  كالتالي:

1. تحقيق بديهية الانغلاق يتطلب أن يكُون ${\displaystyle b\bullet a\in D\!_{4}}$  أي أن يكون تماثلًا أيضًا. هذا مثال أخر على عملية الزمرة اعتمادًا على الجدول في اليسار:
   ${\displaystyle r_{3}\bullet f_{h}=f_{c}}$ 
   أي أن الدوران بزاوية 270° يمينًا بعد الانعكاس أفقيًّا يساوي الانعكاس القطري العكسي. والمغزى أن أي تركيب لتماثلين يكون تماثلًا آخر من نفس الدرجة، يُمكن التأكد من ذلك بالاستعانة بالجدول في اليسار.
2. تتعامل التجميعية مع العمليات التي يركَّب فيها أكثر من تماثلين. توجد طريقتان نستطيع بها استخدام العناصر a و b و c على الترتيب لتكوين تماثل لمربع: الأولى هي أن يركَّب العنصران a و b في تماثل واحد أولًا، ثم أن يركَّب هذا التماثل مع c. والطريقة الأخرى هي أن يركَّب أولًا b و c، ثم أن يركَّب التماثل الناتج مع a. في حالة التجميعية يكون:
   ${\displaystyle (a\bullet b)\bullet c=a\bullet (b\bullet c)}$ 
   وهذا يعني أن ناتجي هاتين الطريقتين متساويان، أي يمكن تبسيط ناتج تركيب العديد من العناصر في الزمرة بجعلها في شكل تجميعات. فمثلًا ${\displaystyle (f_{d}\bullet f_{v})\bullet r_{2}=f_{d}\bullet (f_{v}\bullet r_{2})}$ ، ويمكن التأكد من هذا باستخدام الجدول في اليسار، فيلاحَظ أن
   ${\displaystyle (f_{d}\bullet f_{v})\bullet r_{2}=r_{3}\bullet r_{2}=r_{1}}$ ، وهذا يساوي
   ${\displaystyle f_{d}\bullet (f_{v}\bullet r_{2})=f_{d}\bullet f_{h}=r_{1}}$ .
   ومع أن شرط التجميعية صحيح في حالتي تركيب تماثلات المربع وجمع الأعداد، فهو ليس صحيحًا لكل العمليات؛ فطرح الأعداد مثلُا ليس عملية تجميعية، فمثلًا (7 − 3) − 2 = 2، وهذا لا يساوي 7 − (3 − 2) = 6.
3. العنصر المحايد في الزمرة المعطاة أعلاه هو التماثل id لتركه نقاط الشكل دون تغيير: تأدية id بعد a (أو a بعد id) يساوي التماثل a، وبتعبير رمزي:
   ${\displaystyle id\bullet a=a\bullet id=a}$ .
4. بالنسبة للزمرة المعطاة يقوم العنصر المعاكس بإبطال تحويلات بعض العناصر الأخرى. كل تماثل في الزمرة المعطاة يمكن إبطاله؛ فكل من التماثل المحايد id والانعكاسات f_h و f_v و f_d و f_c والدوران بزاوية 180° (r2)—كل منهم معكوس لذاته، لأن تأدية أحدهم مرتين يُعيد المربع إلى أصله قبل تأديته. بالإضافة إلى أن كلا الدورانين r₃ و r₁ معكوس للآخر، لأن الدوران 90° ثم إتباعه بدوران 270° (أو العكس بالعكس) يعطي دورانًا بزاوية 360°وينتهي بعدم حدوث تغير في المربع. وبالتعبير الرمزي:
   ${\displaystyle f_{h}\bullet f_{h}=r_{3}\bullet r_{1}=r_{1}\bullet r_{3}=id}$ .

وعلى عكس زمرة الأعداد الصحيحة التي ذُكر عنها في الأعلى أن ترتيب العملية لا يؤثر في الناتج، نجد الناتج يختلف في حالة الزمرة D₄، فمثلًا: ${\displaystyle f_{h}\bullet r_{1}=f_{c}}$  لكن ${\displaystyle r_{1}\bullet f_{h}=f_{d}}$ . ولذلك فإن الزمرة D₄ غير أبيلية.

تطور المفهوم العصري للزمرة المجردة انطلاقًا من مجموعة من مجالات الرياضيات؛ فقد كان أول حافز نحو نظرية الزمر هو محاولة حلحلة المعادلات الحدودية من الدرجة الخامسة فما فوق. طور عالم الرياضيات الفرنسي إيفاريست غالوا في القرن التاسع عشر أعمال كل من باولو روفيني وجوزيف لاغرانج، ليعطي معيارًا لقابلية حلحلة معادلة حدودية ما، بالنظر إلى زمرة التماثل المكونة من جذور هاته الحدودية. تتطابق عناصر هاته الزمرة والمسماة زمرة غالوا، مع تباديل ما للجذور. رفض معاصرو غالوا أفكاره في بادئ الأمر، ولم تنشر إلا بعد وفاته. درس أوغستين لوي كوشي لاحقًا زمر التبديلات الأكثر تعميمًا بشكل تخصصي. عرَّف أرثور كايلي الزمر المنتهية تجريديًّا لأول مرة في كتابه حول نظرية الزمر، اعتمادًا على المعادلة الرمزية θⁿ = 1 (المنشور عام 1854).

كانت الهندسة الرياضية ثاني مجال يستعمل الزمر بشكل منهجي، وقد ظهر ذلك بشكل خاص في استعمال زمر التماثل جزءً من برنامج إرلنغن الذي نشره فيليكس كلاين عام 1872. مع ظهور الفروع الهندسية الحديثة كالهندسة الزائدية والهندسة الإسقاطية، استخدم كلاين نظرية الزمر في تنظيم تلك الفروع لتصبح أكثر تماسكًا. طور سوفوس لي جميع هاته الأفكار، مؤسسًا دراسة زمر لي عام 1884.

أما المجال الثالث الذي كان وراء تطور نظرية الزمر فهو نظرية الأعداد. استعمل كارل فريدريش غاوس بُنى بعض الزمر الأبيلية ضمنيًّا في عمل حول نظرية الأعداد، والذي يحمل عنوان استفسارات حسابية (عام 1798)، كما استعملها ليوبلد كرونكر بشكل أكثر وضوحًا. في عام 1847، كان إرنشت كومر من بين العلماء الأوائل الذين حاولوا حلحلة مبرهنة فيرما الأخيرة، وذلك بتطوير زمر تصف تحليل عدد صحيح إلى أعداد أولية.

وضع كامي جوردان أول نظرية موحدة للزمر بالمفاضلة بين تلك المصادر المتعددة في عمله Traité des substitutions et des équations algébriques الصادر عام 1870. أعطى فالتر فون ديك البيان الأول للتعريف الحديث للزمرة المجردة. مع بداية القرن العشرين، اكتسبت الزمر اهتمامًا كبيرًا من الرياضياتيين، فظهرت أعمال فرديناند جورج فروبنيوس وويليام برنسايد الرائدة في نظرية التمثيل للزمر المنتهية، وكذلك أعمال ريتشارد براور في نظرية التمثيل النمطي، وأوراق إيساي شور. درس هيرمان فايل وإيلي كارتن وغيرهما الكثير نظرية زمر لي خاصةً والزمر محلية التراص عامةً. صيغت نظرية الزمر الجبرية لأول مرة على يد كلود شيفالي في أواخر ثلاثينيات القرن العشرين وعلى يد أرمان بورل وجاك تيتس لاحقًا.

نظمت جامعة شيكاغو في 1960–61 عامًا خاصًّا لنظرية الزمر، وقد استقطب هذا الحدث علماء نظرية الزمر مثل دانيال غورنشتاين وجون تومسون وفالتر فايت، وبمساهمة العديد من الرياضياتيين الآخرين صُنفت كل الزمر المنتهية البسيطة عام 1982. تفوق هذا المشروع على نظائره السابقة بحجمه الهائل من ناحيتي طول البرهان وعدد الباحثين. ولا يزال البحث جاريًا لمحاولة تبسيط برهان التصنيف. ولا تزال نظرية الزمر حتى هذه الأيام فرعًا رياضيًّا نشطًا للغاية ومؤثرًا في عدة مجالات أخرى.^1[›]

عادة ما تندرج الحقائق الأساسية عن الزمر التي يمكن استنتاجها مباشرة من البديهيات تحت ما يُعرف بنظرية الزمر الابتدائية. فمثلًا تُظهر التطبيقات المتكررة لبديهية التجميعية أن القاعدة:

${\displaystyle a\bullet b\bullet c=(a\bullet b)\bullet c=a\bullet (b\bullet c)}$ 

تعمَّم لكل ما زاد على ثلاثة عوامل. وعادة ما تُحذف الأقواس في هذه الحالة لأنه يجوز وضعها في أي مكان داخل تلك السلسلة.

يمكن غض النظر جزئيًّا عن البديهيات، فنفترض وجود المحايد الأيسر والمعاكس الأيسر؛ إذ يمكن لكليهما أن يبدوا في الواقع ذوَي جهة، والنتيجة من ذلك ستكافئ التعريف المذكور أعلاه كالتالي.

وحدة العنصر المحايد ووحدة العناصر المعاكسة

إن وحدة العنصر المحايد والعناصر المعاكسة لكل عنصر نتيجتان مهمتان لبديهيات الزمر. ولا يمكن لزمرة ما أن تحتوي على أكثر من عنصر محايد واحد، وكل عنصر في الزمرة يملك عنصرًا مقابلًا واحدًا بالضبط. وبالتالي فمن الشائع تعريفهما بقول المحايد والمعاكس.

لإثبات وحدة العنصر المعاكس للعنصر ${\displaystyle a}$ ، لنفترض أن للعنصر ${\displaystyle a}$  عنصران معاكسان ${\displaystyle b}$  و ${\displaystyle c}$  في الزمرة ${\displaystyle (G\!,\bullet )}$ ، حيث

${\displaystyle b}$	${\displaystyle =}$	${\displaystyle b\bullet e}$		حيث ${\displaystyle e}$  هو العنصر المحايد
	${\displaystyle =}$	${\displaystyle b\bullet (a\bullet c)}$		لأن ${\displaystyle c}$  هو العنصر المعاكس للعنصر ${\displaystyle a}$ ، وبالتالي ${\displaystyle e=a\bullet c}$
	${\displaystyle =}$	${\displaystyle (b\bullet a)\bullet c}$		لأن خاصية التجميعية تقضي بحرية ترتيب الأقواس
	${\displaystyle =}$	${\displaystyle e\bullet c}$		لأن ${\displaystyle b}$  هو معاكس ${\displaystyle a}$ ، أي أن ${\displaystyle b\bullet a=e}$
	${\displaystyle =}$	${\displaystyle c}$		حيث ${\displaystyle e}$  هو العنصر المحايد

وبالتالي فإن كلا العنصرين ${\displaystyle b}$  و ${\displaystyle c}$  متساويان. وبعبارة أخرى فإن للعنصر ${\displaystyle a}$  معاكسًا واحدًا فقط. ويمكن إثبات وحدة العنصر المحايد في زمرة ما بنفس الطريقة، فلنفترض أن ${\displaystyle G\!}$  زمرة بها عنصران محايدان ${\displaystyle e}$  و ${\displaystyle f}$ ، حيث ${\displaystyle e=e\bullet f=f}$ ، وبالتالي فإن ${\displaystyle e}$  و ${\displaystyle f}$  متساويان.

القسمة

من الممكن القيام بعملية القسمة في الزمر: ليكن ${\displaystyle a}$  و ${\displaystyle b}$  عنصرين من الزمرة ${\displaystyle G\!}$ ، إذن هناك حل وحيد ${\displaystyle x}$  للمعادلة ${\displaystyle x\bullet a=b}$ . وبضرب حدي هاته المعادلة في العنصر ${\displaystyle a^{-1}}$  من الجهة اليمنى يعطي الحل ${\displaystyle x=x\bullet a\bullet a^{-1}=b\bullet a^{-1}}$ . ويوجد بالمثل حل وحيد ${\displaystyle y}$  في ${\displaystyle G\!}$  للمعادلة ${\displaystyle a\bullet y=b}$ ، وهو ${\displaystyle y=a^{-1}\bullet b}$ . وليس من الضروري عامةً لكل من ${\displaystyle x}$  و ${\displaystyle y}$  أن يتفقا.

إن نتيجة ذلك هي أن الضرب في العنصر ${\displaystyle g}$  من زمرة ما هو دالة تقابلية. وعلى وجه التحديد، إذا كان ${\displaystyle g}$  عنصرًا من الزمرة ${\displaystyle G\!}$  فإنه يوجد دالة تقابلية على ${\displaystyle G\!}$  تدعى الانزلاق الأيسر بـ ${\displaystyle g}$ ، وهو يرسل ${\displaystyle h\in G\!}$  إلى ${\displaystyle g\bullet h}$ . وبالمثل يوجد دالة تقابلية على ${\displaystyle G\!}$  تدعى الانزلاق الأيمن بـ ${\displaystyle g}$ ، وهو يرسل ${\displaystyle h}$  إلى ${\displaystyle h\bullet g}$ . وإذا كانت ${\displaystyle G\!}$  أبيلية فإن الانزلاقين الأيمن والأيسر بعنصر من عناصرها هما ذاتهما.

تُستخدم رموز رياضية في هذا القسم مثل ${\displaystyle X\!=\{x,y,z\}}$  للرمز إلى مجموعة X تحتوي العناصر x و y و z، أو يُستخدم بدلًا من ذلك ${\displaystyle x\in X\!}$  لتوضيح أن ${\displaystyle x}$  عنصر من ${\displaystyle X}$ . ويشير الترميز ${\displaystyle f\colon X\rightarrow Y}$  إلى أن ${\displaystyle f}$  هي دالة تربط بكل عنصر من ${\displaystyle X\!}$  عنصرًا من ${\displaystyle Y}$ .

لفهم الزمر فهمًا يتجاوز مجرد المعالجات الرمزية كما فُعل أعلاه، يجب استخدام مفاهيم أكثر بنيوية.^6[›] يوجد مبدأ مفهومي تقوم عليه كل المفاهيم الآتية، وهو استغلال الخصائص البنيوية الفريدة للزمر (والتي ليست في المجموعات)، ويجب للبنى المرتبطة بالزمر التلاؤم مع عمليتها. يتجلى هذا التلاؤم في المفاهيم التالية بطرق مختلفة، فمثلًا يمكن للزمر أن ترتبط مع بعضها البعض بدوال تُعرف بتشاكلات الزمر، ووفقًا للمبدأ المفهومي المذكور آنفًا، فإنه يتعين على هذه الدوال أن تُعنى ببنى الزمر بالمعنى الدقيق. ومن الممكن أيضًا فهم الزمر بنيةً من خلال تقسيمها إلى أجزاء تُعرف بالزمر الجزئية وزمر خارج القسمة. إن مبدأ «الحفاظ على البنى» هو موضوع متكرر في الرياضيات كافة، وهو يستدعي بحد ذاته العمل في فئة، وهي في حالة الزمر تُدعى فئة الزمر.

تشاكلات الزمر

تشاكلات الزمر^7[›] هي دوال تحفظ بنية الزمرة. وتُسمى الدالة ${\displaystyle a\colon G\!\rightarrow H\!}$  بين الزمرتين ${\displaystyle (G\!,\bullet )}$  و ${\displaystyle (H,*)}$  تشاكلًا إذا تحققت المعادلة ${\displaystyle 1=a(g\bullet k)=a(g)*a(k)}$  لكل عنصرين ${\displaystyle g}$  و ${\displaystyle k}$  في ${\displaystyle G\!}$ . وبعبارة أخرى، لا يتغير الناتج عند القيام بعملية الزمرة قبل أو بعد التطبيق ${\displaystyle a}$ . وينتج عن هذا الشرط أن ${\displaystyle a(1_{G\!})=1_{H\!}}$ ، وأن ${\displaystyle a(g)^{-1}=a(g^{-1})}$  لكل ${\displaystyle g}$  في ${\displaystyle G\!}$ . وبالتالي فإن تشاكل الزمرة يُعنى ببنية ${\displaystyle G\!}$  كاملةً والتي تتمثل في بديهيات الزمر.

تُوصف الزمرتان ${\displaystyle G\!}$  و ${\displaystyle H\!}$  بأنهما متساويتا الشكل إذا كان كلا التطبيقين ${\displaystyle a\colon G\!\rightarrow H\!}$  و ${\displaystyle b\colon H\!\rightarrow G\!}$  تشاكلًا، أي أن تطبيق كلتا الدالتين الواحدة تلو الأخرى في كلا الترتيبين الممكنين يُعطي الدالتين المحايدتين في ${\displaystyle G\!}$  و ${\displaystyle H\!}$ . أي أن ${\displaystyle a(b(h))=h}$  و ${\displaystyle b(a(g))=g}$  لأي ${\displaystyle g}$  في ${\displaystyle G\!}$  و ${\displaystyle h}$  في ${\displaystyle H\!}$ .

من وجهة نظر تجريدية، تحمل الزمر المتشابهة شكليًّا نفس المعلومات، فمثلًا يكون إثبات أن ${\displaystyle g\bullet g=1_{G\!}}$  لعنصر ما ${\displaystyle g}$  من ${\displaystyle G\!}$  يُكافئ إثبات أن ${\displaystyle a(g)*a(g)=1_{H\!}}$ ؛ لأن تطبيق الدالة ${\displaystyle a}$  على المتساوية الأولى يعطي الثانية، وتطبيق الدالة ${\displaystyle b}$  على الثانية يُعيدها إلى الأولى.

الزمر الجزئية

إن الزمرة الجزئية ببساطة هي زمرة ${\displaystyle H\!}$  موجودة في زمرة أكبر ${\displaystyle G\!}$ . ويكون العنصر المحايد للزمرة ${\displaystyle G\!}$  موجودًا عمليًّا ضمن الزمرة ${\displaystyle H\!}$ ، وعندما يكون ${\displaystyle h_{1}}$  و ${\displaystyle h_{2}}$  في ${\displaystyle H\!}$ ، يكون ${\displaystyle h_{1}\bullet h_{2}}$  و ${\displaystyle h_{1}^{-1}}$  أيضًا في ${\displaystyle H\!}$ ، وبذلك تشكل عناصر ${\displaystyle H\!}$  مزودةً بعملية الزمرة ${\displaystyle G\!}$  المقصورة على ${\displaystyle H\!}$  زمرةً جزئية.

في مثال الزمرة ${\displaystyle D\!_{4}}$  المذكور أعلاه، يشكل المحايد والدورانات زمرة جزئية ${\displaystyle R\!=\{id,r_{1},r_{2},r_{3}\}}$ ، وهي مظللة باللون الأحمر في الجدول أعلاه؛ حيث أن أي دورانين مركبين يشكلان دورانًا أيضًا، وكل دوران يمكن إبطاله بدوران آخر (أي العنصر المعاكس) هو الدوران الذي يشكل مع الدوران الأصلي دورة كاملة: 270° مع 90°، و 180° مع 180°، و 90° مع 270° (لاحظ أن الدوران في الاتجاه المعاكس غير معرف). إن اختبار الزمرة الجزئية شرط ضروري وكاف للمجموعة الجزئية ${\displaystyle H\!}$  من الزمرة ${\displaystyle G\!}$  لتكون زمرة؛ حيث يكفي التأكد من أن ${\displaystyle g^{-1}h\in H\!}$  لكل ${\displaystyle g,h\in H\!}$ . كما أن معرفة الزمر الجزئية مهم في فهم الزمرة كليةً.^8[›]

بإعطاء أي مجموعة جزئية ${\displaystyle S\!}$  من زمرة ${\displaystyle G\!}$ ، تتكون الزمرة الجزئية التي تولدها ${\displaystyle S\!}$  من نواتج إخضاع عناصر ${\displaystyle S\!}$  لعملية الزمرة مع بعضها البعض، بالإضافة إلى معكوسات تلك النواتج. وهي أصغر زمرة جزئية من ${\displaystyle G\!}$  تضم ${\displaystyle S\!}$ . وفي المثال المقدم أعلاه، تتكون الزمرة الجزئية المولدة بـ ${\displaystyle r_{2}}$  و ${\displaystyle f_{v}}$  من هذين العنصرين، والعنصر المحايد، والعنصر ${\displaystyle f_{h}=f_{v}\bullet r_{2}}$ . ومجددًا هذه زمرة جزئية؛ لأن تركيب أي عنصرين من تلك العناصر الأربعة أو معكوساتها (والتي هي ذات تلك العناصر في هذه الحالة الخاصة) ينتج عنصرًا ينتمي إلى هذه الزمرة الجزئية.

المجموعات المشاركة

من المستحسن في العديد من الحالات أن يُعَد عنصران في الزمرة نفسيهما إن اختلفا بعنصر من زمرة جزئية معطاة. فمثلًا في مثال الزمرة ${\displaystyle D\!_{4}}$  المعطى أعلاه، بمجرد تأدية انعكاس ما، لا يعود المربع إلى وضع ${\displaystyle r_{2}}$  بالقيام بعمليات الدوران، أي أن عمليات الدوران ليست ذات صلة بسؤال ما إذا كان قد أُجري انعكاس. تستخدم المجموعات المشاركة لتناول هذه الرؤية تناولًا رسميًّا: تحدد المجموعة الجزئية ${\displaystyle H\!}$  مجموعة مشاركة يمنى وأخرى يسرى، والتي يمكن وصفهما انزلاقين لـ${\displaystyle H\!}$  بأي عنصر من عناصرها ${\displaystyle g}$ . ويعبَّر عن المجموعتين المشاركتين اليسرى واليمنى لـ ${\displaystyle H\!}$  التي تحتوي العنصر ${\displaystyle g}$  كالتالي:

${\displaystyle gH\!=\{g\bullet h\colon h\in H\!\}}$  و ${\displaystyle H\!g=\{h\bullet g\colon h\in H\!\}}$  بالترتيب.

تشكل المجموعات المشاركة لأي زمرة جزئية ${\displaystyle H\!}$  تجزئة لـ ${\displaystyle G\!}$ ، بمعنى أن اتحاد كل المجموعات المشاركة اليسرى يساوي ${\displaystyle G\!}$ ، وتكون كل مجموعتين يسريين إما متساويتين أو غير متقاطعتين. تحدث الحالة الأولى ${\displaystyle g_{1}H\!=g_{2}H\!}$  إذا وفقط إذا كان ${\displaystyle g_{1}^{-1}\bullet g_{2}\in H\!}$ ، أي إذا اختلف العنصران بعنصر من ${\displaystyle H\!}$ ، وما قيل في المجموعات المشاركة اليسرى ينطبق على المجموعات المشاركة اليمنى لـ ${\displaystyle H\!}$ . ومن الممكن أن تتساوى المجموعتان المشاركتان اليسرى واليمنى ومن الممكن أن لا تتساويا، فإذا تساويتا (أي إذا كان ${\displaystyle gH\!=H\!g}$  لكل ${\displaystyle g\in H\!}$ )، تسمى ${\displaystyle H\!}$  حينها زمرة جزئية طبيعية.

في الزمرة ${\displaystyle D\!_{4}}$  المقدمة مثالًا لزمرة التماثل، المجموعات المشاركة اليسرى ${\displaystyle gR\!}$  للزمرة الجزئية ${\displaystyle R\!}$  المكونة من الدورانات إما أن تساوي ${\displaystyle R\!}$  إذا كان ${\displaystyle g}$  عنصرًا من ${\displaystyle R\!}$  نفسها، أو أن تساوي ${\displaystyle U\!=f_{c}R\!=\{f_{c},f_{v},f_{d},f_{h}\}}$  (المظللة باللون الأخضر). كما أن ${\displaystyle R\!}$  زمرة جزئية طبيعية، لأن ${\displaystyle f_{c}R\!=U\!=R\!f_{c}}$  والأمر ينطبق على أي عنصر غير ${\displaystyle f_{c}}$ .

زمرة خارج القسمة

في بعض الحالات يمكن منح قانون زمرة لمجموعة المجموعات المشاركة لزمرة جزئية ما، وينتج عن ذلك ما يُعرف بزمرة خارج القسمة. ويجب أن تكون هذه الزمرة الجزئية طبيعيةً ليكون ذلك بالإمكان. بإعطاء أي زمرة جزئية طبيعية ${\displaystyle N\!}$ ، تحدَّد زمرة خارج القسمة بالتالي

${\displaystyle G\!/N\!=\{gN\!\colon g\in G\!\}(G\!\,\operatorname {modulo} \,N\!)}$ 

تأخذ هذه المجموعة عمليتها (وتُدعى عادةً ضرب أو جمع المجموعات المشاركة) من الزمرة الأصلية ${\displaystyle G\!}$ . ${\displaystyle (gN\!)(hN\!)=(gh)N\!}$  لكل ${\displaystyle g}$  و ${\displaystyle h}$  في ${\displaystyle G\!}$ . يُدعم هذا التعريف بفكرة تمثل النظرات البنيوية العامة المحدَّدة سابقًا، وهي أن التطبيق ${\displaystyle G\!\rightarrow G\!/N\!}$  الذي يربط إلى كل عنصر ${\displaystyle g}$  مجموعته المشاركة ${\displaystyle gN\!}$  يكون تشاكلًا، أو بالتعبير المجرد العام يسمى الخصائص الشاملة. والمحايد في هذه الزمرة يتمثل في المجموعة المشاركة ${\displaystyle eN\!=N\!}$ ، ومعاكس ${\displaystyle gN\!}$  في زمرة خارج القسمة هو ${\displaystyle (gN\!)^{-1}=(g^{-1})N\!}$ .^9[›]

•	R	U
R	R	U
U	U	R
جدول الزمرة لزمرة خارج القسمة ${\displaystyle D\!_{4}/R\!}$ .

عناصر زمرة خارج القسمة ${\displaystyle D\!_{4}/R\!}$  هي ${\displaystyle R\!}$  نفسها والتي تمثل المحايد، ومعها ${\displaystyle U\!=f_{v}R\!}$ . يعرض الجدول على اليسار عملية زمرة خارج القسمة. فمثلًا ${\displaystyle U\!\bullet U\!=f_{v}R\!\bullet f_{v}R\!=(f_{v}\bullet f_{v})R\!=R\!}$ . إن كلًّا من الزمرة الجزئية ${\displaystyle R\!=\{id,r_{1},r_{2},r_{3}\}}$  بالإضافة إلى خارج القسمة المقابل أبيليان، وهذا رغم أن ${\displaystyle D\!_{4}}$  ليست أبيلية. إن بناء زمر أكبر من أخرى أصغر كبناء الزمرة ${\displaystyle D\!_{4}}$  من الزمرة الجزئية ${\displaystyle R\!}$  وخارج القسمة ${\displaystyle D\!_{4}/R\!}$  يجرَّد بمفهوم يسمى الجداء شبه المباشر.

تشكل زمر خارج القسمة والزمر الجزئية معًا طريقةً لوصف أي زمرة من خلال تباديلها: أي زمرة هي خارج قسمة للزمرة الحرة على مولدات الزمرة، وهي خارج قسمة زمرة العلاقات الجزئية. فمثلًا يمكن توليد الزمرة الزوجية ${\displaystyle D\!}$  بعنصرين ${\displaystyle r}$  و ${\displaystyle f}$  (وعلى سبيل المثال: ${\displaystyle r=r_{1}}$  أي الدوران بزاوية قائمة، و ${\displaystyle f=f_{v}}$  أي الانعكاس العمودي (أو أي انعكاس آخر))، ما يعني أن كل تماثل للمربع هو تركيب منتهٍ من هذين التماثلين أو معكوسهما. وإلى جانب هذه العلاقات

${\displaystyle r^{4}=f^{2}=(r\bullet f)^{2}=1}$ ،

تُوصف الزمرة وصفًا كاملًا. ويمكن استخدام توصيف الزمرة أيضًا في إنشاء مبيان كيلي، وهو وسيلة تستخدم لتمثيل الزمر المتقطعة.

ترتبط زمر خارج القسمة والزمر الجزئية على النحو التالي: يمكن النظر إلى المجموعة الجزئية ${\displaystyle H\!}$  من ${\displaystyle G\!}$  على أنها تطبيق تبايني ${\displaystyle H\!\rightarrow G\!}$ ، أي أن أي عنصر من المجال المقابل يرتبط بعنصر واحد على الأكثر. كما يوجَد ما يُعرف بالتطبيقات الشمولية، وهو تطبيق ترتبط فيه كل عناصر المجال المقابل بعنصر أو أكثر من المجال، مثل التطبيق ${\displaystyle G\!\rightarrow G\!/N\!}$ .^10[›] إن تفسير الزمر الجزئية وخوارج القسمة في ضوء هذه التشاكلات يؤكد على المفهوم البنيوي الملازم لتلك التعريفات المشار إليها في المقدمة. ليست التشاكلات عمومًا متباينة ولا شمولية. ويعالج هذه الظاهرة كل من نواة وصورة تشاكلات الزمرة ومبرهنة تساوي الشكل الأولى.

 

ثمة نمط دوري في ورق الحائط ينبثق عنه زمرة ورق الحائط.

 

تتكون الزمرة الأساسية لمستوًى ما ناقص نقطة (غليظة) من الحلقات حول تلك النقطة. وتلك الزمرة الأساسية هي مساوية الشكل للأعداد الصحيحة.

تكثر الأمثلة على الزمر وتطبيقاتها، وقد كانت زمرة ${\displaystyle \mathbb {Z\!} }$  للأعداد الصحيحة تحت عملية الجمع عمليةً للزمرة أولَ مثال شُرح أعلاه. وإذا أُخذت عملية الضرب عمليةً للزمرة بدل الجمع، تصبح الزمرة زمرة ضربية. وتعد تلك الزمرتان سلفًا لبنًى مهمة في الجبر المجرد.

تطبَّق الزمر في مجالات عديدة من الرياضيات. كثيرًا ما تُفحص الكائنات الرياضية بتجميع زمر إليها ودراسة خصائص الزمر المناظرة. فمثلًا قام هنري بوانكاريه بتأسيس ما نسميه الآن الطوبولوجيا الجبرية بإدخاله الزمر الأساسية إلى الطوبولوجيا. وقد تُرجمت في هذا السياق عدد من الخصائص الطوبولوجية مثل القرب والاستمرارية إلى خصائص للزمر.^11[›] فمثلًا تمثَّل الزمرة الأساسية بالحلقات. توضح الصورة الثانية على اليسار بعض الحلقات في مستوًى ما ناقص نقطة. تعد الحلقة الزرقاء مثلية التوضع فراغيا (وهي بالتالي ليست موضع اهتمامنا)، وذلك لأنها يمكن أن تتقلص باستمرار إلى نقطة. إن وجود الثقب يَحول دون تقلص الحلقة البرتقالية إلى نقطة. تتحول الزمرة الأساسية لمستوًى ما إلى زمرة دائرية غير منتهية عند محو نقطة من هذا المستوى، وتكون مولَّدة بالحلقة البرتقالية أو أي حلقة أخرى تلف مرة واحدة حول الثقب). وبالتالي تعَد الزمرة الأساسية كاشفًا لوجود الثقب.

في التطبيقات الأكثر حداثة للزمر، كان التأثير موجَّهًا أيضًا نحو دعم الإنشاءات الهندسية بخلفية نظرية زمرية.^12[›] وفي المقابل، توظف نظرية الزمر الهندسية مفاهيمَ هندسية لدراسة الزمر الزائدية مثلًا. وتوجَد فروع أخرى تطبق الزمر تطبيقًا أكثر تأثيرًا، منها الهندسة الجبرية ونظرية الأعداد.

يوجَد العديد من التطبيقات العملية للزمر بالإضافة إلى التطبيقات النظرية السابقة. مثلًا يقوم علم التعمية على مزيج من النهج النظري الزمري المجرَّد والمعرفةالخوارزمية المستمَدة من نظرية الزمر الحوسبية، خاصة عند تطبيقها لزمر منتهية. ولا تنحصر تطبيقات نظرية الزمر في الرياضيات؛ فعلوم مثل الفيزياء وكيمياء وعلم الحاسوب تنتفع من أفكارها.

الأعداد

تتمتع العديد من النظم العددية كالأعداد الصحيحة والكسرية ببنية زمرية مرتبطة بطبيعتها. تنبثق عن عمليتي الجمع والضرب بنًى زمرية في بعض الحالات كما في الأعداد الكسرية. وتُعد مثل تلك النظم العددية أسلافًا لبنًى جبرية أعم معروفة بالحلقات والحقول. ويشكل المزيد من الفكر الجبرية المجردة زمرًا، ومنها النماذج والفضاءات المتجهية والجِبار.

الأعداد الصحيحة

لقد وُصفت سابقًا في المقالة زمرة الأعداد الصحيحة ${\displaystyle \mathbb {Z\!} }$  تحت عملية الجمع ورمزها ${\displaystyle (\mathbb {Z\!} ,+)}$ . ورغم ذلك لا تشكل الأعداد الصحيحة زمرة تحت الضرب بدل الجمع ${\displaystyle (\mathbb {Z\!} ,\cdot )}$ ؛ إذ أنه رغم توافر بديهيات الانغلاق والتجميعية ووجود المحايد، لا تتوافر بديهية وجود المعاكس في هكذا بنية. فمثلًا ${\displaystyle a=2}$  هو عدد صحيح، لكن الحل الوحيد للمعادلة ${\displaystyle a\cdot b=1}$  في تلك الحالة هو ${\displaystyle b={\frac {1}{2}}}$ ، وهو كسري وليس صحيحًا. وبالتالي ليس كل عنصر من ${\displaystyle \mathbb {Z\!} }$  يملك معاكسًا ضربيًّا.^13[›]

الأعداد الكسرية

إن الرغبة في وجود المعاكسات الضربية توحي بفكرة الكسور

${\displaystyle {\frac {a}{b}}}$ .

وتُعرف كسور الأعداد الصحيحة (حيث ${\displaystyle b\neq 0}$ ) بالأعداد الكسرية.^14[›] ويُرمز للمجموعة التي تحتوي كل هذه الكسور بالرمز ${\displaystyle \mathbb {Q\!} }$ . لكن ما زالت هناك عقبة تَحُول دون كون الأعداد الكسرية تحت عملية الضرب ${\displaystyle (\mathbb {Q\!} ,\cdot )}$  زمرة، وهي أن العدد الكسري 0 لا يملك معكوسًا ضربيًّا (أي أنه لا يوجَد ${\displaystyle x\in \mathbb {Q\!} }$  يحقق المعادلة ${\displaystyle x\cdot 0=1}$ )، وبالتالي لا تزال ${\displaystyle (\mathbb {Q\!} ,\cdot )}$  ليست زمرة.

ورغم ذلك، تشكل مجموعة كل الأعداد الكسرية غير الصفرية ${\displaystyle \mathbb {Q\!} \backslash \{0\}=\{q\in \mathbb {Q\!} |q\neq 0\}}$  زمرة أبيلية تحت الضرب، ورمزها هو ${\displaystyle (\mathbb {Q\!} ,\cdot )}$ .^15[›] تنتُج بديهيتا التجميعية والعنصر المحايد عن خصائص الأعداد الصحيحة. كما أن بديهية الانغلاق لم تزل محقَّقة بعد إزالة الصفر، لأن حاصل ضرب أي عددين كسريين غير صفريين لا يساوي أبدًا الصفر. وأخيرًا، العدد الكسري ${\displaystyle {\frac {a}{b}}}$  له معكوس هو ${\displaystyle {\frac {b}{a}}}$ ، وبالتالي تتحقق بديهية الانغلاق في تلك البنية.

تشكل الأعداد الكسرية (متضمنة الصفر) زمرة أيضًا تحت عملية الجمع. وتتضافر عمليتا الجمع والضرب مسفرةً عن بنًى أعقد تُسمى الحلقات، كما تسفر عن ما يُسمى الحقول إذا كانت القسمة ممكنة كما في حالة ${\displaystyle \mathbb {Q\!} }$ ، ولكلا البنيتين موقع محوري في الجبر المجرد. ولذلك فإن حجج نظرية الزمر تكمن وراء أجزاء من نظرية كلا الكيانين.^16[›]

الحساب النمطي

 

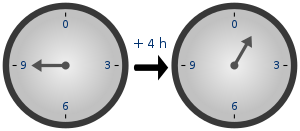
في الحساب النمطي، يُجمَع عددان صحيحان ثم يُقسَم الناتج على عدد صحيح موجب يسمى القيمة النمطية (modulus). ويكون ناتج الجمع النمطي هو باقي تلك القسمة. لأي قيمة نمطية ${\displaystyle n}$ ، تشكل مجموعة الأعداد الصحيحة من الصفر حتى ${\displaystyle n-1}$  زمرةً تحت الجمع النمطي؛ حيث يكون معاكس أي عنصر ${\displaystyle a}$  هو ${\displaystyle n-a}$ ، والعنصر المحايد هنا هو الصفر. ومن المألوف من جمع الساعات في ساعة بنظام 12 ساعة، أنه إذا كان عقرب الساعات على 9 ثم تقدم 4 ساعات، سيصبح على الساعة 1 كما هو موضح على اليسار. ويعبَّر عن ذلك بقول أن 9 + 4 يساوي 1 مقياس 12 أو بتردد 12، أو بالرموز

${\displaystyle 9+4\equiv 1\operatorname {modulo} \,12}$ .

ويُرمَز لزمرة الأعداد الصحيحة مقياس ${\displaystyle n}$  بأحد الرمزين ${\displaystyle \mathbb {Z\!} _{n}}$  أو ${\displaystyle \mathbb {Z\!} /nZ\!}$ .

توجد أيضًا زمرة ضربية للأعداد الصحيحة مقياس ${\displaystyle {\color {Blue}p}}$  لأي عدد أولي ${\displaystyle p}$ . وعناصر تلك الزمرة هي الأعداد الصحيحة من ${\displaystyle 1}$  إلى ${\displaystyle p-1}$ . وعمليتها هي الضرب مقياس ${\displaystyle p}$ ، أي أن حاصل الضرب العادي يُقسَم على ${\displaystyle p}$ ، ويكون باقي تلك القسمة هو ناتج الضرب النمطي. فمثلًا إذا كان ${\displaystyle p=5}$ ، سيوجَد في الزمرة أربعة عناصر هي 1، 2، 3، 4. وفي هذه الزمرة يكون ${\displaystyle 4\cdot 4=1}$ ، لأن حاصل الضرب العادي هو 16 وهو يكافئ 1، وهو باقي قسمة هذا العدد على 5، فالعدد 5 هو قاسم لـ ${\displaystyle 16-1=15}$ ، ويُرمَز لما سبق بالآتي

${\displaystyle 16\equiv 1({\bmod {\,}}5)}$ .

وتكفل أولية العدد ${\displaystyle p}$  أنه إذا ضُرِب عددان صحيحان لا يقبلان القسمة على ${\displaystyle p}$ ، لن يقبل حاصل الضرب القسمة على ${\displaystyle p}$  أيضًا، وبالتالي فإن مجموعة الأصناف المُشار إليها مغلَقة تحت الضرب.^17[›] والعنصر المحايد هو 1 كما هو معتاد لأي زمرة ضربية، وتنتج التجميعية عن الخاصية المناظرة في الأعداد الصحيحة. وأخيرًا تتطلب بديهية العنصر المعاكس أنه بإعطاء العدد الصحيح ${\displaystyle a}$  الذي لا يقبل القسمة على ${\displaystyle p}$ ، يوجد عدد صحيح ${\displaystyle b}$  بحيث يكون

${\displaystyle a\cdot b\equiv 1({\bmod {\,}}p)}$ ، أي أن ${\displaystyle p}$  تقسم الفرق ${\displaystyle a\cdot b-1}$ .

ويمكن إيجاد المعاكس ${\displaystyle b}$  باستخدام متطابقة بوزو وحقيقة أن القاسم المشترك الأكبر ${\displaystyle \gcd(a,p)}$  يساوي 1. وفي حالة ${\displaystyle p=5}$  أعلاه، يكون معاكس 4 هو 4، ومعاكس 3 هو 2؛ لأن ${\displaystyle 3\cdot 2=6\equiv 1({\bmod {\,}}5)}$ . وبالتالي فإن كل بديهيات الزمر محقَّقة. إن هذا المثال في الواقع مشابه لمثال ${\displaystyle (\mathbb {Q\!} \backslash \{0\},\cdot )}$  أعلاه؛ فهو يتكون بالضبط من تلك العناصر في ${\displaystyle \mathbb {Z\!} /p\mathbb {Z\!} }$  التي تملك معاكسًا ضربيًّا. يُرمَز لتلك الزمر بالرمز ${\displaystyle \mathbb {F\!} _{p}^{\times }}$ . وهي بالغة الأهمية في التشفير باستخدام المفتاح المعلن.^18[›]

الزمر الدائرية

 

الزمرة الدائرية هي زمرة كل عناصرها هي قوى لعنصر ما ${\displaystyle a}$ . وباستخدام رموز الضرب، يُعبَر عن عناصر تلك الزمرة كالتالي:

${\displaystyle ...,a^{-3},a^{-2},a^{-1},a^{0}=e,a,a^{2},a^{3},...}$ 

حيث ${\displaystyle a^{2}}$  يعني ${\displaystyle a\bullet a}$ ، و ${\displaystyle a^{-3}}$  يعني ${\displaystyle a^{-1}\bullet a^{-1}\bullet a^{-1}=(a\bullet a\bullet a)^{-1}}$ ، إلى آخره.^19[›] يسمى مثل العنصر ${\displaystyle a}$  مولِّدًا أو عنصرًا بدائيًّا للزمرة. وبرموز الجمع، يكون شرط كون العنصر بدائيًّا أن يكون كل عنصر في الزمرة قابلًا للكتابة على صورة

${\displaystyle ...,-a-a,-a,0,a,a+a,...}$ 

في الزمر ${\displaystyle \mathbb {Z\!} /n\mathbb {Z\!} }$  المشروحة أعلاه، العنصر ${\displaystyle 1}$  هو عنصر بدائي، ما يجعل تلك الزمر دائرية. يمكن التعبير عن كل عنصر في تلك الزمرة في شكل مجموعٍ كلُّ حدوده هي ${\displaystyle 1}$ . وأي زمرة دائرية ذات العدد ${\displaystyle n}$  من العناصر هي مساوية الشكل لتلك الزمرة. وتعد زمرة جذور الوحدة العقدية من الدرجة ${\displaystyle n}$  مثالًا آخر للزمر الدائرية، وهي معطاة بالأعداد العقدية ${\displaystyle z}$  التي تحقق المعادلة ${\displaystyle z^{n}=1}$ . ويمكن تصور تلك الأعداد رؤوسًا لمضلع منتظم ذي عدد ${\displaystyle n}$  من الأضلاع كالموضح بالأزرق في الصورة، والذي فيه ${\displaystyle n=6}$ . وعملية تلك الزمرة هي جداء الأعداد العقدية. وكما توضح الصورة، يقابل الضرب في ${\displaystyle z}$  دورانًا بزاوية 60° عكس اتجاه عقارب الساعة. وبالاستعانة ببعض من نظرية الحقول (الرياضيات)، يمكن للزمرة ${\displaystyle \mathbb {F\!} _{p}^{\times }}$  أن تبدو دائرية: فمثلًا إذا كانت ${\displaystyle p=5}$ ، فإن ${\displaystyle 3}$  مولد في تلك الزمرة؛ لأن ${\displaystyle 3^{1}=3}$ ، و ${\displaystyle 3^{2}=9\equiv 4}$ ، و ${\displaystyle 3^{3}\equiv 2}$ ، و ${\displaystyle 3^{4}\equiv 1}$ .

تملك بعض الزمر الدائرية عددًا غير منتهٍ من العناصر. ولكل عنصر غير مساو للصفر ${\displaystyle a}$  في تلك الزمرة، تكون كل قوى ${\displaystyle a}$  مختلفة عن بعضها البعض؛ وبالتالي فعلى الرغم من كون هكذا زمر «دائرية» إلا أنها لا تدور. وتكون أي زمرة دائرية غير منتهية مساوية الشكل لزمرة الأعداد الصحيحة تحت عملية الجمع ${\displaystyle (\mathbb {Z\!} ,+)}$  المشروحة أعلاه. وكل الزمر الدائرية أبيليةٌ كما رأينا في المثالين السابقين.

بلغت دراسة الزمر الأبيلية منتهية التوليد درجة كبيرة من النضوج، وهي تتضمن المبرهنة الأساسية للزمر الأبيلية منتهية التوليد، ويوجَد الكثير من المفاهيم المتعلقة بالزمر مثل المركز والمبادل تصف إلى أي مدى تكون زمرة ما غير أبيلية.

زمر التماثل

زمر التماثل هي زمر تتكون من تناظرات كائنات هندسية معينة ذات طبيعة هندسية (كزمرة التماثل للمربع المشروحة سابقًا) أو جبرية (مثل المعادلات كثيرة الحدود وحلولها). ومن الناحية النظرية، يمكن أن تعَد نظرية الزمر دراسةً للتناظر.^20[›] تبسط التناظرات في الرياضيات دراسةَ الكائنات الهندسية والتحليلية تبسيطًا بالغًا. يُقال عن زمرة ما أنها تؤثر على كائن رياضي آخر ${\displaystyle X\!}$  إذا كان كل عنصر للزمرة يؤدي عملية ما على ${\displaystyle X\!}$  بالانسجام مع قانون الزمرة. وكما في المثال أدناه، فإن عنصرًا من الرتبة 7 من زمرة المثلث (2,3,7) يؤثر على التبليط بتبديل المثلثات الملتوية المظللة (والمثلثات الأخرى أيضًا). يرتبط نمط الزمرة المؤثرة ببنية الكائن المتأثر من خلال تأثير الزمرة.

 

في حقول الكيمياء كعلم البلورات، تصف الزمر الفراغية والزمر النقطية التناظراتِ الجزيئيةَ والبلورية. تكمن تلك التناظرات وراء السلوك الفيزيائي والكيميائي لتلك الأنظمة، وتتيح نظرية الزمر تبسيط التحليل الميكانيكي الكمومي لتلك الخصائص. مثلًا تستخدَم نظرية الزمر لتوضيح أن الانتقالات البصرية بين المستويات الكمومية لا يمكن أن يحدث ببساطة بسبب تناظر الحالات المعنية.

ليست الزمر مفيدة في تقييم الآثار الناتجة عن التناظرات في الجزيئات فحسب، ولكن من المدهش أنها تتنبأ أيضًا بأنه يمكن للجزيئات في بعض الأحيان أن تغير من تناظرها. تأثير جان-تيلر هو تشويه جزيء ذي تناظر عالٍ عندما يتخذ حالة قاعية ما ذات تناظر أقل من مجموعة الحالات القاعية الممكنة المرتبطة ببعضها من خلال عمليات التناظر للجزيء.

وبالمثل تساعد نظرية الزمر في التنبؤ بالتغيرات في الخصائص الفيزيائية التي تنجم عن خضوع مادة ما لتحول طوري، كتحول المادة مثلًا من الشكل البلوري المكعبي إلى رباعي السطوح. وتعد المواد الفيروكهربية مثالًا على ذلك؛ حيث يحدث التغير من الحالة الباراكهربية إلى الحالة الكهربية الحديدية في درجة حرارة كوري، وهو مرتب بتغير من الحالة الباراكهربية عالية التناظر إلى الحالة الفيروكهربية الأقل تناظرًا، ويكون ذاك التغيير مصحوبًا بما يسمى نمط فونون لينًا، وهو نمط شبكية اهتزازية يصل فيه التردد إلى الصفر خلال الانتقال.

إن لهذا وأمثالِه من طرق كسر التناظر التلقائي المزيدَ من التطبيقات في فيزياء الجسيمات الابتدائية، حيث أن حدوثهم مرتبط بظهور بوزونات جولدستون.

يُظهِر البكمنسترفلورين تناظرًا عشروني السطوح.	الأمونيا NH3. زمرة تماثله من الرتبة 6، وهي مولَّدة بدوران بزاوية 120° وانعكاس واحد.	الكوبان C8H8 يتميز تناظر ثماني السطوح.	أيونات النحاس سداسية الإماهة (II) [Cu(OH2)6]2+ وهي أيونات معقدة. وبمقارنة الجزيء بشكل تام التناظر، يلاحَظ أن الأول متوسع عموديًّا بحوالي 22% (تأثير جان-تيلر).	زمرة المثلث (2,3,7) الزائدية تؤثر على تبليط المستوى الزائدي الذي في الصورة.

تُستَخدم زمر التماثل المنتهية مثل زمرة ماتيو في نظرية الترميز، والمطبَّقة بدورها في تصحيح الخطأ للبيانات المنقولة، كما تُطبَّق زمرة ماتيو في أجهزة السي دي. وتعد نظرية غالوا التفاضلية تطبيقًا آخر لزمر التماثل، وهي تصف الدوال ذات المشتقات العكسية، معطيةً معايير نظرية زمرية لكون حلول معادلات تفاضلية معينةٍ مهذبةً.^21[›] ثم إن الخصائص الهندسية التي تبقى مستقرة تحت تأثيرات الزمرة يُحقَّق بشأنها في النظرية الثابتة الهندسية.

الزمر الخطية العامة ونظرية التمثيل

 

تتكون زمرة المصفوفات من مصفوفات مع عملية ضرب المصفوفات. الزمرة الخطية العامة ${\displaystyle G\!L\!(n,R\!)}$  مكونة من كل المصفوفات من الرتبة ${\displaystyle n\times n}$  ذات المعكوس والمكونة من مدخلات حقيقية. ويطلق على زمرها الجزئية زمر المصفوفات أو الزمر الخطية. ويمكن أن تعد الزمرة الزوجية المشروحة أعلاه زمرةَ مصفوفات بالغة الصغر. وكذا تعد الزمرة المتعامدة الخاصة ${\displaystyle S\!O\!(n)}$  زمرةَ مصفوفات مهمة أخرى. وهي تصف كل الدورانات الممكنة في العدد ${\displaystyle n}$  من الأبعاد. تُستَخدم مصفوفات الدوران في الرسوميات الحاسوبية بواسطة زوايا أويلر.

نظرية التمثيل هي تطبيق لمفهوم الزمرة، كما أنها ضرورية للوصول إلى فهم أعمق للزمر. ويختص العاملون فيها بدراسة الزمرة من خلال تأثيراتها على الفضاءات الأخرى. وتشكل التمثيلات الخطية فئة كبيرة من تمثيلات الزمر، وهي الناجمة عن تأثير الزمرة على فضاء متجهي كالفضاء الإقليدي ثلاثي الأبعاد ${\displaystyle R\!^{3}}$ . إن أي تمثيل للزمرة ${\displaystyle G\!}$  على فضاء متجهي حقيقي بعدد ${\displaystyle n}$  من الأبعاد هو ببساطة تشاكل زمري

${\displaystyle \rho \colon G\!\rightarrow G\!L\!(n,R\!)}$ 

من الزمرة إلى الزمرة الخطية العامة. وهكذا تتحول عملية الزمرة (المعطاة تجريديًّا) إلى ضرب المصفوفات؛ فتصبح في متناوَل الحسابات الصريحة.^21[›]

يعطي هذا معاني أعمق لدراسة الكائن المؤثَّر عليه بتأثير زمري ما.^22[›] ومن ناحية أخرى، فإنه يعطي أيضا معلومات عن الزمرة. إن تمثيلات الزمر مبدأٌ منظِّم في نظرية الزمر المنتهية وزمر لي والزمر الجبرية والزمر الطوبولوجية وخاصةً الزمر المتراصة (محليًّا).

لقد طُوِّرت زمر غالوا للمساعدة في حل المعادلات كثيرة الحدود من خلال تمثيل خصائصها التناظرية. فمثلًا تكون حلول المعادلة التربيعية ${\displaystyle ax^{2}+c=0}$  معطاةً من خلال

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.}$ 

يمكن النظر إلى المبادلة بين "+" و "-" في التعبير السابق، أي تبديل حلى المعادلة، بمثابة عملية زمرية بسيطة جدًّا. وتوجد صيغ مماثلة معروفة للمعادلات التكعيبية والرباعية، ولكن هذا لا ينطبق عامة على الدرجة الخامسة وما فوقها. الخصائص التجريدية لزمر غالوا المتعلقة بكثيرات الحدود (خاصةً قابليتها للحلحلة) تعطي معيارًا لكثيرات الحدود التي يمكن التعبير عن كافة حلولها بالجذور، أي باستخدام الجمع والضرب والجذور فقط كما في الصيغة أعلاه.

من الممكن التعامل مع تلك المسألة من خلال التحول إلى نظرية الحقل مع النظر في حقل الانشطار لكثيرة الحدود. تعمم نظرية غالوا الحديثة هذا النوع من زمر غالوا المذكور أعلاه إلى امتدادات حقول وتضع—عن طريق المبرهنة الأساسية في نظرية غالوا—علاقة دقيقة بين الحقول والزمر، مما يؤكد مجددًا انتشار الزمر في فروع الرياضيات الأخرى.

يُقال إن الزمرة منتهية إذا امتلكت عدد محدودًا من العناصر. ذلك العدد يطلق عليه رتبة تلك الزمرة. وتعد الزمر المتماثلة ${\displaystyle S\!_{N\!}}$  من أهم أصنافها، وهي زمر تباديل العدد N من الرموز. على سبيل المثال، تتكون الزمرة المتماثلة في ثلاثة رموز ${\displaystyle S\!_{3}}$  من كل التسلسلات الممكنة للحروف اللثلاث ${\displaystyle {ABC}\!}$ ، أي ${\displaystyle {ABC}\!}$  و ${\displaystyle {ACB}\!}$  وهكذا حتى ${\displaystyle {CBA}\!}$ ، وعددها في المجمل 6 (عاملي 3). ويكون هذا الصنف أساسيًّا طالما أن أي زمرة منتهية يمكن التعبير عنها في صورة زمرة جزئية من زمرة متماثلة ${\displaystyle S\!_{N\!}}$  حيث ${\displaystyle N\!}$  عدد صحيح مناسب (مبرهنة كيلي). وكما في زمرة تماثلات المربع المشروحة أعلاه، يمكن تناول الزمرة ${\displaystyle S\!_{3}}$  على أنها زمرة تماثلات مثلث متساوي الأضلاع.

تعرف رتبة العنصر ${\displaystyle a}$  في المجموعة ${\displaystyle G\!}$  بأنها أقل عدد صحيح موجب ${\displaystyle n}$  يحقق أن ${\displaystyle a^{n}=e}$ ، حيث ${\displaystyle a^{n}}$  يمثل

${\displaystyle \underbrace {a\cdots a} _{n{\text{ factors}}},}$ 

أي تطبيق العملية ${\displaystyle \cdot }$  على ${\displaystyle n}$  نُسَخ من ${\displaystyle a}$ ، فإن كانت ${\displaystyle \cdot }$  تمثل الضرب، فإن ${\displaystyle a^{n}}$  يمثل العدد ${\displaystyle a}$  مرفوعًا للأس ${\displaystyle n}$ . في الزمر غير المنتهية قد لا يوجد مثل العدد ${\displaystyle n}$ ، ويُقال حينها إن رتبة ${\displaystyle a}$  هي اللانهاية. وبتعبير آخر، رتبة العنصر في زمرة هي رتبة الزمرة الجزئية الدورية التي يولدها هذا العنصر.

تنتج عن البيانات المتعلقة بالزمر المنتهية طرقٌ أكثر تعقيدًا في العد مثل عد المجموعات المشاركة، ومنها مبرهنة لاغرانج التي تنص على أنه عندما تكون ${\displaystyle G\!}$  زمرة منتهية، تقبل رتبتها القسمة على رتبة أي زمرة جزئية منها ${\displaystyle H\!}$ ، وتثبت مبرهنات سيلو العكس الجزئي لمبرهنة لاغرانج.

تعد الزمرة الزوجية (المشروحة أعلاه) زمرة منتهية من الرتبة 8. رتبة العنصر ${\displaystyle r_{1}}$  تساوي 4؛ حيث أنها أيضًا رتبة الزمرة الجزئية التي يولدها ذلك العنصر ${\displaystyle R\!}$  (انظر أعلاه). ورتبة عناصر الانعكاس (${\displaystyle f_{v}}$  وما علا شاكلته) تساوي 2. وكلتا الرتبتين الأخيرتين تقسم رتبة الزمرة الكبرى وهي 8، وهذا ما أثبتته مبرهنة لاغرانج. وتمتلك الزمر ${\displaystyle \mathbb {F\!} _{p}^{\times }}$  رتبة تساوي ${\displaystyle p-1}$ .

تصنيف الزمر المنتهية البسيطة

غالبًا ما يسعى علماء الرياضيات إلى وضع تصنيف متكامل (أو قائمة) لأي مفهوم رياضي. ويؤدي هذا الهدف إلى معضلات رياضية صعبة فيما يتعلق بالزمر المنتهية. وفقًا لمبرهنة لاغرانج، تكون الزمر المنتهية من الرتبة p (عدد أولي) زمرًا دورية (أبيلية) بالضرورة، ورمزها ${\displaystyle \mathbb {Z} _{p}}$ . يمكن أيضًا للزمر من الرتبة ${\displaystyle p^{2}}$  أن تظهر أبيلية، لكن ذلك لا يشمل الزمر من الرتبة ${\displaystyle p^{3}}$ ، كما يظهر أعلاه في مثال الزمرة ${\displaystyle D\!_{4}}$  ذات الرتبة 8 = 2³. يمكن لنظم الجبر المحوسبة أن تُستخدم لعمل قائمة بالزمر الصغيرة، ولكن لا يوجد تصنيف يشمل كافة الزمر المنتهية.^19[›] لكن أمكن تصنيف الزمر المنتهية البسيطة.^20[›] تسمى الزمر غير التافهة بسيطة إن كان لها زمرتان جزئيتان طبيعيتان لا ثالثة لهما هما الزمرة التافهة والزمرة نفسها.^21[›] تُظهر مبرهنة جوردان-هلدر الزمرَ المنتهية البسيطة في شكل اللبنات الأساسية لكافة الزمر المنتهية. إن وضع قائمة بكافة الزمر المنتهية البسيطة كان إنجازًا رائدًا في نظرية الزمر المعاصرة. نجح العالم ريتشارد بورشردس الحائز على ميدالية فيلدز عام 1998 - في برهنة حدسيات نظرية مونشاين، وهي علاقة مدهشة وعميقة بين أكبر زمرة مشتتة منتهية بسيطة —"زمرة الوحش"—، ودوال نمطية معينة (والدوال النمطية هي جزء من التحليل المركب التقليدي)، ونظرية الأوتار (النظرية التي يُفترض أنها تمثل الوصف الفيزيائي الموحَّد للعديد من الظواهر الفيزيائية).

تعد الكثير من الزمر مثالًا على بنًى رياضية أخرى علاوةً على كونها مثالًا على الزمر، وبلغة نظرية الأصناف فهي تعد كائنات زمرية في الفئة، ما يعني أنها كائنات (أي أمثلة على كائن رياضي آخر) تأتي مع تحويلات تسمى التطبيقات المحافظة على الشكل بحيث تحاكي تلك التحويلاتُ بديهياتِ الزمر. فمثلًا بحسب تعريف الزمر المذكور أعلاه فإن أي زمرة تعد مجموعة أيضًا، لذلك فإن أي زمرة تمثل كائنًا زمريًّا في فئة المجموعات.

زمر طوبولوجية

 

زمر لي

سميت هكذا نسبة إلى عالم الرياضيات سوفوس لي.

• متتالية منضبطة.
• زمرة أبيلية.
• تمثيل زمرة منتهية