Лагарыфм

зв. асно́ву, каб атрымаць значэнне x. Запіс ${\displaystyle \log _{b}a}$ чытаецца як «лагарыфм ${\displaystyle a}$ па аснове ${\displaystyle b}$».

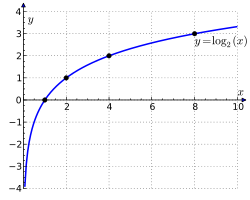
З азначэння вынікае, што знаходжанне ${\displaystyle x=\log _{b}a}$ раўназначнае рашэнню ўраўнення

${\displaystyle b^{x}=a.}$

Напрыклад, лагарыфм 1000 па аснове 10 роўны 3, бо 1000 ёсць 10 у ступені 3: 1000 = 10·10·10 = 10³.

Вылічэнне лагарыфма называецца лагарыфмава́ннем.

Лагарыфмы маюць цікавыя ўласцівасці, якія дазваляюць спрашчаць працаёмкія вылічэнні. Пры пераходзе «ў свет лагарыфмаў» множанне замяняецца на значна прасцейшае складанне, дзяленне — на адыманне, а ўзвядзенне ў ступень і здабыванне кораня ператвараюцца адпаведна ў множанне і дзяленне на паказчык ступені. Лаплас казаў, што вынаходніцтва лагарыфмаў, «скараціўшы працу астранома, падвоіла яго жыццё». У прыкладаннях аснова b лагарыфма і лагарыфмуемы лік (аргумент лагарыфма) звычайна рэчаісныя. Тым не менш, існуе шэраг праблем (у тым ліку і прыкладных), дзе карысным аказваецца так званы камплексны лагарыфм.

Азначэнне лагарыфмаў і табліцу іх значэнняў (для трыганаметрычных функцый) упершыню надрукаваў у 1614 годзе шатландскі матэматык Джон Непер. Лагарыфмічныя табліцы, пашыраныя і ўдакладненыя іншымі матэматыкамі, паўсюдна выкарыстоўваліся ў навуковых і інжынерных разліках больш за тры стагоддзі, пакуль не з’явіліся электронныя вылічальныя машыны.

З цягам часу высветлілася, што лагарыфмічная функцыя ${\displaystyle y=\log _{b}x}$ незаменная і ў шмат якіх іншых галінах чалавечай дзейнасці: развязанні дыферэнцыяльных ураўненняў, вымярэнні фізічных велічынь (напрыклад, частаты і магутнасці гуку), прыбліжэнні розных залежнасцей, тэорыі інфармацыі, тэорыі імавернасцей і г. д. Гэта функцыя ўваходзіць у лік элементарных, лагарыфм адваротны да паказчыкавай функцыі. Часцей за ўсё выкарыстоўваюцца рэчаісныя лагарыфмы па аснове e (натуральны), 10 (дзесятковы) і 2 (двайковы).

Лагарыфм ${\displaystyle x=\log _{b}a}$  па азначэнню ёсць рашэнне ўраўнення

${\displaystyle b^{x}=a.}$ 

Выпадак ${\displaystyle b=1}$  не вельмі цікавы, бо пры ${\displaystyle a\neq 1}$  гэта ўраўненне не мае рашэння, а пры ${\displaystyle a=1}$  любы лік з’яўляецца рашэннем; у абодвух выпадках лагарыфм не вызначаны. Гэтак жа прыходзім да высновы, што лагарыфм не існуе пры нулявым і адмоўным ${\displaystyle b}$ ; акрамя таго, значэнне паказчыкавай функцыі ${\displaystyle b^{x}}$  заўсёды дадатнае, таму варта выключыць і выпадак адмоўнага ${\displaystyle a}$ . Канчаткова атрымліваем:

Як вядома, паказчыкавая функцыя ${\displaystyle y=b^{x}}$  (пры выкананні вышэйзгаданых умоў на ${\displaystyle b}$ ) вызначана, манатонная і кожнае значэнне прымае толькі адзін раз, прычым абсяг яе значэнняў утрымлівае ўсе дадатныя рэчаісныя лікі. Адсюль вынікае, што значэнне рэчаіснага лагарыфма дадатнага ліку заўсёды вызначана і адзінае.

Найбольш шырокі ўжытак і шматлікія дастасаванні маюць наступныя віды лагарыфмаў:

• Натуральны: ${\displaystyle \ln x}$ , аснова: лік Ойлера e.
• Дзесятковы: ${\displaystyle \lg x}$ , аснова: лік 10.
• Двайковы: ${\displaystyle \log _{2}x}$  або ${\displaystyle \operatorname {lb} x}$ , аснова: 2. Яны ўжываюцца, напрыклад, у тэорыі інфармацыі, інфарматыцы, у многіх раздзелах дыскрэтнай матэматыкі.

Уласцівасці

Асноўная лагарыфмічная тоеснасць

З азначэння лагарыфма вынікае асноўная лагарыфмічная тоеснасць:

• ${\displaystyle a^{\log _{a}x}=x}$ 
• ${\displaystyle \log _{a}\left(a^{x}\right)=x}$ 

Вывад: з роўнасці двух рэчаісных лагарыфмаў вынікае роўнасць лагарыфмаваных выразаў. Сапраўды, калі ${\displaystyle \log _{a}b=\log _{a}c}$ , то ${\displaystyle a^{\log _{a}b}=a^{\log _{a}c}}$ , адкуль, адпаведна асноўнай тоеснасці: ${\displaystyle b=c.}$ 

Лагарыфмы адзінкі і ліку, роўнага аснове

• ${\displaystyle \log _{a}1=0,}$ 
• ${\displaystyle \log _{a}a=1.}$ 

Арыфметычныя ўласцівасці лагарыфма

• Лагарыфм здабытку:

${\displaystyle \log _{a}(xy)=\log _{a}(x)+\log _{a}(y)}$ 

• Лагарыфм дзелі:

${\displaystyle \log _{a}\left({\frac {x}{y}}\right)=\log _{a}(x)-\log _{a}(y)}$ 

• Лагарыфм ступені:

${\displaystyle \log _{a}(x^{p})=p\log _{a}(x)}$ 

• Лагарыфм кораня:

${\displaystyle \log _{a}{\sqrt[{p}]{x}}={\frac {\log _{a}(x)}{p}}}$ 

• Калі аснова лагарыфма ёсць ступень некаторага выразу:

${\displaystyle \log _{a^{k}}b={\frac {1}{k}}\log _{a}b.}$ 

Доказ: Гэта тоеснасць атрымліваецца адразу, калі ад лагарыфма па аснове ${\displaystyle a^{k}}$  перайсці да лагарыфма па аснове ${\displaystyle a}$ .

Вынікі:

• ${\displaystyle \log _{\sqrt[{n}]{a}}b=n\log _{a}b;}$ 
  ${\displaystyle \log _{a^{k}}{b^{p}}={\frac {p}{k}}\log _{a}{b};}$ 
  ${\displaystyle \log _{a^{k}}b^{k}=\log _{a}b.}$ 
• Яшчэ адна карысная тоеснасць:

${\displaystyle c^{\log _{a}b}=b^{\log _{a}c}}$ 

Доказ: Каб даказаць яе, заўважым, што лагарыфмы ў левай і правай частках супадаюць па аснове ${\displaystyle a}$ , а тады, згодна з вынікам з асноўнай лагарыфмічнай тоеснасці, левая і правая часткі тоесна роўныя.

Існуе відавочнае абагульненне прыведзеных формул:

${\displaystyle \log _{a}|xy|=\log _{a}|x|+\log _{a}|y|}$ 
${\displaystyle \log _{a}\left|{\frac {x}{y}}\right|=\log _{a}|x|-\log _{a}|y|}$ 

Формула для лагарыфма здабытку без цяжкасцей абагульняецца на адвольную колькасць сумножнікаў:

${\displaystyle \log _{a}(x_{1}x_{2}\dots x_{n})=\log _{a}(x_{1})+\log _{a}(x_{2})+\dots +\log _{a}(x_{n})}$ 

Апісанымі ўласцівасцямі і тлумачыцца, чаму выкарыстанне лагарыфмаў (да вынаходніцтва калькулятараў) істотна палягчала вылічэнні. Напрыклад, множанне шматзначных лікаў ${\displaystyle x,y}$  з дапамогай лагарыфмічных табліц адбывалася па наступнаму алгарытму:

1. Знайсці ў табліцах лагарыфмы лікаў ${\displaystyle x,y}$ .
2. Скласці гэтыя лагарыфмы, атрымаўшы такім чынам (згодна з первай уласцівасцю) лагарыфм здабытку ${\displaystyle x\cdot y}$ .
3. Па лагарыфму здабытку знайсці ў табліцах сам здабытак.

Дзяленне, якое без дапамогі лагарыфмаў істотна больш працаёмкае чым множанне, выконвалася па таму ж алгарытму, толькі з заменай складання лагарыфмаў на адыманне. Гэтак жа спрашчаліся ўзвядзенне ў ступень і здабыванне кораня.

Замена асновы лагарыфма

• Ад лагарыфма ${\displaystyle \log _{a}b}$  па аснове ${\displaystyle a}$  можна перайсці да лагарыфма па другой аснове ${\displaystyle c}$ :

${\displaystyle \log _{a}b={\frac {\log _{c}b}{\log _{c}a}}}$ 

• Вынік: перастаноўка асновы і лагарыфмуемага выразу:

${\displaystyle \log _{a}b={\frac {1}{\log _{b}a}}}$ 

Лагарыфмічная функцыя

 

 

 

 

Асноўныя уласцівасці

Калі разглядаць лагарыфмаваны лік як зменную, мы атрымаем лагарыфмічную функцыю ${\displaystyle y=\log _{a}x}$ . Яна вызначана пры ${\displaystyle a>0;\ a\neq 1;x>0}$ .

• Абсяг вызначэння: ${\displaystyle x>0}$ .
• Абсяг значэнняў: ${\displaystyle E(y)=(-\infty ;+\infty )}$ .

Гэта крывая часта называецца лагарыфмікай.

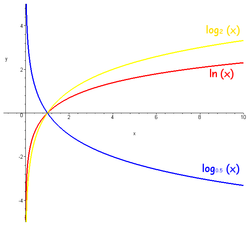
• З формулы замены асновы лагарыфма відаць, што графікі лагарыфмічных функцый з рознымі асновамі, большымі за адзінку, адрозніваюцца адзін ад аднаго толькі расцяжэннем уздоўж восі ${\displaystyle y}$ :

${\displaystyle \log _{b}x={\frac {\log _{a}x}{\log _{a}b}}}$ 

• Графікі для асноў ${\displaystyle a}$  і ${\displaystyle 1/a}$  сіметрычныя адносна восі x.
• З азначэння вынікае, што лагарыфмічная функцыя ${\displaystyle y=\log _{a}x}$  адваротная да паказнікавай функцыі ${\displaystyle y=a^{x}}$ , таму іх графікі сіметрычныя адносна бісектрысы першага і трэцяга квадрантаў (гл. рысунак). Як і паказнікавая, лагарыфмічная функцыя трансцэндэнтная.
• Лагарыфмічная функцыя строга нарастае пры ${\displaystyle a>1}$  (гл. графікі) і строга спадае пры ${\displaystyle 0$ . Графік любой лагарыфмічнай функцыі праходзіць праз кропку ${\displaystyle (1;0)}$ . Функцыя непарыўная і бесканечна дыферэнцавальная ўсюды на сваім абсягу вызначэння.
• Вось ардынат ${\displaystyle (x=0)}$  з’яўляецца вертыкальнаю асімптотай для лагарыфмічнай функцыі, бо:

${\displaystyle \lim _{x\to +0}\log _{a}x=-\infty }$  пры ${\displaystyle a>1;}$ 
${\displaystyle \lim _{x\to +0}\log _{a}x=+\infty }$  пры ${\displaystyle 0$ 

• Вытворная лагарыфмічнай функцыі:

${\displaystyle (\log _{a}x)'={\frac {1}{x\ln a}}}$ 

• Першаісная лагарыфмічнай функцыі:

${\displaystyle \int \log _{a}x\,dx=x\log _{a}x-{\frac {x}{\ln a}}+C,}$ 

дзе C — адвольная сталая.

• З пункту гледжання алгебры, лагарыфмічная функцыя ажыццяўляе (адзіны магчымы) ізамарфізм групы адносна множання дадатных рэчаісных лікаў і групы адносна складання ўсіх рэчаісных лікаў. Іншымі словамі, лагарыфмічная функцыя з’яўляецца адзіным (вызначаным для ўсіх дадатных значэнняў аргумента) непарыўным рашэннем функцыянальнага ўраўнення:

${\displaystyle f(xy)=f(x)+f(y).}$ 

Натуральны лагарыфм

Прыведзеная вышэй агульная формула вытворнай выглядае найпрасцей у выпадку натуральнага лагарыфма:

${\displaystyle {\frac {d}{dx}}\ln x={\frac {1}{x}}.}$ 

З гэтай прычыны ў матэматычных даследаваннях пераважна выкарыстоўваюць іменна натуральныя лагарыфмы. Яны нярэдка з’яўляюцца пры развязанні дыферэнцыяльных ураўненняў, даследаванні статыстычных залежнасцей (напрыклад, размеркавання простых лікаў) і пад.

 

Праінтэграваўшы формулу для вытворнай у прамежку ад ${\displaystyle x=1}$  да ${\displaystyle x=b}$ , атрымліваем:

${\displaystyle \ln b=\int \limits _{1}^{b}{\frac {dx}{x}}.}$ 

Інакш кажучы, натуральны лагарыфм роўны плошчы пад гіпербалай ${\displaystyle y={\frac {1}{x}}}$  на названым прамежку x.

Нявызначаны інтэграл ад натуральнага лагарыфма лёгка знайсці інтэграваннем па частках:

${\displaystyle \int {\ln x\,\mathrm {d} x}=x\ln x-x+C.}$ 

У матэматычным аналізе і тэорыі дыферэнцыяльных ураўненняў вялікую ролю адыгрывае паняцце лагарыфмічнай вытворнай функцыі ${\displaystyle f(x)}$ :

${\displaystyle {\frac {d}{dx}}\ln(f(x))={\frac {f'(x)}{f(x)}}.}$ 

Раскладанне ў рад і вылічэнне натуральнага лагарыфма

Раскладзём натуральны лагарыфм у рад Тэйлара каля адзінкі:

${\displaystyle \ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\dots .}$ 

Гэты рад збягаецца пры ${\displaystyle -1$  У прыватнасці:

${\displaystyle \ln 2=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+\dots .}$ 

Формула непрыдатная для практычнага вылічэння лагарыфмаў з-за таго, што рад збягаецца вельмі павольна і толькі на вузкім прамежку. Аднак нескладана атрымаць з яе зручнейшую формулу:

${\displaystyle \ln \left({\frac {1+x}{1-x}}\right)=2\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\dots \right).}$ 

Гэты рад збягаецца хутчэй, і акрамя таго, цяпер левая частка формулы можа прадставіць лагарыфм любога дадатнага ліку.

Карыстацца апошняй формулай трэба так. Няхай ${\displaystyle Z}$  — лік, лагарыфм якога трэба вылічыць.

1) З ураўнення

${\displaystyle Z={\frac {1+x}{1-x}}}$ 

знаходзім ${\displaystyle x}$ :

${\displaystyle x={\frac {Z-1}{Z+1}}.}$ 

2) Вылічанае значэнне ${\displaystyle x}$  падстаўляем у рад і атрымліваем значэнне ${\displaystyle \ln Z}$ .

Дадзены алгарытм ужо прыдатны да выкарыстання на практыцы пры вылічэнні значэнняў лагарыфмаў, аднак ён не найлепшы з пункту гледжання працаёмкасці. Існуюць больш дзейсныя алгарытмы.

Лімітавыя суадносіны

Прывядзём некалькі карысных лімітаў, якія ўтрымліваюць лагарыфмы.

${\displaystyle \lim _{x\to 0}{\frac {\log _{a}(1+x)}{x}}=\log _{a}e={\frac {1}{\ln a}}}$ 
${\displaystyle \lim _{x\to +0}x^{b}\log _{a}x=0\quad (b>0)}$ 
${\displaystyle \lim _{x\to +\infty }{\frac {\log _{a}x}{x^{b}}}=0\quad (b>0)}$ 
${\displaystyle \ln x=\lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)}$ 
${\displaystyle \ln x=\lim _{h\to 0}{\frac {x^{h}-1}{h}}}$ 

Іншыя ўласцівасці

• З тэарэмы Гельфонда вынікае, што калі ${\displaystyle a,b}$  — алгебраічныя лікі (${\displaystyle a\neq 1}$ ), то ${\displaystyle \log _{a}b}$  або рацыянальны, або трансцэндэнтны. Пры гэтым лагарыфм рацыянальны і роўны ${\displaystyle {\frac {p}{q}}}$  толькі ў тым выпадку, калі лікі ${\displaystyle a,b}$  суадносяцца як ${\displaystyle a^{p}=b^{q}}$ .

• Сума ${\displaystyle \sum _{k=1}^{n}{\frac {1}{k}}}$  (частковая сума гарманічнага рада) пры вялікіх ${\displaystyle n}$  паводзіць сябе як ${\displaystyle \ln n+C}$ , дзе ${\displaystyle C\approx 0{,}577215664\dots }$  — сталая Ойлера — Маскероні.

Вызначэнне і ўласцівасці

Для камплексных лікаў лагарыфм вызначаецца гэтак жа, як рэчаісны. На практыцы выкарыстоўваецца амаль выключна натуральны камплексны лагарыфм, які пазначаецца ${\displaystyle \mathrm {Ln} \,z}$  і вызначаецца як рашэнне ${\displaystyle w}$  ураўнення ${\displaystyle e^{w}=z}$  (іншыя, эквівалентныя дадзеным, варыянты вызначэння прыведзены ніжэй).

У полі камплексных лікаў рашэнне гэтага ўраўнення, у адрозненне ад рэчаіснага выпадку, не вызначана адназначна. Напрыклад, згодна з тоеснасцю Эйлера, ${\displaystyle ~e^{\pi i}=-1}$ ; аднак таксама ${\displaystyle ~e^{-\pi i}=e^{3\pi i}=e^{5\pi i}\dots =-1}$ . Гэта звязана з тым, што паказальная функцыя ўздоўж ўяўнай восі з’яўляецца перыядычнай (з перыядам ${\displaystyle ~2\pi }$ ), і адно і тое ж значэнне функцыя прымае бясконца шмат разоў. Такім чынам, комплексная лагарыфмічная функцыя ${\displaystyle ~w=\mathrm {Ln} \,z}$  з’яўляецца шматзначнай.

Камплексны нуль не мае лагарыфма, паколькі камплексная экспанента не прыймае нулявога значэння. Ненулявое ${\displaystyle z}$  можна прадставіць у паказальнай форме:

${\displaystyle z=r\cdot e^{i\varphi }}$ 

Тады ${\displaystyle \mathrm {Ln} \,z}$  знаходзіцца па формуле:

${\displaystyle \mathrm {Ln} \,z=\ln r+i\left(\varphi +2\pi k\right)}$ 

Тут ${\displaystyle \ln \,r=\ln \,|z|}$  — рэчаісны лагарыфм, ${\displaystyle k}$  — адвольны цэлы лік. Адсюль выцякае:

 

З формулы відаць, што ў аднаго і толькі аднаго са значэнняў уяўная частка знаходзіцца ў інтэрвале ${\displaystyle ~(-\pi ,\pi ]}$ . Гэта значэнне называецца галоўным значэннем комплекснага натуральнага лагарыфма. Адпаведная (ужо адназначная) функцыя называецца галоўнай галіной лагарыфма і пазначаецца ${\displaystyle \ln \,z}$ . Часам праз ${\displaystyle \ln \,z}$  таксама пазначаюць значэнне лагарыфма, якое ляжыць не на галоўнай галіне. Калі ${\displaystyle z}$  — рэчаісны лік, то галоўнае значэнне яго лагарыфма супадае з звычайным рэчаісным лагарыфмам.

З прыведзенай формулы таксама вынікае, што рэчаісная частка лагарыфма вызначаецца наступным чынам праз кампаненты аргумента:

${\displaystyle \operatorname {Re} (\ln(x+iy))={\frac {1}{2}}\ln(x^{2}+y^{2})}$ 

На малюнку паказана, што рэчаісная частка як функцыя кампанентаў цэнтральна-сіметрычна і залежыць толькі ад адлегласці да пачатку каардынатаў. Яна атрымліваецца кручэннем графіка рэчаіснага лагарыфма вакол вертыкальнай восі. З набліжэннем да нуля функцыя імкнецца да ${\displaystyle -\infty .}$ 

Прыклады значэнняў комплекснага лагарыфма

Прывядзем галоўнае значэнне лагарыфма (${\displaystyle \ln }$ ) і агульны яго выраз (${\displaystyle \mathrm {Ln} }$ ) для некаторых аргументаў:

${\displaystyle \ln(1)=0;\;\mathrm {Ln} (1)=2k\pi i}$ 
${\displaystyle \ln(-1)=i\pi ;\;\mathrm {Ln} (-1)=(2k+1)i\pi }$ 
${\displaystyle \ln(i)=i{\frac {\pi }{2}};\;\mathrm {Ln} (i)=i{\frac {4k+1}{2}}\pi }$ 

Варта быць асцярожным пры пераўтварэннях комплексных лагарыфмаў, прымаючы пад увагу, што яны шматзначныя, і таму з роўнасці лагарыфмаў якіх-небудзь выразаў не варта роўнасць гэтых выразаў. Прыклад памылковай развагі:

${\displaystyle i\pi =\ln(-1)=\ln((-i)^{2})=2\ln(-i)=2(-i\pi /2)=-i\pi }$  — відавочная памылка.

Адзначым, што злева варта галоўнае значэнне лагарыфма, а справа — значэнне з ніжэйшай галіны (${\displaystyle k=-1}$ ). Прычына памылкі — неасцярожнае выкарыстанне ўласцівасці ${\displaystyle \log _{a}{(b^{p})}=p~\log _{a}b}$ , якая, наогул кажучы, мае на ўвазе ў комплексным выпадку ўвесь бясконцы набор значэнняў лагарыфма, а не толькі галоўнае значэнне.

Камплексная лагарыфмічная функцыя і рыманавая паверхня

 

У камплексным аналізе замест разгляду мнагазначных функцый на камплекснай плоскасці прынята іншае рашэнне: разглядаць функцыю як адназначную, але вызначаную не на плоскасці, а на больш складанай разнастайнасці, якоая называецца рыманавай паверхняй. Камплексная лагарыфмічная функцыя таксама адносіцца да гэтай катэгорыі: яе вобраз складаецца з бясконцага ліку галін, закручаных ў выглядзе спіралі. Гэтая паверхню бесперапынная і аднасувязная. Адзіны нуль у функцыі (першага парадку) атрымліваецца пры ${\displaystyle z=1}$ . Асаблівыя пункты: ${\displaystyle z=0}$  і ${\displaystyle z=\infty }$  (пункты разгалінавання бясконцага парадку).

У сілу аднасувязнасці рыманавая паверхня лагарыфма з’яўляецца універсальнай накрываючай для камплекснай плоскасці без пункту ${\displaystyle 0}$ .

Аналітычны працяг

Лагарыфм камплекснага ліку таксама можа быць вызначаны як аналітычны працяг рэчаіснага лагарыфма на ўсю камплексную плоскасць. Хай крывая ${\displaystyle \Gamma }$  пачынаецца ў адзінцы, не праходзіць праз нуль і не перасякае адмоўную частку рэчаіснай восі. Тады галоўнае значэнне лагарыфма ў канчатковым пункце ${\displaystyle w}$  крывой ${\displaystyle \Gamma }$  можна вызначыць па формуле:

${\displaystyle \ln z=\int \limits _{\Gamma }{du \over u}}$ 

Калі ${\displaystyle \Gamma }$  — простая крывая (без самаперасячэнняў), то для лікаў, якія ляжаць на ёй, лагарыфмічныя тоеснасці можна ўжываць без боязі, напрыклад:

${\displaystyle \ln(wz)=\ln w+\ln z,~\forall z,w\in \Gamma \colon zw\in \Gamma }$ 

Галоўная галіна лагарыфмічнай функцыі бесперапынная і дыферэнцыруема на ўсёй камплекснай плоскасці, акрамя адмоўнай часткі рэчаіснай восі, на якой уяўная частка скокам мяняецца на ${\displaystyle 2\pi }$ . Але гэты факт ёсць следства штучнага абмежавання ўяўнай часткі галоўнага значэння інтэрвалам ${\displaystyle ~(-\pi ,\pi ]}$ . Калі разгледзець усе галіны функцыі, то бесперапыннасць мае месца ва ўсіх пунктах, акрамя нуля, дзе функцыя не вызначана. Калі дазволіць крывой ${\displaystyle \Gamma }$  перасякаць адмоўную частка рэчаіснай восі, то першае такое скрыжаванне пераносіць вынік з галіны галоўнага значэння на суседнюю галіну, а кожнае наступнае скрыжаванне выклікае аналагічнае зрушэнне па галінах лагарыфмічнай функцыі.

З формулы аналітычнага працягу вынікае, што на любой галіне лагарыфма:

${\displaystyle {\frac {d}{dz}}\ln z={1 \over z}}$ 

Для любой акружнасці ${\displaystyle S}$ , якая ахоплівае пункт ${\displaystyle 0}$ :

${\displaystyle \oint \limits _{S}{dz \over z}=2\pi i}$ 

Інтэграл бярэцца ў станоўчым напрамку (супраць гадзіннікавай стрэлкі). Гэта тоеснасць ляжыць у аснове тэорыі вылікаў.

Можна таксама вызначыць аналітычнае працяг комплекснага лагарыфма з дапамогай вышэйпрыведзеных радоў: раду 1 або раду 2, — абагульненых на выпадак камплекснага аргументу. Аднак з выгляду гэтых радоў вынікае, што ў адзінцы сума раду роўная нулю, шэта значыць рад адносіцца толькі да галоўнай галіны шматзначнай функцыі камплекснага лагарыфма. Радыус збежнасці абодвух радоў роўны 1.

Сувязь са зваротнымі трыганаметрычнымі і гіпербалічнымі функцыямі

Паколькі камплексныя трыганаметрычныя функцыі звязаныя з экспанентай (формула Эйлера), то камплексны лагарыфм як зваротная да экспаненты функцыя звязаны са зваротнымі трыганаметрычнымі функцыямі:

${\displaystyle \operatorname {Arcsin} z=-i\operatorname {Ln} (iz+{\sqrt {1-z^{2}}})}$ 
${\displaystyle \operatorname {Arccos} z=-i\operatorname {Ln} (z+i{\sqrt {1-z^{2}}})}$ 
${\displaystyle \operatorname {Arctg} z=-{\frac {i}{2}}\ln {\frac {1+zi}{1-zi}}+k\pi \;(z\neq \pm i)}$ 
${\displaystyle \operatorname {Arcctg} z=-{\frac {i}{2}}\ln {\frac {zi-1}{zi+1}}+k\pi \;(z\neq \pm i)}$ 

Гіпербалічныя функцыі на камплекснай плоскасці можна разглядаць як трыганаметрычныя функцыі ўяўнага аргументу, таму і тут мае месца сувязь з лагарыфмам:

${\displaystyle \operatorname {Arsh} z=\operatorname {Ln} (z+{\sqrt {z^{2}+1}})}$  — зваротны гіпербалічны сінус
${\displaystyle \operatorname {Arch} z=\operatorname {Ln} \left(z+{\sqrt {z^{2}-1}}\right)}$  — зваротны гіпербалічны косінус
${\displaystyle \operatorname {Arth} z={\frac {1}{2}}\operatorname {Ln} \left({\frac {1+z}{1-z}}\right)}$  — зваротны гіпербалічны тангенс
${\displaystyle \operatorname {Arcth} z={\frac {1}{2}}\operatorname {Ln} \left({\frac {z+1}{z-1}}\right)}$  — зваротны гіпербалічны катангенс

Табліцы лагарыфмаў

 

З уласцівасцей лагарыфма вынікае, што замест працаёмкага множання шматзначных лікаў дастаткова адшукаць (па табліцах) і скласці іхнія лагарыфмы, а потым па тых жа табліцах («Антылагарыфмы») выканаць ступеняванне, г.зн. знайсці значэнне па яго лагарыфму. Выкананне дзялення адрозніваецца толькі тым, што лагарыфмы адымаюцца.

Першыя табліцы лагарыфмаў выдаў Джон Непер (1614), і яны ўтрымівалі толькі лагарыфмы трыганаметрычных функцый, прычым з памылкамі. Незалежна ад яго свае табліцы надрукаваў Ёст Бюргі, друг Кеплера (1620). У 1617 годзе оксфардскі прафесар матэматыкі Генры Брыгс выдаў табліцы, якія ўжо ўключалі дзесятковыя лагарыфмы лікаў ад 1 да 1000, з 8 (пазней — з 14) знакамі. Але і ў табліцах Брыгса выявіліся памылкі. Першае безпамылковае выданне на аснове табліц Георга Вегі (1783) з’явілася толькі ў 1857 годзе ў Берліне (табліцы Брэмікера, Carl Bremiker).

У Расіі першыя табліцы лагарыфмаў былі выдадзены ў 1703 годзе пры ўдзеле Л. П. Магніцкага. У СССР было выдадзена некалькі зборнікаў табліц лагарыфмаў:

1. Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Табліцы Брадзіса, выдаваныя з 1921 года, выкарыстоўваліся ў навучальных установах і ў інжынерных разліках, якія не патрабавалі вялікай дакладнасці. Яны ўтрымлівалі мантысы дзесятковых лагарыфмаў і трыганаметрычных функцый, натуральныя лагарыфмы і некаторыя іншыя карысныя разліковыя прылады.
2. Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Адмысловы зборнік для дакладных вылічэнняў.
3. Бремикер К. Логарифмо-тригонометрические таблицы. М.: Наука, 1962. 664 с. Класічныя шасцізначныя табліцы, зручныя для разлікаў з трыганаметрычнымі функцыямі.
4. Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6-е издание, М.: Наука, 1972.
5. Таблицы натуральных логарифмов, 2-е издание, в 2 томах, М.: Наука, 1971.
6. Десятизначные таблицы логарифмов комплексных чисел. М., 1952.

Лагарыфмічная лінейка

У 1620-я гады Эдмунд Уінгейт і Уільям Оўтрэд вынайшлі першую лагарыфмічную лінейку, якая да з’яўлення кішэнных калькулятараў была незаменнай вылічальнай прыладай інжынера. З дапамогай гэтай невялічкай прылады можна было хутка выконваць усе алгебраічныя аперацыі, у тым ліку з трыганаметрычнымі функцыямі. Дакладнасць разлікаў — каля 3 значных лічб.

 

• Камплексны лік
• Паказнікавая функцыя
• Камплексны лагарыфм
• Ступеняванне
• Лагарыфмічная лінейка
• Сістэмы злічэння
• Спіс інтэгралаў ад лагарыфмічных функцый