Декартов Координатен Систем

Секоја линија е наречена „координатна оска“ или само „оска“, а точката во која се пресекуваат се нарекува „координатен почеток“, обично во подредениот пар (0,0). Координатите можат да се претстават и како положби на правоаголните проекции на точката врз двете оски, изразени како растојанија од почетокот.

На истиот начин може да се претстави и точка во тридимензионален простор, но со три координати, кои се означените растојанија на ри заемно нормални рамнини (или со правоаголната проекција брз три заемно нормални линии). Истото важи и за точка во било која димензија n, чија положба ја одредуваме користејќи n координати, кои се означени растојанија од n заемно нормални хиперрамнини.

Изумувањето на координатниот систем претставува епохален момент во математиката, кој за првпат овозможил методолошка врска помеѓу геометријата и алгебрата. Користејќи го овој систем можеме да претставуваме геометриски фигури (на пр. криви) како Декартови равенки, кои се алгебарски равенки со координати на точките што лежат на фигурата. На пример, една кружница со полупречник 2 може да се опише како множество од сите точки чиишто координати x и y ја задоволуваат равенката x² + y² = 4.

Декартовите координати се камен-темелник на аналитичката геометрија и даваат геометриски толкувања во многу други математички гранки како што е линеарната алгебра, комплексната анализа, диференцијалната геометрија, повеќепроменливата анализа, теоријата на групите и други. Познат пример за примена на системот е графикот на функција. Декартовите координати се незаменливи и во многу други применети полиња што работат со геметрија, како астрономијата, физиката, инженерството и многу други. Ова е најзастапениот координатен систем во изработката на сметачка графика, сметачки-потпомогнатото конструирање (CAD) и други обработки на податоци поврзани со геметријата, т.е. што користат пресметковна геометрија.

Творецот на овој систем е францускиот математичар и филозоф Рене Декарт (1596-1650). Идејата се развила во 1637 во две независни дела на Декарт и Пјер де Ферма. Ферма работел со три димензии, но не го објавил пронајдокот. Во делото „Геометрија“ (La Géométrie) Декарт поподробно ја образложува новата замисла како да се претстави положбата на една точка или предмет на некоја површина со помош на оски што се сечат и поделоци за мерење.

Декартовиот координатен систем го овозможил развојот на перспективната и проективната геометрија. Подоцна системот одиграл суштинска улога и во развојот на анализата, чии творци се Исак Њутн и Готфрид Вилхелм Лајбниц.

Оттогаш наваму се измислени разни други координатни системи како поларниот за рамнина и сферниот и цилиндричниот систем за тридимензионален простор.

Декартови координати во две димензии

Денешниот Декартов координатен систем во две димензии се сосоти од нормални линии (оски), една иста единица за двете оски и ориентација на секоја оска. Линиите се нарекуваат x-оска и y-оска, првата хоризонтална, а втората вертикална. Точката во која се среќаваат е заеднички почеток, па со тоа секоја оска е бројна оска. За некоја точка P, низ неа се повлекува линија нормална на x-оската за да ја пресече таа оска X и друга линија P нормална на y-оската за да се пресече со таа оска Y. Потоа координатите на точката P се X и Y протолкувани како броеви x и y на соодветните бројни оски. Координатите се запишуваат како подреден пар (x, y). Точката во која се сечат оските е заедничкиот почеток на двете бројни линии и се нарекува „координатен почеток“ и се означува со O, па во тој случај оските можат да се наречат и Ox и Oy. Рамнина со оски x и y се нарекува Декартова рамнина или „рамнина xy“. Вредноста на x се нарекува „координата x“ или апсциса, а вредноста на y се нарекува „координата y“ или ордината.

Декартови координати во три димензии

 

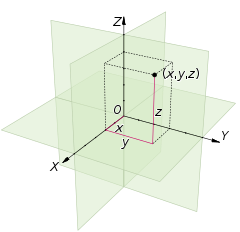
Декартовиот координатен систем во три димензии има три линии (оски) кои се заемно нормални, заедничка единица за должина и ориентација на секоја оска. Како и кај дводимензионалниот систем, секоја оска е бројна оска. Координатите на точката p се добиваат со повлекување на три линии низ p кои се нормални на секоја координатна оска, и запишување на местата кајшто линиите ќе се пресечат со оските како три броја.

Координатите на точката p можат да се претстават и како предозначени растојанија од p до трите рамнини што ги определуваат трите оски. Ако оските се наречени x, y и z, тогаш координатата x е растојанието од рамнината што ја определуваат оските y и z. Растојанието треба да е означено со предзнакот + или −, зависно од тоа во кој полупростор што го сече рамнината се наоѓа p. На истиот начин се добиваат и координатите y и z: првата од рамнината (x,z), а другата од рамнината (x,y).

 

Квадранти и октанти

 

Оските на дводимензионалниот Декартов систем ја делат рамнината на четири бесконечни дела наречени квадранти, секој ограничен со две полуоски. Квадрантите се означуваат со римски бројки и предзнак: I (+,+), II (−,+), III (−,−) и IV (+,−)

Тридимензионалниот Декартов систем ги дели просторот на октант, согласно предзнаците на координатите на точката. Октантот каде сите три координати се позитивни се нарекува прв октант, но не постои договорена номенклатура за останатите октанти. n-димензионалното воопштување на квадрантот и октантот се нарекува ортант.

Една рамнина со Декартов координатен систем се нарекува Декартова рамнина. Бидејќи координатите во овој систем се единствени и недвосмислени, точките на рамнината може да ги определуваат сите можни парови на реални броеви, т.е. со Декартовиот производ ${\displaystyle \mathbb {R} ^{2}=\mathbb {R} \times \mathbb {R} }$ , каде ${\displaystyle \mathbb {R} }$  е множеството на сите реални броеви. Така имаме и Декартов простор од било која димензија n, чии точки се „торки“ (набројувања) на n реални броеви, т.е. со ${\displaystyle \mathbb {R} ^{n}}$ .

Растојание помеѓу две точки

Растојанието помеѓу две точки на рамнината со Декартови координати ${\displaystyle (x_{1},y_{1})}$  и ${\displaystyle (x_{2},y_{2})}$  изнесува:

${\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}.}$ 

Ова е Декартовата варијанта на Питагорината теорема. Во тридимензионален простор, растојанието помеѓу точките ${\displaystyle (x_{1},y_{1},z_{1})}$  и ${\displaystyle (x_{2},y_{2},z_{2})}$  ќе биде

${\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}}}$ 

што може да се добие со две последователни примени на Питагорината теорема.

Формула за средишната точка

Средишната точка на отсечката која поврзува две точки во Декартовиот координатен систем се пресметува како просечна вредност на координатите на двете крајни точки на отсечката, а со помош на следнава формула:

${\displaystyle d={\frac {x_{2}+x_{1}}{2}},{\frac {y_{2}+y_{1}}{2}}.}$ 

Евклидови трансформации

Транслација

За да извршиме транслација на множество точки на рамнината, зачувувајќи ги нивните меѓурастојанија и насоки, додаваме еден ист пар броеви (X,Y) на координатите за секоја точка од множеството. Ако првичните координати на една точка се (x,y), по извршената транслација тие ќе бидат

${\displaystyle (x',y')=(x+X,y+Y).\,}$ 

Размерување

Ако сакаме да зголемиме или намалиме една фигура, ги помножуваме координатите на секоја точка со еден ист позитивен број m. Ако (x,y) се координатите на точка на првичната фигура, тогаш соодветната точка на разамерената фигура ќе ги има координатите

${\displaystyle (x',y')=(mx,my).\,}$ 

Ако m е поголем од 1, тогаш фигурата е поголема, а ако m е помеѓу 0 и 1, тогаш фигурата е помала.

Ротација

За да направиме ротација (свртување) на една фигура налево околу почетокот за извесен агол ${\displaystyle \theta }$ , тогаш ја заменуваме секоја точка со координати (x,y) со точка со координати (x',y'), каде

${\displaystyle x'=x\cos \theta -y\sin \theta \,}$ 
${\displaystyle y'=x\sin \theta +y\cos \theta .\,}$ 

Така: ${\displaystyle (x',y')=((x\cos \theta -y\sin \theta \,),(x\sin \theta +y\cos \theta \,)).}$ 

Отсликување

Ако (x, y) се координатите на една точка, тогаш (−x, y) се координатите на нејзината слика долж втората координатна оска (Y-оска), како линијата да е огледало. На истот начин, (x, −y) се координатите на сликата долж првата координатна оска (Х-оска).

Општи трансформаци

Трансформациите на рамнината се транслации, ротации, размерувања, отсликувања и нивни произволни композиции. Резултатот од ${\displaystyle (x',y')}$  примената на трансформација врз точката ${\displaystyle (x,y)}$  се добива со формулата

${\displaystyle (x',y')=(x,y)A+b\,}$ 

каде A е матрица 2×2, а b е пар од броеви кои зависат од трансформацијата; т.е.

${\displaystyle x'=xA_{11}+yA_{21}+b_{1}\,}$ 
${\displaystyle y'=xA_{12}+yA_{22}+b_{2}.\,}$ 

Матрицата A мора да има правоаголни редови со иста должина, т.е.

${\displaystyle A_{11}A_{21}+A_{12}A_{22}=0\,}$ 

и

${\displaystyle A_{11}^{2}+A_{12}^{2}=A_{21}^{2}+A_{22}^{2}.}$ 

Ова е исто што и A помножено со транспонираното мора да биде дијагонална матрица. Доколку овие услови не важат, тогаш формулата опишува поопшта афина трансформација на рамнината.

Формулите се однесуваат на транслација ако и само ако A е единична матрица. Трансформацијата е ротација околу некоја точка ако и само ако A е вртежна матрица, што значи дека

${\displaystyle A_{11}^{2}+A_{12}^{2}=A_{21}^{2}+A_{22}^{2}=A_{11}A_{22}-A_{21}A_{12}=1.}$ 

• Бројна оска
• Декартов производ
• Координатен систем
• Географски координатен систем