বীজগণিত: গণিতের শাখা
বীজগণিত (নামটি এসেছে আরবি: الجبر আল-জাবর থেকে, যার অর্থ ভাঙ্গা অংশসমূূহের পুনর্মিলন এবং হাড়সংযুক্তকরণ) গণিতের সংখ্যাতত্ত্ব, জ্যামিতি এবং গাণিতিক বিশ্লেষণের একটি বিস্তৃত ক্ষেত্র। অতি সাধারণ রূপে বীজগণিত হলো গাণিতিক চিহ্নগুলির অধ্যয়ন এবং এই চিহ্নগুলো নিপূণভাবে ব্যবহার করার নিয়ম; এটি গণিতের প্রায় সমস্ত শাখার সেতুবন্ধন স্বরূপ। এতে প্রাথমিক সমীকরণ সমাধান থেকে শুরু করে গ্রুপ, রিং এবং ক্ষেত্রগুলির মতো বিমূর্ত বিষয়সমূহের অধ্যয়ন পর্যন্ত সমস্ত কিছুই অন্তর্ভুক্ত রয়েছে। বীজগণিতের মৌলিক অংশগুলিকে প্রাথমিক বীজগণিত বলা হয়ে থাকে এবং বিমূর্ত অংশগুলিকে বিমূর্ত বীজগণিত বা আধুনিক বীজগণিত বলা হয়। প্রাথমিক বীজগণিতকে সাধারণত গণিত, বিজ্ঞান বা প্রকৌশল বিষয়ক অধ্যয়নের জন্য; এমনকি ঔষধ, অর্থনীতি সম্পর্কিত প্রয়োগের জন্যও অপরিহার্য বলে মনে করা হয়ে থাকে। বিমূর্ত বীজগণিত হল উন্নত গণিতের একটি প্রধান ক্ষেত্র, যা মূলত পেশাদার গণিতবিদরা অধ্যয়ন করে থাকে।
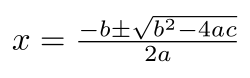
প্রাথমিক বীজগণিতের বিমূর্ত ব্যবহার পাটীগণিত থেকে পৃথক, যেমনঃ বীজগণিতে অজানা সংখ্যার মান নির্ণয়ের জন্য যে অক্ষর ব্যবহার করা হয়ে থাকে, তা একাধিক মান গ্রহণ করতে পারে। উদাহরণস্বরূপ, তে অক্ষরটি অজানা, তবে যোগাত্মক বিপরীত সংখ্যার ধারণা প্রয়োগের মাধ্যমে এর মান নির্ণয় করা যেতে পারে: । E = mc2 তে, এবং অক্ষরসমূহ চলক এবং অক্ষর একটি ধ্রুবক, যা শূন্যে আলোর গতি নির্দেশ করে। বীজগণিতে সূত্র লেখার এবং সমীকরণগুলি সমাধান করার জন্য অনেক পদ্ধতি রয়েছে, যা কথায় সমস্ত কিছু লেখার পুরনো পদ্ধতির চেয়ে অনেক বেশি স্পষ্ট এবং সহজ।
বীজগণিত শব্দটি নির্দিষ্ট কিছু বিশেষ পদ্ধতিতেও ব্যবহৃত হয়। বিমূর্ত বীজগণিতের একটি বিশেষ ধরনের গাণিতিক বস্তুকে "বীজগণিত" বলা হয় এবং শব্দটি ব্যবহৃত হয়। উদাহরণস্বরূপ, রৈখিক বীজগণিত, বীজগাণিতিক টপোলজি ইত্যাদি বীজগাণিতিক শাখাসমূহের নামে।
একজন গণিতবিদ যিনি বীজগণিতে গবেষণা করেন, তাকে বীজগণিতবিদ বলা হয়।বহু বীজগণিতবিদ মিলে এই বীজগণিতকে আরও অনেক সমৃদ্ধ করেছেন।যেমন,"রেনে দেকারতে"সেরকমই একজন বীজগণিতবিদ।
ব্যুৎপত্তি

বীজগণিত আরবি الجبر ("আল-জাবর" অর্থ "ভাঙা জিনিস পুনঃগঠিত করা") শব্দ থেকে এসেছে এবং শব্দটি ফার্সি গণিতবিদ এবং জ্যোতির্বিজ্ঞানী আল খারিজমি রচিত নবম শতাব্দীর প্রথম দিকের বই ইলমুল জাবর ওয়াল মুকাবালাহ্ ("পুনর্গঠন এবং ভারসাম্যের বিজ্ঞান") শিরোনাম থেকে এসেছে। আল-জাবর শব্দটি দিয়ে তার রচনায় তিনি সমীকরণের এক দিক থেকে পদ অন্য দিকে নিয়ে যাওয়ার পদক্ষেপকে বুঝিয়েছিলেন, المقابلة (আল-মুকাবালাহ্, অর্থগ "ভারসাম্য") দ্বারা উভয় পক্ষে সমান পদ যুক্ত করার বিষয়টিকে তিনি বুঝিয়েছিলেন। লাতিন ভাষায় আলজেবার অথবা আলজেবরা নামে সংক্ষিপ্ত হয়ে, অবশেষে পঞ্চদশ শতাব্দীতে স্পেনীয়, ইতালীয় বা মধ্যযুগীয় লাতিন ভাষা হয়ে ইংরেজি ভাষায় প্রবেশ করে। এটি প্রকৃতপক্ষে, ভাঙা বা স্থানচ্যুত হাড় স্থাপনের শল্য চিকিৎসার পদ্ধতিকে বোঝায়। গাণিতিক অর্থ (ইংরেজিতে) ষোড়শ শতাব্দীতে প্রথম নথিভূক্ত করা হয়েছিল।
বীজগণিত শব্দের বিভিন্ন অর্থ
"বীজগণিত" এর একক শব্দ বা পরিবর্ধকবাচক শব্দসহ গণিতে বেশ কয়েকটি সম্পর্কিত অর্থ রয়েছে।
- কোনও পদাশ্রিত নির্দেশক (article) ব্যতীত, একক শব্দ হিসেবে "বীজগণিত" গণিতের একটি বিস্তৃত অংশের নাম।
- একটি পদাশ্রিত নির্দেশক বা বহুবচনসহ একক শব্দ হিসেবে, "একটি বীজগণিত" বা "বীজগণিত" একটি নির্দিষ্ট গাণিতিক কাঠামো বোঝায়, যার সুনির্দিষ্ট সংজ্ঞা প্রসঙ্গের উপর নির্ভর করে। সাধারণত, কাঠামোর একটি যোগ, গুণ এবং স্কেলার গুণ রয়েছে (একটি ক্ষেত্রের উপরে বীজগণিত দেখুন)। কিছু লেখক যখন "বীজগণিত" শব্দটি ব্যবহার করেন, তখন তারা নিম্নলিখিতঃ সংযোজন, বিনিময়,অভেদক , এবং / অথবা, সসীম-মাত্রার অতিরিক্ত অনুমানের একটি উপসেট ব্যবহার করে থাকেন। সর্বজনীন বীজগণিতে, "বীজগণিত" শব্দটি উপরের ধারণার একটি সাধারণীকরণকে বোঝায়, যা এন-অ্যারি ক্রিয়াকলাপের অনুমতি দিয়ে থাকে।
- একটি পরিবর্ধকবাচক শব্দসহ, এখানে একই ধরনের পার্থক্য দেখা যায়:
- পদাশ্রিত নির্দেশক ব্যতীত নামটি বীজগণিতের একটি অংশকে বোঝায়, যেমনঃ রৈখিক বীজগণিত, প্রাথমিক বীজগণিত (প্রতীক-নিপুণভাবে ব্যবহার বিধি গণিতের প্রাথমিক কোর্সে প্রাথমিক ও মাধ্যমিক শিক্ষার অংশ হিসাবে শেখানো হয়), বা বিমূর্ত বীজগণিত (বিমূর্ত বীজগণিত অধ্যয়নকারীদের জন্য)।
- একটি পদাশ্রিত নির্দেশকসহ এর দ্বারা উদাহরণস্বরূপঃ কিছুটা বিমূর্ত কাঠামোকে বোঝায়, যেমনঃ একটি লাই বীজগণিত, একটি সহযোগী বীজগণিত, বা একটি শীর্ষ অপারেটর বীজগণিত।
- কখনও কখনও উভয় অর্থ একই যোগ্যতার জন্য উপস্থিত থাকে। যেমনঃ এক বাক্যে: বিনিময় বীজগণিত হল বিনিময় রিংগুলির অধ্যয়ন, যা পূর্ণসংখ্যার উপর বিনিময় বীজগণিত।
গণিতের একটি শাখা হিসেবে "বীজগণিত"
বীজগণিত পাটিগণিতের মতো হিসাব-নিকাশ দিয়ে শুরু হয়েছিল, যেখানে অক্ষর সংখ্যার মান ধারণ করতে পারে। যা যেকোন সংখ্যার জন্য ধর্মসমূহের প্রমাণ করতে সাহায্য করে।




ঐতিহাসিকভাবে এবং বর্তমান শিক্ষা ব্যবস্থায় বীজগণিতের অধ্যয়ন উপরের দ্বিঘাত সমীকরণের মতো সমীকরণের সমাধানের মাধ্যমে শুরু হয়। তারপরে আরও সাধারণ প্রশ্ন যেমন "একটি সমীকরণের সমাধান আছে কি?", "একটি সমীকরণের কতগুলি সমাধান আছে?", "সমাধানগুলির প্রকৃতি সম্পর্কে কী বলা যেতে পারে?" বিবেচনা করা হয়ে থাকে। এই প্রশ্নগুলো পরবর্তীতে বীজগণিতকে বিভিন্ন অ-সংখ্যাসূচক বিষয়সমূহ যেমনঃ বিন্যাস, ভেক্টর, ম্যাট্রিক্স এবং বহুপদী তে ব্যাপ্ত করে। এই অ-সংখ্যাসূচক বিষয়সমূহের কাঠামোগত বৈশিষ্ট্যগুলি তখন গ্রুপ, রিং এবং ক্ষেত্রের মতো বীজগণিতক কাঠামোতে বিমূর্ত হয়।
ষোড়শ শতাব্দীর আগে, গণিত কেবল দুটি উপ-ক্ষেত্র, পাটিগণিত এবং জ্যামিতিতে বিভক্ত ছিল। যদিও কিছু কিছু পদ্ধতি, যা অনেক আগে বিকশিত হয়েছিল, যা আজকাল বীজগণিত হিসাবে গণ্য করা যেতে পারে, বীজগণিতের উত্থান এবং এরপরেই কেবল ১৬শ বা ১৭শ শতকের দিকে অগণিত ক্যালকুলাস গণিতের শাখা হিসাবে আবির্ভূত হয় । উনিশ শতকের দ্বিতীয়ার্ধ থেকে, গণিতের অনেকগুলি নতুন ক্ষেত্র আবির্ভূত হয়েছিল, যার বেশিরভাগই পাটিগণিত এবং জ্যামিতি উভয়ই ব্যবহার করেছিল এবং প্রায় সবগুলিই বীজগণিত ব্যবহার করেছিল।
আজ, বীজগণিত বৃদ্ধি পেয়েছে যতক্ষণ না এতে গণিতের অনেকগুলি শাখা অন্তর্ভুক্ত হয়েছে , যেমনটি গণিতের বিষয় শ্রেণীবদ্ধকরণে দেখা যায়। যেখানে প্রথম স্তরের কোন অংশকে (দুটি অঙ্কের সংখ্যা) বীজগণিত বলা হতো না। আজ বীজগণিতের মধ্যে রয়েছে, ০৮-সাধারণ বীজগাণিতিক প্রক্রিয়া , ১২- ক্ষেত্র তত্ত্ব এবং বহুপদী, ১৩- বিনিময় বীজগণিত, ১৫- রৈখিক এবং বহুরেখা বীজগণিত ; ম্যাট্রিক্স তত্ত্ব, ১৬- সংযোজন রিং এবং বীজগণিত , ১৭- অসংযোজন রিং এবং বীজগণিত, ১৮- শ্রেণী তত্ত্ব ; সমসংস্থানিক বীজগণিত, ১৯- কে-তত্ত্ব এবং ২০- গ্রুপ তত্ত্ব । ১১- সংখ্যা তত্ত্ব এবং ১৪- বীজগাণিতিক জ্যামিতিতে বীজগণিত ব্যাপকভাবে ব্যবহৃত হয়।
ইতিহাস
বীজগণিতের আদি ইতিহাস

বীজগণিতের উৎপত্তি প্রাচীন ব্যাবিলনীয়দের কাছে শনাক্ত করা যায়, যারা একটি উন্নত পাটিগণিত ব্যবস্থা তৈরি করেছিল, যার সাহায্যে তারা একটি অ্যালগরিদমিক প্রক্রিয়ায় গণনা করতে সক্ষম হয়েছিল। ব্যাবিলনীয়রা রৈখিক সমীকরণ, দ্বিঘাত সমীকরণ এবং অনির্দিষ্ট রৈখিক সমীকরণ ব্যবহার করে বর্তমানে সমাধান করা সমস্যাগুলির সমাধান করার জন্য সূত্র তৈরি করেছিল। বিপরীতে, এই যুগের বেশিরভাগ মিশরীয়রা, পাশাপাশি গ্রীক ও চীনা গণিতও খ্রিস্টপূর্ব ১ম সহস্রাব্দে, সাধারণত জ্যামিতিক পদ্ধতি দ্বারা সমীকরণগুলি সমাধান করেছিল। যেমন রিহিন্দ ম্যাথমেটিক্যাল পাপিরাস, ইউক্লিডের উপাদানসমূহ এবং দ্য ম্যাথমেটিকাল আর্টস এর নবম অধ্যায়ে যার উল্লেখ পাওয়া যায় । গ্রীকদের জ্যামিতিক কাজ সূত্রকে সাধারণীকরণের জন্য নির্দিষ্ট সূত্রকে আরও সাধারণ পদ্ধতিতে উল্লেখকরণ ও সমীকরণের সমাধানের বাইরে সূত্রকে সাধারণীকরণের কাঠামো সরবরাহ করেছিল, যদিও মধ্যযুগীয় ইসলামে গণিতের বিকাশ না হওয়া পর্যন্ত এটি উপলব্ধি করা সম্ভব হয়নি।
প্লেটোর সময়কালে গ্রিক গণিতের ক্ষেত্রে এক বিরাট পরিবর্তন ঘটে গেছে । গ্রীকরা একটি জ্যামিতিক বীজগণিত তৈরি করেছিল যেখানে পদগুলি জ্যামিতিক বস্তুর পক্ষ দ্বারা প্রতিনিধিত্ব করা হতো, সাধারণত রেখা যেগুলির সাথে অক্ষর যুক্ত ছিল। দাওফান্তাস (খ্রিস্টীয় তৃতীয় শতাব্দী) ছিলেন আলেকজান্দ্রীয় গ্রিক গণিতবিদ এবং অ্যারিথমেটিকা নামে একাধিক বইয়ের লেখক। এই গ্রন্থগুলি বীজগাণিতিক সমীকরণগুলি সমাধান করার বিষয়ে আলোচনা করে, এবং সংখ্যা তত্ত্বকে ডায়োফান্তাইন সমীকরণের আধুনিক ধারণার দিকে নিয়ে গেছে।
উপরে আলোচিত পূর্ববর্তী ঐতিহ্যসমূহ ফার্সি গণিতবিদ মুহম্মদ ইবনে মুসা আল-খোয়ারিজমি (সি. ৭৮০-৮৫০) -এর উপর প্রত্যক্ষ প্রভাব ফেলেছিল। পরবর্তীতে, তিনি কমপ্লেশিয়াস বুক অন ক্যালকুলেশন বাই কমপ্লেশন অ্যান্ড ব্যালান্সিং লিখেছিলেন, যা বীজগণিতকে একটি গাণিতিক নিয়ম হিসাবে প্রতিষ্ঠিত করে;যা জ্যামিতি এবং পাটিগণিত থেকে স্বতন্ত্র।
হেলেনিস্টিক গণিতবিদ আলেকজান্দ্রিয়ার নায়ক এবং ডিওফ্যান্টাসের গণিতবিদগণ পাশাপাশি ব্রহ্মগুপ্তের মতো ভারতীয় গণিতবিদরা মিশর এবং ব্যাবিলনের ঐতিহ্য অব্যাহত রেখেছিলেন, যদিও ডিওফ্যান্টাসের অ্যারিথমেটিকা এবং ব্রহ্মগুপ্তের ব্রহ্মস্ফুটসিদ্ধান্ত উচ্চ স্তরে রয়েছে। উদাহরণস্বরূপ,৬২৮ খ্রিস্টাব্দে দ্বিঘাত সমীকরণের জন্য শূন্য ও ঋণাত্মক সমাধানসহ শব্দের মাধ্যমে প্রথম সম্পূর্ণ গাণিতিক সমাধানটি ব্রহ্মগুপ্ত তাঁর "ব্রহ্মসুফাসিদ্ধন্ত" গ্রন্থে বর্ণনা করেছিলেন। পরবর্তীতে,ফার্সি ও আরবি গণিতবিদগণ বীজগণিত পদ্ধতিগুলি কঠোর পরিশ্রমের মাধ্যমে উন্নত করেছিলেন। যদিও ডিওফান্টাস এবং ব্যাবিলনীয়রা সমীকরণগুলি সমাধানের জন্য বেশিরভাগ বিশেষ অ্যাডহক পদ্ধতি ব্যবহার করেছিল, আল-খয়ারিজমির অবদানটি ছিল মৌলিক। তিনি বীজগাণিতিক প্রতীক, ঋণাত্মক সংখ্যা বা শূন্য ছাড়াই রৈখিক এবং দ্বিঘাত সমীকরণগুলি সমাধান করেছিলেন, সুতরাং তাকে বিভিন্ন ধরনের সমীকরণকে আলাদা করতে হয়েছিল।
যেখানে বীজগণিতকে সমীকরণ তত্ত্বের সাথে সম্পৃক্ত করা হয়েছে,সেখানে গ্রিক গণিতবিদ ডিওফ্যান্টাস ঐতিহ্যগতভাবে "বীজগণিতের জনক" হিসাবে পরিচিতি পেয়েছেন এবং যেখানে সমীকরণগুলি পরিচালনা ও সমাধানের নিয়মগুলির সাথে সম্পৃক্ত , সেখানে ফার্সি গণিতবিদ আল-খোয়ারিজমিকে "বীজগণিতের জনক" হিসাবে বিবেচনা করা হয় । কে (সাধারণ অর্থে) "বীজগণিতের জনক" হিসাবে পরিচিত হওয়ার অধিক অধিকারপ্রাপ্ত তা নিয়ে এখন বিতর্ক রয়েছে। আল-জাবরের মধ্যে পাওয়া বীজগণিতটি অ্যারিথমেটিকাতে পাওয়া বীজগণিতের তুলনায় কিছুটা বেশি প্রাথমিক এবং অ্যারিথমেটিকা বাকবিতণ্ডিত, যেখানে আল-জাবর সম্পূর্ণরূপে আলংকারিক । যারা আল-খুয়ারিজমিকে সমর্থন করেন তারা এই বিষয়টির দিকে ইঙ্গিত করেন যে তিনি " পক্ষান্তর " এবং "ভারসাম্য"র পদ্ধতিগুলি চালু করেছিলেন (সমীকরণের এক দিক থেকে অন্য দিকে পদের স্থানান্তর, অর্থাৎ, সমীকরণ এর বিপরীত দিকে একই পদের বাতিলকরণ) যা 'আল-জাবর' শব্দটি দ্বারা মূলত বোঝানো হয়েছে, এবং তিনি দ্বিঘাত সমীকরণগুলি সমাধান করার একটি বিস্তৃত ব্যাখ্যা দিয়েছেন, এছাড়া তাঁর বীজগণিত আর মাথাব্যথার কারণ ছিল না " সমস্যার একটি সিরিজ পুনঃমীমাংসা করার সাথে , কিন্তু একটি বর্ণনামূলক বর্ণনা যা আদি পদের সমন্বয়ে গঠিত হয়,যেখানে সকল বিন্যাস সমীকরণ গঠনের জন্য সকল নিয়ম কানুন অবশ্যই দিবে,যা অতঃপর স্পষ্টভাবে অধ্যয়নের সত্য বস্তু গঠন করে"। তিনি একটি সমীকরণের স্বার্থে সমীকরণটি অধ্যয়নও করেছিলেন এবং "সাধারণ পদ্ধতিতে, কারণ এটি কোনও সমস্যার সমাধান করার ক্ষেত্রে কেবল উত্থিত হয় না, তবে এটি একটি অসীম শ্রেণীর সমস্যার সংজ্ঞা দেওয়ার জন্য বিশেষভাবে কাজে আসে"।
অপর ফার্সি গণিতবিদ ওমর খৈয়ামকে বীজগাণিতিক জ্যামিতির ভিত্তি শনাক্ত করার জন্য সম্মানিত করা হয় এবং তিনি ঘন সমীকরণের সাধারণ জ্যামিতিক সমাধান আবিষ্কার করেছিলেন।তাঁর গ্রন্থ ট্রিটাইজ অন ডেমোনস্টেশনস অফ প্রবলেমস অফ অ্যালজেবরা (১০৭০)এ বীজগণিতের নীতিমালা রচনা করেন, যা ফার্সি গণিতের অংশ যা শেষ পর্যন্ত ইউরোপে স্থানান্তরিত হয়েছিল। তবুও আরেক ফার্সি গণিতবিদ শারাফ আল দিন আল তুসি ঘন সমীকরণের বিভিন্ন ক্ষেত্রে বীজগাণিতিক এবং সংখ্যাসূচক সমাধান খুঁজে পেয়েছিলেন । তিনি একটি ফাংশনের ধারণাও বিকাশ করেছিলেন।ভারতীয় গণিতবিদ মহাবীর এবং দ্বিতীয় ভাস্কর ফারসি গণিতবিদ আল-কারাজি, এবং চীনা গণিতবিদ চু শি-চিয়ে, ঘনের বিভিন্ন ঘটনা সমাধান , দ্বিঘাত সমীকরণ, কুইন্টিক এবং উচ্চতর-পর্যায়ের বহুপদী সমীকরণ সমাধানের জন্য সংখ্যাগত একটা পদ্ধতি ব্যবহার করেন।১৩তম শতকে, একটি ঘন সমীকরণ গণিতবিদ ফিবোনাচ্চি দ্বারা সমাধান ইউরোপীয় বীজগণিতে রেনেসাঁ শুরুর একটি প্রতিনিধি। আবু আল-আসান ইবন আলি-আল-কালাসাদি (১৪১২-১৪৮৬) "বীজগণিতে প্রতীকবাদের প্রবর্তনের দিকে প্রথম পদক্ষেপ গ্রহণ করেছিলেন"।তিনি ∑ n 2, ∑ n 3 গণনা করেছিলেন এবং বর্গমূল নির্ধারণের জন্য ক্রমাগত আনুমানিক পদ্ধতিটি ব্যবহার করেছিলেন।
বীজগণিতের আধুনিক ইতিহাস

১৬শ শতাব্দীর শেষের দিকে নতুন বীজগণিত নিয়ে ফ্রান্সোইস ভিয়েটের কাজ আধুনিক বীজগণিতের দিকে গুরুত্বপূর্ণ পদক্ষেপ ছিল। ১৬৩৭ সালে, র্যনে দেকার্ত স্থানাঙ্ক জ্যামিতি আবিষ্কার করেন এবং আধুনিক বীজগাণিতিক চিহ্ন প্রবর্তন করে লা জিওম্যাট্রি প্রকাশ করেছিলেন।বীজগণিতের আরও বিকাশের আরেকটি মূল ঘটনা হল ঘন এবং দ্বিঘাত সমীকরণগুলির সাধারণ বীজগাণিতিক সমাধান,যা ১৬তম শতাব্দীর মাঝামাঝি সময়ে বিকশিত হয়েছিল।নির্ণায়কের ধারণাটি ১৭তম শতাব্দীতে জাপানি গণিতবিদ সেকি কোওয়া বিকাশ করেছিলেন এবং ম্যাট্রিক্স ব্যবহার করে এক সাথে রৈখিক সমীকরণের সিস্টেমগুলি সমাধানের উদ্দেশ্যে দশ বছর পরে গটফ্রাইড লাইবনিজ স্বাধীনভাবে তার অনুসরণ করেছিলেন। জোসেফ-লুই ল্যাঞ্জরেজ বিন্যাস অধ্যয়ন করেছিলেন,তিনি তার ১৭৭০-এর গবেষণাপত্র " রেফ্লেকশনস সুর লা রিসুলিউশন অ্যালজেব্রিক ডেস অ্যাকুয়েশনস "বাংলায় "বীজগাণিতিক সমীকরণ সমাধানের জন্য নিবেদিত" যেখানে তিনি ল্যাঞ্জরেজ রেসলভেন্টস প্রবর্তন করেছিলেন।পাওলো রুফিনি প্রথম ব্যক্তি ছিলেন যিনি বিন্যাসের গ্রুপ তত্ত্বটি বিকাশ করেছিলেন এবং তাঁর পূর্বসূরীদের মতো বীজগণিত সমীকরণ সমাধানের প্রসঙ্গেও তিনি অবদান রেখেছিলেন।
সমীকরণ সমাধানে আগ্রহ , প্রাথমিকভাবে গ্যালোয়া তত্ত্ব এবং গঠনমূলক বিষয়ের উপর দৃষ্টি নিবদ্ধ করার কারণে ১৯তম শতাব্দীতে বিমূর্ত বীজগণিত উন্নতি সাধন করেছিল। জর্জ পিইকক্ গণিত এবং বীজগণিত মধ্যে অচলিত চিন্তাধারা প্রতিষ্ঠাতা করেছিলেন। অগাস্টাস ডি মরগান তার প্রস্তাবিত যুক্তির সিস্টেমে রিলেশনাল বীজগণিত আবিষ্কার করেছিলেন। জোসিয়াহ উইলার্ড গিবস ত্রি-মাত্রিক স্থানের ভেক্টরগুলির একটি বীজগণিত বিকাশ করেছিলেন এবং আর্থার কেলি ম্যাট্রিক্সের একটি বীজগণিত বিকাশ করেছিলেন (এটি একটি অনিয়মিত বীজগণিত)।
বীজগণিত শব্দটিসহ গণিতের ক্ষেত্রসমূহ
গণিতের কিছু ক্ষেত্র যা বিমূর্ত বীজগণিতের শ্রেণিবিন্যাসের আওতায় আসে তাদের নামে বীজগণিত শব্দটি রয়েছে; রৈখিক বীজগণিত এর একটি উদাহরণ। অন্যদের নামে অবশ্য বীজগণিত শব্দটি নেই : গ্রুপ তত্ত্ব, রিং তত্ত্ব এবং ক্ষেত্র তত্ত্ব তার উদাহরণ। এই বিভাগে, আমরা গণিতের কিছু ক্ষেত্র তালিকাভুক্ত করেছি যাদের নামের সাথে "বীজগণিত" শব্দটি রয়েছে ।
- প্রাথমিক বীজগণিত, বীজগণিতের অংশ যা সাধারণত গণিতের প্রাথমিক পাঠ্যক্রমগুলিতে শেখানো হয়।
- বিমূর্ত বীজগণিত, যার মধ্যে গ্রুপ, রিং এবং ক্ষেত্রের মতো বীজগণিত কাঠামো স্বতঃসিদ্ধ ব্যবস্থায় সংজ্ঞায়িত এবং গবেষণা করা হয়।
- রৈখিক বীজগণিত, যেখানে রৈখিক সমীকরণের সুনির্দিষ্ট বৈশিষ্ট্য, ভেক্টর স্পেস এবং ম্যাট্রিক্স অধ্যয়ন করা হয়।
- বুলিয়ান বীজগণিত, বীজগণিত একটি শাখা সত্য মান মিথ্যা এবং সত্য এর দ্বারা সংক্ষিপ্ত হিসাব করে ।
- বিনিময় বীজগণিত, বিনিময় রিংগুলির অধ্যয়ন।
- কম্পিউটার বীজগণিত , অ্যালগরিদম এবং কম্পিউটার প্রোগ্রাম হিসাবে বীজগাণিতিক পদ্ধতিসমূহের প্রয়োগ।
- হোমোলজিকাল বীজগণিত, বীজগণিত কাঠামোর অধ্যয়ন যা টপোলজিকাল স্পেসগুলি অধ্যয়নের জন্য মৌলিক।
- সর্বজনীন বীজগণিত, যেখানে সমস্ত বীজগণিত কাঠামোর সাধারণ বৈশিষ্ট্য অধ্যয়ন করা হয়।
- বীজগণিত সংখ্যা তত্ত্ব, যেখানে সংখ্যার বৈশিষ্ট্যগুলি বীজগাণিতিক দৃষ্টিকোণ থেকে অধ্যয়ন করা হয়।
- বীজগাণিতিক জ্যামিতি, জ্যামিতির একটি শাখা, এর আদি আকারে বক্ররেখা এবং পৃষ্ঠতলকে বীজগাণিতিক সমীকরণের সমাধানের সাথে সম্পৃক্ত করে।
- বীজগণিত সম্মিলন, যেখানে সংযুক্তি প্রশ্নগুলি অধ্যয়নের জন্য বীজগণিত পদ্ধতি ব্যবহার করা হয়।
- রিলেশনাল বীজগণিত : অন্বয়ের একটি সেট যা নির্দিষ্ট অপারেটরের অধীনে বন্ধ থাকে
অনেক গাণিতিক কাঠামোকে বীজগণিত বলা হয়:
- একটি ক্ষেত্রের উপরে বীজগণিত বা আরও সাধারণতভাবে একটি রিংয়ের উপরে বীজগণিত
- ক্ষেত্র বা রিংয়ের মধ্যে বীজগণিতগুলির অনেক শ্রেণীর একটি নির্দিষ্ট নাম থাকে:
- সহযোগী বীজগণিত
- অ-সহযোগী বীজগণিত
- মিথ্যা বীজগণিত
- হফ বীজগণিত
- সি * -বীজগণিত
- প্রতিসম বীজগণিত
- বাহ্যিক বীজগণিত
- টেনসর বীজগণিত
- পরিমাপ তত্ত্ব ,
- বিভাগ তত্ত্বে
- এফ-বীজগণিত এবং এফ-সহযোগী বীজগণিত
- টি-বীজগণিত
- যুক্তিবিদ্যায় ,
- রিলেশন বীজগণিত, একটি অবশিষ্ট বুলিয়ান বীজগণিত যেটি কনভার্স নামে পরিচিতি লাভ করে প্রসারিত হয়েছিল।
- বুলিয়ান বীজগণিত, একটি পরিপূরক বিতরণ কাঠামো
- হেইটিং বীজগণিত
প্রাথমিক বীজগণিত

1 – ঘাত (সূচক)
2 – সহগ
3 – পদ
4 – প্রক্রিয়া চিহ্ন
5 – ধ্রুবক পদ
x y c – চলক/ধ্রুবক
প্রাথমিক বীজগণিত বীজগণিতের সর্বাধিক প্রাথমিক রূপ।এটা ঐ সকল ছাত্রদের শেখানো হয় যাদের পাটিগণিতের সাধারণ নীতিসমূহের বাইরে গণিতের কোন ধারণা নেই। পাটিগণিতে , কেবলমাত্র সংখ্যা এবং পাটিগণিত সংক্রান্ত প্রক্রিয়া চিহ্ন (যেমন +, −, ×, ÷) ব্যবহার করা হয়ে থাকে । বীজগণিতে , সংখ্যা অনেক সময় চলক এর মাধ্যমে প্রকাশ করা হয় (যেমন a, n, x, y অথবা z)। এটা খুবই গুরুত্বপূর্ণ কারণ :
- এটি পাটিগণিতের সূত্রসমূহের সাধারণ সূত্রে পরিণত করতে সাহায্য করে (যেমনঃ a + b = b + a;যা সকল a এবং b এর জন্য সত্য ) এবং বাস্তব সংখ্যার সিস্টেমের ধর্ম সমূহের পর্যায়ক্রমিক আবিষ্কারের এটি প্রথম পদক্ষেপ ছিল।
- এটি "অজানা" সংখ্যা সম্পর্কে ধারণা , সমীকরণের সূচনা এবং এগুলি কীভাবে সমাধান করা যাবে; সে বিষয়ে অধ্যয়নের অনুমতি দেয়। (উদাহরণস্বরূপ, "একটি সংখ্যা x বের কর, যাতে 3x + 1 = 10 হয়"। অথবা, আরও কিছুটা এগিয়ে "একটি সংখ্যা x বের কর যাতে ax + b =c হয় " । এটি আমাদের এই সিদ্ধান্তে নিয়ে যায় যে, নির্দিষ্ট সংখ্যার প্রকৃতির নয়, যা আমাদের সমীকরণটি সমাধান করতে দেয়। বরং এক্ষেত্রে সমীকরণ এর অন্তর্ভুক্ত অপারেশনগুলিই মুখ্য ভূমিকা পালন করে থাকে ।
- এটি ফাংশনসম্পর্কিত সম্পর্ক গঠন করতে অনুমতি দেয়। (উদাহরণস্বরূপ , "যদি তুমি x টিকিট বিক্রি করো , তবে তোমার মুনাফা হবে 3x − 10 টাকা , অথবা f(x) = 3x − 10, সেখানে f হল ফাংশন , এবং x হল ঐ সংখ্যা যার উপর ফাংশনটি কাজ করছে। ")
বহুপদী

একটি বহুপদী হলো এমন একটি রাশি যা সসীম সংখ্যক অশূন্য পদের যোগফল , যেখানে প্রত্যেক পদ ধ্রুবক এবং পূর্ণসাংখ্যিক ঘাতে উন্নত সসীম সংখ্যক চলকের গুণফল ধারণ করে। উদাহরণস্বরূপ , x2 + 2x − 3;একটি x চলকবিশিষ্ট বহুপদী। একটি বহুপদী রাশি হলো এমন একটি রাশি যাকে বিনিময় বিধি ,সংযোজন বিধি ,যোগ এবং গুণের বণ্টন বিধি দ্বারা বহুপদী হিসেবে পুনরায় লেখা যেতে পারে। উদাহরণস্বরূপ, (x− 1)(x + 3) হলো একটি বহুপদী রাশি।আসলে, সঠিকভাবে বলতে গেলে , এটি কিন্তু বহুপদী রাশি না। একটি বহুপদী ফাংশন হল এমন একটি ফাংশন যা বহুপদী , অথবা , একইভাবে , একটি বহুপদী রাশি দ্বারা সংজ্ঞায়িত। পূর্ববর্তী দুটি উদাহরণ একই বহুপদী ফাংশনকে সংজ্ঞায়িত করে।
দুটি গুরুত্বপূর্ণ এবং সম্পর্কিত বীজগাণিতিক সমস্যা হল বহুপদীর উৎপাদকে বিশ্লেষণ ,যাতে কোন বহুপদীকে অপর এক বা একাধিক বহুপদীর গুণফল আকারে প্রকাশ করা হয়,যাদের আর উৎপাদকে বিশ্লেষণ করা যাবে না , এবং বহুপদীর গরিষ্ঠ সাধারণ গুণনীয়ক নির্ণয়। উপরে উদাহরণে বর্ণিত বহুপদীটিকে (x − 1)(x + 3) আকারে উৎপাদকে বিশ্লেষণ করা সম্ভব। একই ধরনের সম্পর্কিত একটি সমস্যা হল এক চলকবিশিষ্ট বহুপদীর বর্গমূলের জন্য বীজগাণিতিক রাশি নির্ণয় করা।
বিমূর্ত বীজগণিত
বিমূর্ত বীজগণিত প্রাথমিক বীজগণিতে প্রাপ্ত পরিচিত ধারণাসমূহ এবং সংখ্যার পাটিগণিতকে সাধারণ ধারণায় আরও বিস্তৃত করে । নিম্নে বিমূর্ত বীজগণিতের মৌলিক ধারণাসমূহ তালিকাভুক্ত করা হয়েছে।
সেট: কেবলমাত্র বিভিন্ন ধরনের সংখ্যা বিবেচনা করার পরিবর্তে , বিমূর্ত বীজগণিত সেটের আরও সাধারণ ধারণা নিয়ে কাজ করে সেট : সকল বস্তুসমূহের একটি সংগ্রহ (যাদের উপাদান নামে ডাকা হয়)যা সেটের জন্য নির্দিষ্ট করা শর্তের ভিত্তিতে বেছে নেওয়া হয়।একই জাতীয় সকল সংখ্যাসমূহের সংগ্রহই হলো সেট। সেটের অন্যান্য উদাহরণগুলোর মধ্যে রয়েছে সকল ২×২ আকারের ম্যাট্রিক্স ,সকল দ্বিঘাত বিশিষ্ট বহুপদী (ax2 + bx + c) এর সেট ,একই সমতলে অবস্থিত সকল দুই মাত্রার ভেক্টরসমূহের সেট এবং বৃত্তাকার গ্রুপের মতো বিভিন্ন ধরনের সসীম গ্রুপ , যা পূর্ণসংখ্যার মডুলার n এর গ্রুপ। সেট তত্ত্ব যুক্তিবিদ্যার একটি শাখা এবং প্রায়োগিকভাবে বলতে গেলে এটি বীজগণিতের শাখা নয়।
বাইনারি অপারেশন :বাইনারি যোগ এর জন্য বলতে গেলে ∗, যোগের ধারণাটি আলাদা করে তুলে আনা হয়েছে। যে সেটের উপর অপারেশনটি সংজ্ঞায়িত তাছাড়া বাইনারি যোগের ধারণা অর্থহীন। S সেটের দুটি উপাদান a এবং b এর জন্য , a ∗ b সেটের মধ্যে অন্তর্ভুক্ত আরেকটি উপাদান ; এই শর্তটিকে বলা হয় আবদ্ধকরণ। যোগ (+), বিয়োগ (−), গুণ (×), ভাগ বায়োনারি অপারেশন হতে পারে যদি তা বিভিন্ন সিটের উপর সংজ্ঞায়িত করা হয় ,যেমনঃ ম্যাট্রিক্স, ভেক্টর, বহুপদীর যোগ এবং গুনের মতো।
অভেদক উপাদান :কোন অপারেশনে অভেদক উপাদানের ধারণা দেওয়ার জন্য ০ এবং ১ কে পৃথক করা হয়েছে। ০ যোগের জন্য অভেদক উপাদান এবং ১ গুণের জন্য অভেদক উপাদান। একটি সাধারণ বাইনারি অপারেটর ∗ এর জন্য অভেদক উপাদানটি হল e যা অবশ্যই a ∗ e = a এবং e ∗ a = a,এবং যদি এর অস্তিত্ব থাকে,তবে অবশ্যই এটিকে অনন্য হতে হবে। এটি যোগের জন্য এভাবে কাজ করে a + 0 = a এবং 0 + a = a এবং গুণের জন্য এভাবে a × 1 = a এবং 1 × a = a ।সকল সেট এবং অপারেটরসমূহের সমাবেশের অভেদক উপাদান থাকে না ; উদাহরণস্বরূপ , স্বাভাবিক ধনাত্মক সংখ্যার সেটটি হলো (1, 2, 3, ...) যার যোগের জন্য কোন অভেদক উপাদান নেই।
বিপরীত্মক উপাদান :ঋণাত্মক সংখ্যা প্রথম বিপরীত্মক উপাদান এর ধারণাটি তুলে ধরে।. যোগের জন্য , a এর বিপরীত্মককে লেখা হয় −a, এবং গুণাত্মক বিপরীত্মককে লেখা হয় a−1। a−1একটি সাধারণ উভধর্মী বিপরীত্মক উপাদান ,যা a ∗ a−1 = e এবং a−1 ∗ a = e এই ধর্মটিকে সমর্থন করে, যেখানে e একটি অভেদক উপাদান।
সহযোজন বিধি :পূর্ণসংখ্যার যোগফলের একটি ধর্ম রয়েছে একে সহযোজন বিধি বলে।এটিতে মূলত,সংখ্যাসমূহের গ্রুপ করা হয় যাতে যোগফলের মানের কোনো পরিবর্তন হয় না। উদাহরণস্বরূপ : (2 + 3) + 4 = 2 + (3 + 4)। সাধারণ অর্থে , (a ∗ b) ∗ c = a ∗ (b ∗ c) হয়ে থাকে।এই ধর্মটি অধিকাংশ বাইনারি অপারেশনে ব্যবহার করা হয়,কিন্তু বিয়োগ অথবা ভাগ অথবা অক্টোনিয়ান গুণ বাইনারি অপারেশনে ব্যবহার করা হয় না।
বিনিময় বিধি: বাস্তব সংখ্যার যোগ এবং গুণ উভয়ই বিনিময়যোগ্য। এক্ষেত্রে , সংখ্যার অবস্থানের ক্রম ফলাফলকে প্রভাবিত করে না। উদাহরণস্বরূপ : 2 + 3 = 3 + 2. সাধারণ অর্থে , a ∗ b = b ∗ aহয়ে থাকে। এই ধর্মটি সকল বাইনারি অপারেশনের জন্য কাজ করে না। উদাহরণস্বরূপ, ম্যাট্রিক্স গুণ এবং কোয়াটারনিয়ন গুণ উভয়ই অ-বিনিময়যোগ্য।
গ্রুপ
উপর্যুক্ত ধারণাসমূহকে একত্রিত করে গণিতের একটি গুরুত্বপূর্ণ কাঠামো গঠিত হয় : a গ্রুপ।একটা গ্রুপ হলো একটি সেট S এবং একটি বাইনারি অপারেটর ∗ এর সমাবেশ , তুমি যেভাবেই সংজ্ঞায়িত করো না কেন , কিন্তু নিম্নোক্ত ধর্মসমূহ তার মধ্যে থাকতে হবে :
- একটি অভেদক উপাদান e এর অস্তিত্ব রয়েছে , যেন S এর অন্তর্ভুক্ত প্রত্যেক সদস্য a এর জন্য , e ∗ a এবং a ∗ e উভয়ই a এর প্রতি অভিন্ন হয় ।
- প্রত্যেক উপাদানের একটি বিপরীত্মক রয়েছে : S এর অন্তর্ভুক্ত প্রত্যেক সদস্য a এর জন্য, একটি সংখ্যা a−1 রয়েছে; যেন a ∗ a−1 এবং a−1 ∗ a উভয়ই অভেদক উপাদানের প্রতি অভিন্ন।
- সংযোজন বিধি : যদি a, b এবং c ;S সেটের সদস্য হয়ে থাকে। তবে (a ∗ b) ∗ c এবং a ∗ (b ∗ c) অভিন্ন।
যদি একটি গ্রুপও বিনিময়যোগ্য হয় – যাতে, S এর অন্তর্ভুক্ত যেকোনো দুটি উপাদান a এবং b এর জন্য , a ∗ b এবং b ∗ a অভিন্ন হলে –এই গ্রুপটিকে বলা হবে আবেলিয়ান
উদাহরণস্বরূপ, যোগ অপারেশনের অধীনে সকল পূর্ণ সংখ্যার সেট একটি গ্রুপ। এই গ্রুপটিতে , অভেদক উপাদানটি হলো 0 এবং যেকোনো উপাদান a এর বিপরীত্মক হলো এর ঋণাত্মক , −a। সহযোজন বিধিটি ব্যবহারের জন্য প্রয়োজনীয় উপাদানের পূর্ণতা অর্জিত হয়েছে ,কারণ যেকোন পূর্ণ সংখ্যা a, b এবং cএর জন্য, (a + b) + c = a + (b + c)
অশূন্য মূলদ সংখ্যা গুনের অধীনে একটি গ্রুপ তৈরি করে। এখানে , 1 হল অভেদক উপাদান , যেহেতু যেকোনো মূলদ সংখ্যা a এর জন্য 1 × a = a × 1 = a। a এর বিপরীত্মক হলো 1/a, যেহেতু a × 1/a = 1.
যদিও, পূর্ণসংখ্যা গুন অপারেশনের অধীনে গ্রুপ তৈরি করে না। এটা এ কারণে যে,সাধারণত ,একটি পূর্ণসংখ্যার গুণাত্মক বিপরীত্মক পূর্ণসংখ্যা হয় না। উদাহরণস্বরূপ , 4 একটি পূর্ণ সংখ্যা , কিন্তু এর গুণাত্মক বিপরীত্মক সংখ্যা হলো ¼, যা পূর্ণসংখ্যা নয়।
গ্রুপ তত্ত্বে গ্রুপ সমূহের তথ্য নিয়ে অধ্যয়ন করা হয়। সসীম সাধারণ গ্রপসমূহের শ্রেণিবিভাগ হচ্ছে এ তত্ত্বের একটি বড় ফলাফল , যার অধিকাংশ ১৯৫৫ এবং ১৯৮৩ এর মধ্যে প্রকাশিত হয়েছিল ,যা সসীম সাধারণ গ্রুপকে আপাতত ৩০টি মূল ধরনে বিভক্ত করে।
অর্ধ-গ্রুপ , কোয়াসি-গ্রুপ, এবং মনোয়েড এর গঠন কাঠামো গ্রুপের মত , তবে আরও সাধারণ ধরনের।এরা সেট এবং একটি বদ্ধ বাইনারি অপারেশন গঠন করে কিন্তু অন্যান্য শর্তগুলো প্রয়োজনমতো পূরণ করে না। একটি অর্ধ-গ্রুপের একটি সহযোজন বাইনারি অপারেশন রয়েছে কিন্তু এটির অভেদক উপাদান নাও থাকতে পারে। একটি মনোয়েড হলো একটি অর্ধ-গ্রুপ যার একটি অভেদক রয়েছে কিন্তু প্রত্যেক উপাদানের জন্য বিপরীত্মক নাও থাকতে পারে। একটি কোয়াসি-গ্রুপ একটি প্রয়োজন পূরণ করে, যাতে একটি উপাদানকে ওপর আরেকটি উপাদানে হয় অনন্য বাম-গুণ অথবা ডান-গুণ দ্বারা পরিণত করা যেতে পারে। ; যদিও , বাইনারি অপারেশনটি সহযোজন যোগ্য নাও হতে পারে।
সকল গ্রুপগুলো হলো মনোয়েড এবং সকল মনোয়েড হলো অর্ধ-গ্রুপ।
| সেট | স্বাভাবিক সংখ্যা N | পূর্ণসংখ্যা Z | মূলদ সংখ্যা Q (আরও বাস্তব সংখ্যা R এবং জটিল সংখ্যা C ) | পূর্ণসংখ্যা মডুলিয়ান 3: Z3 = {0, 1, 2} | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| অপারেশন | + | × (w/o শূন্য ) | + | × (w/o শূন্য) | + | − | × (w/o শূন্য) | ÷ (w/o শূন্য) | + | × (w/o শূন্য) |
| বদ্ধ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ |
| অভেদক | 0 | 1 | 0 | 1 | 0 | N/A | 1 | N/A | 0 | 1 |
| বিপরীত্মক | N/A | N/A | −a | N/A | −a | N/A | 1/a | N/A | যথাক্রমে, 0, 2, 1 | যথাক্রমে, N/A, 1, 2 |
| সহযোজনযোগ্য | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | না | হ্যাঁ | না | হ্যাঁ | হ্যাঁ |
| বিনিময়যোগ্য | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | হ্যাঁ | না | হ্যাঁ | না | হ্যাঁ | হ্যাঁ |
| গঠন | মনোয়েড | মনোয়েড | আলেবিয়ান গ্রুপ | মনোয়েড | আলেবিয়ান গ্রুপ | কোয়াসি-গ্রুপ | আলেবিয়ান গ্রুপ | কোয়াসি-গ্রুপ | আলেবিয়ান গ্রুপ | আলেবিয়ান গ্রুপ (Z2) |
রিং এবং ক্ষেত্র
গ্রুপ সমূহের কেবল একটি মাত্র বাইনারি অপারেশন রয়েছে। বিভিন্ন ধরনের সংখ্যা এবং কাঠামো সম্পূর্ণভাবে ব্যাখ্যার জন্য দুটি অপারেটর সম্পর্কে অধ্যয়ন করা একান্ত প্রয়োজন। এই তত্ত্বসমূহের মধ্যে সবচেয়ে গুরুত্বপূর্ণ দুটি তত্ত্ব হলো রিং তত্ত্ব এবং ক্ষেত্র তত্ত্ব।
একটি রিংয়ের দুটি বাইনারি অপারেটর (+) এবং (×) রয়েছে। যেখানে, × , + এর সাথে বণ্টনযোগ্য। প্রথম অপারেটর (+) এর অধীনে এটি আবেলিয়ান গ্রুপ গঠন করে। দ্বিতীয় অপারেটর (×) এর অধীনে এটি সংযোজনযোগ্য , কিন্তু এটির অভেদক অথবা বিপরীত্বক থাকার কোন দরকার নেই , সুতরাং ভাগের কোন দরকার নেই। যোগাত্মক(+) অভেদক উপাদানটিকে লেখা হয় 0 এবং a এর যোগাত্মক বিপরীত্বককে লেখা হয় −a।
বণ্টনযোগ্যতা বণ্টন সূত্রকে সংখ্যার জন্য সাধারণ করে। পূর্ণসংখ্যার জন্য (a + b) × c = a × c + b × c এবং c × (a + b) = c × a + c × b, এবং × কে + এর সাথে বণ্টনযোগ্য বলা হয়ে থাকে।
পূর্ণসংখ্যাসমূহ রিং এর একটি উদাহরণ। পূর্ণসংখ্যাসমূহের একটি অতিরিক্ত ধর্ম রয়েছে যা তাকে পূর্ণসাংখ্যিক ডোমেইন এ পরিণত করেছে।
একটি ক্ষেত্র হল অতিরিক্ত ধর্মসহ একটি রিং যাতে 0 বাদে সকল উপাদান × এর অধীনে একটি আবেলিয়ান গ্রুপ গঠন করে । a এর গুণাত্বক (×) অভেদককে লেখা হয় 1 এবং a এর গুণাত্বক বিপরীত্বককে লেখা হয় a−1।
মূলদ সংখ্যাসমূহ , বাস্তব সংখ্যাসমূহ এবং জটিল সংখ্যাসমূহ সবই ক্ষেত্র(ফিল্ড) এর উদাহরণ।
বহিঃসংযোগ




- খান একাডেমি: ধারণামূলক ভিডিও এবং কাজের উদাহরণ
- খান একাডেমি: বীজগণিতের উৎপত্তি , বিনামূল্যে অনলাইন ক্ষুদ্র লেকচার
- অ্যালজেবরা রুলস ডটকম: বীজগণিতের মৌলিক বিষয়গুলি শেখার জন্য একটি মুক্ত উৎস
- বীজগণিতের ৪০০০ বছর,গ্রিশাম কলেজে, রবিন উইলসনের বক্তৃতা, অক্টোবর ১৭, ২০০৭ (এমপি৩ এবং এমপি৪ ডাউনলোডের জন্য উপলব্ধ, পাশাপাশি একটি টেক্সট ফাইল হিসেবেও)।
বীজগণিত বীজগণিত • মেট্রিক্স • নির্ণায়ক • বহুপদী • বীজগাণিতিক সমীকরণ • ফিল্ড • গ্যালোয়ার তত্ত্ব • যোগাশ্রয়ী জগৎ • রিং • সহযোগী বীজগণিত • বিনিমেয় রিং • ন্যোথারীয় রিং • বহুপদীর রিং • ঘাত ধারার রিং • দ্বিঘাত বহুপদী • ক্লিফোর্ড বীজগণিত • অন্তরক রিং • ভিট ভেক্টর • মান আরোপন • আদেলীয় গ্রুপ • কেলি বীজগণিত • জর্ডান বীজগণিত • মডিউল • হোমোলজীয় বীজগণিত • হপ্ফ্ বীজগণিত |
আরও দেখুন
- বীজগণিতের রূপরেখা
- রৈখিক বীজগণিতের রূপরেখা
- বীজগাণিতিক টাইল
- সেট
- বহুপদী
- বহুপদী সমীকরণ
- দ্বিপদী উপপাদ্য
আরও পড়ুন
- Allenby, R. B. J. T. (১৯৯১)। Rings, Fields and Groups। আইএসবিএন 0-340-54440-6।
- Asimov, Isaac (১৯৬১)। Realm of Algebra। Houghton Mifflin।
- Euler, Leonhard (নভেম্বর ২০০৫)। Elements of Algebra। আইএসবিএন 978-1-899618-73-6। ২০১১-০৪-১৩ তারিখে মূল থেকে আর্কাইভ করা।
- Herstein, I. N. (১৯৭৫)। Topics in Algebra
 । আইএসবিএন 0-471-02371-X।
। আইএসবিএন 0-471-02371-X। - Hill, Donald R. (১৯৯৪)। Islamic Science and Engineering। Edinburgh University Press।
- Joseph, George Gheverghese (২০০০)। The Crest of the Peacock: Non-European Roots of Mathematics। Penguin Books।
- O'Connor, John J.; Robertson, Edmund F. (২০০৫)। "History Topics: Algebra Index"। MacTutor History of Mathematics archive। University of St Andrews। ২০১৬-০৩-০৩ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ ২০১১-১২-১০।
- Sardar, Ziauddin; Ravetz, Jerry; Loon, Borin Van (১৯৯৯)। Introducing Mathematics। Totem Books।
তথ্যসূত্র
This article uses material from the Wikipedia বাংলা article বীজগণিত, which is released under the Creative Commons Attribution-ShareAlike 3.0 license ("CC BY-SA 3.0"); additional terms may apply (view authors). বিষয়বস্তু সিসি বাই-এসএ ৪.০-এর আওতায় প্রকাশিত যদি না অন্য কিছু নির্ধারিত থাকে। Images, videos and audio are available under their respective licenses.
®Wikipedia is a registered trademark of the Wiki Foundation, Inc. Wiki বাংলা (DUHOCTRUNGQUOC.VN) is an independent company and has no affiliation with Wiki Foundation.










