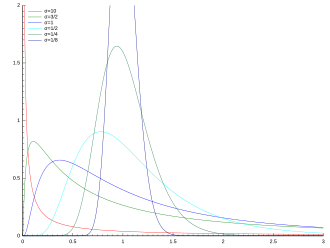
Logarithmische Normalverteilung: Häufige Zufallsverteilung bei Größen, die beliebige positive Werte annehmen können

Sie beschreibt die Verteilung einer Zufallsvariablen ${\displaystyle X}$, wenn die mit dem Logarithmus transformierte Zufallsvariable ${\displaystyle Y=\ln(X)}$ normalverteilt ist. Sie bewährt sich als Modell für viele Messgrößen in Naturwissenschaften, Medizin und Technik, beispielsweise für Energien, Konzentrationen, Längen und Mengenangaben.

In Analogie zu einer normalverteilten Zufallsvariablen, die nach dem zentralen Grenzwertsatz als Summe vieler verschiedener Zufallsvariablen aufgefasst werden kann, entsteht eine logarithmisch normalverteilte Zufallsvariable durch das Produkt vieler positiver Zufallsvariablen. Somit ist die Log-Normalverteilung die einfachste Verteilungsart für multiplikative Zufallsprozesse. Da multiplikative Gesetze in den Naturwissenschaften, der Ökonomie und der Technik eine größere Rolle spielen als additive, ist die Log-Normalverteilung in vielen Anwendungen diejenige, die der Theorie am besten entspricht – der zweite Grund, weshalb sie vielfach anstelle der gewöhnlichen, additiven Normalverteilung verwendet werden sollte.

 

Erzeugung

Wenn ${\displaystyle Z}$  eine standardnormalverteilte Zufallsvariable ist, dann ist ${\displaystyle X=\mathrm {e} ^{\mu +\sigma Z}=\mathrm {e} ^{\mu }(\mathrm {e} ^{Z})^{\sigma }}$  log-normalverteilt mit den Parametern ${\displaystyle \mu }$  und ${\displaystyle \sigma >0}$ , geschrieben als ${\displaystyle {\mathcal {LN}}(\mu ,\sigma ^{2})}$ . Alternativ können als Parameter die Größen ${\displaystyle \mu ^{*}=\mathrm {e} ^{\mu }}$  und ${\displaystyle \sigma ^{*}=\mathrm {e} ^{\sigma }>1}$  verwendet werden. ${\displaystyle \mu ^{*}}$  ist ein Skalen-Parameter. ${\displaystyle \sigma }$  oder ebenso ${\displaystyle \sigma ^{*}}$  bestimmt die Form der Verteilung.

Wenn ${\displaystyle X}$  log-normalverteilt ist, dann ist auch ${\displaystyle Y=aX}$  log-normalverteilt, und zwar mit den Parametern ${\displaystyle \ln(a)+\mu }$  und ${\displaystyle \sigma }$  respektive ${\displaystyle a\mu ^{*}}$  und ${\displaystyle \sigma ^{*}}$ . Ebenso ist ${\displaystyle X^{b}}$  log-normalverteilt, mit den Parametern ${\displaystyle b\mu }$  und ${\displaystyle b\sigma }$  respektive ${\displaystyle (\mu ^{*})^{b}}$  und ${\displaystyle (\sigma ^{*})^{b}}$ .

Dichtefunktion

Eine stetige, positive Zufallsvariable ${\displaystyle X}$  unterliegt einer logarithmischen Normalverteilung ${\displaystyle {\mathcal {LN}}(\mu ,\sigma ^{2})}$  mit den Parametern ${\displaystyle \mu \in \mathbb {R} }$  und ${\displaystyle \sigma \in \mathbb {R} ,\sigma >0}$ , wenn die transformierte Zufallsvariable ${\displaystyle Y=\ln(X)}$  einer Normalverteilung ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$  folgt. Ihre Dichtefunktion ist dann

${\displaystyle f(x)={\frac {1}{{\sqrt {2\pi }}\sigma x}}\,\exp {\Big (}-{\frac {(\ln(x)-\mu )^{2}}{2\sigma ^{2}}}{\Big )}={\frac {1}{x\sigma }}\varphi \left({\frac {\ln(x)-\mu }{\sigma }}\right),\quad x>0}$ ,

wobei ${\displaystyle \varphi }$  die Dichtefunktion der Standardnormalverteilung bezeichnet.

Verteilungsfunktion

 

Damit hat die Log-Normalverteilung für ${\displaystyle x\geq 0}$  die Verteilungsfunktion

${\displaystyle F(x)=\int _{0}^{x}f(t)\,\mathrm {d} t=\Phi \left({\frac {\ln(x)-\mu }{\sigma }}\right)}$ ,

wobei ${\displaystyle \Phi }$  die Verteilungsfunktion der Standardnormalverteilung bezeichnet.

Die Verteilungsfunktion der logarithmischen Normalverteilung erscheint auf logarithmisch geteiltem Wahrscheinlichkeitspapier als Gerade.

Mehrdimensionale log-Normalverteilung

Sei ${\displaystyle {\boldsymbol {Z}}\sim {\mathcal {N}}({\boldsymbol {\mu }},\,{\boldsymbol {\Sigma }})}$  ein mehrdimensional (oder multivariat) normalverteilter Zufallsvektor. Dann ist ${\displaystyle {\boldsymbol {X}}=\exp({\boldsymbol {Z}})}$  (d. h. ${\displaystyle X_{j}=\exp(Z_{j})}$ ) multivariat log-normalverteilt. Die mehrdimensionale Log-Normalverteilung ist viel weniger bedeutsam als die eindimensionale. Deshalb bezieht sich der nachfolgende Text fast ausschließlich auf den eindimensionalen Fall.

Quantile

Ist ${\displaystyle u_{(p)}}$  das p-Quantil einer Standardnormalverteilung (d. h. ${\displaystyle \Phi (u_{(p)})=p}$ , wobei ${\displaystyle \Phi }$  die Verteilungsfunktion der Standardnormalverteilung sei), so ist das p-Quantil der Log-Normalverteilung gegeben durch

${\displaystyle x_{(p)}=\mathrm {e} ^{\mu +u_{(p)}\cdot \sigma }}$ .

Median, multiplikativer Erwartungswert

Der Median der logarithmischen Normalverteilung beträgt demnach ${\displaystyle \mu ^{*}=\mathrm {e} ^{\mu }}$ . Er wird auch multiplikativer oder geometrischer Erwartungswert genannt (vgl. geometrisches Mittel). Er ist ein Skalen-Parameter, da ${\displaystyle \mu ^{*}(aX)=a\mu ^{*}(X)}$  gilt.

Multiplikative Standardabweichung

In Analogie zum multiplikativen Erwartungswert ist ${\displaystyle \sigma ^{*}=\mathrm {e} ^{\sigma }}$  die multiplikative oder geometrische Standardabweichung. Sie bestimmt (ebenso wie ${\displaystyle \sigma }$  selbst) die Form der Verteilung. Es gilt ${\displaystyle \sigma ^{*}>1}$ .

Da das multiplikative oder geometrische Mittel einer Stichprobe von lognormalen Beobachtungen (siehe „Parameterschätzung“ unten) selbst log-normalverteilt ist, kann man seine Standardabweichung angeben, sie beträgt ${\displaystyle (\sigma ^{*})^{1/{\sqrt {n}}}}$ .

Erwartungswert

Der Erwartungswert der logarithmischen Normalverteilung beträgt

${\displaystyle \operatorname {E} (X)=\mathrm {e} ^{\mu +{\frac {\sigma ^{2}}{2}}}}$ .

Modus

Der Modus, also der häufigste Wert der Verteilung bzw. der Wert, für den die Dichtefunktion ihr Maximum annimmt, beträgt für die logarithmische Normalverteilung

${\displaystyle \operatorname {Modus} (X)=x_{D}=\mathrm {e} ^{\mu -\sigma ^{2}}}$ .

Varianz, Standardabweichung, Variationskoeffizient

Die Varianz ergibt sich zu

${\displaystyle \operatorname {Var} (X)=\mathrm {e} ^{2\mu +\sigma ^{2}}(\mathrm {e} ^{\sigma ^{2}}-1)}$ .

Für die Standardabweichung ergibt sich

${\displaystyle {\sqrt {\operatorname {Var} (X)}}={\sqrt {\mathrm {e} ^{2\mu +\sigma ^{2}}(\mathrm {e} ^{\sigma ^{2}}-1)}}=\mathrm {e} ^{\mu +{\frac {\sigma ^{2}}{2}}}\cdot {\sqrt {\mathrm {e} ^{\sigma ^{2}}-1}}}$ .

Aus Erwartungswert und Varianz erhält man unmittelbar den Variationskoeffizienten

${\displaystyle \operatorname {VarK} (X)={\sqrt {\mathrm {e} ^{\sigma ^{2}}-1}}}$ .

Schiefe

Die Schiefe ergibt sich zu

${\displaystyle \gamma _{m}=(\mathrm {e} ^{\sigma ^{2}}+2){\sqrt {\mathrm {e} ^{\sigma ^{2}}-1}}>0}$ ,

d. h., die Log-Normalverteilung ist rechtsschief.

Je größer die Differenz zwischen Erwartungswert und Median, desto ausgeprägter ist i. a. die Schiefe einer Verteilung. Hier unterscheiden sich diese Parameter um den Faktor ${\displaystyle \mathrm {e} ^{\sigma ^{2}/2}}$ . Die Wahrscheinlichkeit für extrem große Ausprägungen ist also bei der Log-Normalverteilung mit großem ${\displaystyle \sigma }$  hoch.

Momente

Es existieren alle Momente und es gilt:

${\displaystyle \operatorname {E} (X^{n})=\mathrm {e} ^{n\mu +{\frac {n^{2}\sigma ^{2}}{2}}},\quad n\in \mathbb {N} }$ .

Die momenterzeugende Funktion und die charakteristische Funktion existieren für die Log-Normalverteilung nicht in expliziter Form.

Die Lognormalverteilung ist ein Beispiel einer Wahrscheinlichkeitsverteilung, die durch die Angabe aller Momente nicht charakterisiert ist, da es andere Wahrscheinlichkeitsverteilungen mit denselben Momenten gibt.

Entropie

Die Entropie der logarithmischen Normalverteilung (ausgedrückt in nats) beträgt

${\displaystyle \mu +{\frac {1}{2}}\ln \left(2\pi \mathrm {e} \sigma ^{2}\right)}$ .

Multiplikation von unabhängigen, log-normalverteilten Zufallsvariablen

Multipliziert man zwei unabhängige, log-normalverteilte Zufallsvariable ${\displaystyle X_{1}}$  und ${\displaystyle X_{2}}$ , so ergibt sich wieder eine log-normalverteilte Zufallsvariable mit den Parametern ${\displaystyle \mu =\mu _{1}+\mu _{2}}$  und ${\displaystyle \sigma }$ , wobei ${\displaystyle \sigma ^{2}=\sigma _{1}^{2}+\sigma _{2}^{2}}$ . Entsprechendes gilt für das Produkt von ${\displaystyle n}$  solchen Variablen.

Grenzwertsatz

Das geometrische Mittel von ${\displaystyle n}$  unabhängigen, gleich verteilten, positiven Zufallsvariablen zeigt für ${\displaystyle n\to \infty }$  genähert eine Log-Normalverteilung, die immer mehr einer gewöhnlichen Normalverteilung gleicht, da ${\displaystyle \sigma }$  abnimmt.

Erwartungswert und Kovarianzmatrix einer mehrdimensionalen Log-Normalverteilung

Der Erwartungswert-Vektor ist

${\displaystyle \operatorname {E} [{\boldsymbol {X}}]_{i}=\mathrm {e} ^{\mu _{i}+{\frac {1}{2}}\Sigma _{ii}}}$ 

und die Kovarianzmatrix

${\displaystyle \operatorname {Var} [{\boldsymbol {X}}]_{ij}=\mathrm {e} ^{\mu _{i}+\mu _{j}+{\frac {1}{2}}(\Sigma _{ii}+\Sigma _{jj})}(\mathrm {e} ^{\Sigma _{ij}}-1).}$ 

Beziehung zur Normalverteilung

Der Logarithmus einer logarithmisch normalverteilten Zufallsvariablen ist normalverteilt. Genauer: Ist ${\displaystyle Y}$  eine ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$ -verteilte reelle Zufallsvariable (d. h. normalverteilt mit Erwartungswert ${\displaystyle \mu }$  und Varianz ${\displaystyle \sigma ^{2}}$ ), so ist die Zufallsvariable ${\displaystyle X=\mathrm {e} ^{Y}}$  log-normalverteilt mit diesen Parametern ${\displaystyle \mu }$  und ${\displaystyle \sigma }$ .

Wenn ${\displaystyle \sigma \to 0}$  und damit ${\displaystyle \sigma ^{*}\to 1}$  geht, geht die Form der Log-Normalverteilung gegen diejenige einer gewöhnlichen Normalverteilung.

Verteilung mit schweren Rändern

Die Verteilung gehört zu den Verteilungen mit schweren Rändern.

Parameterschätzung

Die Schätzung der Parameter aus einer Stichprobe von Beobachtungen erfolgt über die Bestimmung von Mittelwert und (quadrierter) Standardabweichung der logarithmierten Werte:

${\displaystyle {\hat {\mu }}={\frac {1}{n}}\sum _{i=1}^{n}\ln(X_{i}),\quad {\hat {\sigma }}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(\ln(X_{i})-{\hat {\mu }})^{2}}$ .

Die Schätzung der multiplikativen Parameter erfolgt durch ${\displaystyle {\hat {\mu }}^{*}=\exp({\hat {\mu }})}$  und ${\displaystyle {\hat {\sigma }}^{*}=\exp({\hat {\sigma }})}$ . ${\displaystyle {\hat {\mu }}^{*}}$  ist das geometrische Mittel. Seine Verteilung ist log-normal mit multiplikativem Erwartungswert ${\displaystyle \mu ^{*}}$  und geschätzter multiplikativer Standardabweichung (besser als multiplikativer Standardfehler bezeichnet) ${\displaystyle \mathrm {SEM} ^{*}=({\hat {\sigma }}^{*})^{1/{\sqrt {n}}}}$ .

Wenn keine Einzelwerte vorliegen, sondern nur der Mittelwert ${\displaystyle {\bar {X}}}$  und die empirische Varianz ${\displaystyle {\hat {\mathrm {var} }}}$  der nicht logarithmierten Werte bekannt sind, erhält man passende Parameterwerte über

${\displaystyle {\hat {\sigma }}^{2}=\ln \left({\frac {\hat {\mathrm {var} }}{{\bar {X}}^{2}}}+1\right)}$ 
${\displaystyle {\hat {\mu }}=\ln({\bar {X}})-{\frac {{\hat {\sigma }}^{2}}{2}}}$  oder direkt ${\displaystyle \quad {\hat {\mu }}=\ln \left({\bar {X}}^{2}\ {\sqrt[{}]{\frac {1}{{\hat {\mathrm {var} }}+{\bar {X}}^{2}}}}\right)}$ .

Statistik

Allgemein erfolgt die statistische Analyse von log-normalverteilten Größen am einfachsten und Erfolg versprechendsten so, dass die Größen logarithmiert werden und auf diese transformierten Werte die Methoden verwendet werden, die auf der gewöhnlichen Normalverteilung beruhen. Im Bedarfsfall werden dann die Ergebnisse, beispielsweise Vertrauens- oder Vorhersage-Intervalle, in die ursprüngliche Skala zurücktransformiert.

Grundlegendes Beispiel dafür ist die Berechnung von Streuungs-Intervallen. Da für eine gewöhnliche Normalverteilung in einem Bereich von ${\displaystyle \mu \pm \sigma }$  etwa 2/3 (genauer 68 %) und in ${\displaystyle \mu \pm 2\sigma }$  95 % der Wahrscheinlichkeit enthalten sind, gilt für die Log-Normalverteilung:

Das Intervall ${\displaystyle \ [\mu ^{*}/\sigma ^{*},\mu ^{*}\cdot \sigma ^{*}]\ }$  enthält 2/3
und das Intervall ${\displaystyle \ [\mu ^{*}/(\sigma ^{*})^{2},\mu ^{*}\cdot (\sigma ^{*})^{2}]\ }$  enthält 95 %

der Wahrscheinlichkeit (und also etwa diese Prozentzahl der Beobachtungen einer Stichprobe). Die Intervalle können in Analogie zu ${\displaystyle \mu \pm \sigma }$  als ${\displaystyle \mu ^{*}\cdot /\sigma ^{*}}$  und ${\displaystyle \mu ^{*}\cdot /(\sigma ^{*})^{2}}$  notiert werden.

In graphischen Darstellungen (untransformierter) Beobachtungen sollten deshalb solche asymmetrische Intervalle gezeigt werden.

Variation in vielen natürlichen Phänomenen lässt sich gut mit der Log-Normalverteilung beschreiben. Dies kann erklärt werden durch die Vorstellung, dass kleine prozentuale Abweichungen zusammenwirken, die einzelnen Effekte sich also multiplizieren. Bei Wachstumsprozessen ist dies besonders naheliegend. Zudem bestehen die Formeln für die meisten grundlegenden Naturgesetze aus Multiplikationen und Divisionen. Auf der logarithmischen Skala ergeben sich dann Additionen und Subtraktionen, und der entsprechende Zentrale Grenzwertsatz führt zur Normalverteilung – zurücktransformiert auf die ursprüngliche Skala also zur Log-Normalverteilung. Diese multiplikative Version des Grenzwertsatzes ist auch als Gesetz von Gibrat bekannt. Robert Gibrat (1904–1980) formulierte es für Unternehmen.

In einigen Wissenschaften ist es üblich, Messgrößen in Einheiten anzugeben, die durch Logarithmieren einer gemessenen Konzentration (Chemie) oder Energie (Physik, Technologie) erhalten werden. So wird der Säuregrad einer wässerigen Lösung durch den pH-Wert gemessen, der als negativer Logarithmus der Wasserstoffionen-Aktivität definiert ist. Eine Lautstärke wird in Dezibel (dB) angegeben, das ${\displaystyle =10\log _{10}(E)}$ , wobei ${\displaystyle E}$  das Verhältnis des Schalldruckpegels zu einem entsprechenden Referenzwert ist. Analoges gilt für andere Energie-Pegel. In der Finanzmathematik wird ebenfalls oft direkt mit logarithmierten Größen (Preisen, Kursen, Erträgen) gerechnet, siehe unten.

Für solche „bereits logarithmierte“ Größen ist dann die gewöhnliche Normalverteilung oft eine gute Wahl; also wäre hier, wenn man die ursprünglich gemessene Größe betrachten wollte, die Log-Normalverteilung geeignet.

Generell eignet sich die Log-Normalverteilung für Messgrößen, die nur positive Werte annehmen können, also Konzentrationen, Massen und Gewichte, räumliche Größen, Energien usw.

Die folgende Liste zeigt mit Beispielen die breite Palette der Anwendungen der Log-Normalverteilung.

• Mathematik (Analytische Zahlentheorie): Selbergs zentraler Grenzwertsatz

• Geologie: Konzentration von Elementen

• Kolloid- und Polymerchemie: Partikelgrößen-Verteilung und Molmassen-Verteilung

• Hydrologie: Die Log-Normalverteilung nützt bei der Analyse von Extremwerten wie – beispielsweise – monatliche oder jährliche Maxima der täglichen Regenmenge oder des Abflusses von Gewässern.

• Ökologie: Die Häufigkeit von Arten zeigt oft eine Log-Normalverteilung.

• Biologie und Medizin
  • Maße der Größe von Lebewesen (Länge, Hautfläche, Gewicht);
  • Physiologische Größen wie der Blutdruck von Männern und Frauen. Als Konsequenz sollten Referenzbereiche für gesunde Werte auf der Grundlage einer Log-Normalverteilung geschätzt werden.
  • Inkubationszeiten von ansteckenden Krankheiten;
  • In der Neurologie zeigt die Verteilung der Impulsrate von Nervenzellen oft eine log-normale Form, so im Cortex und Striatum und im Hippocampus und im entorhinalen Cortex sowie in anderen Hirnregionen. Ebenso für weitere neurobiologische Größen.
  • Sensitivität gegenüber Fungiziden;
  • Bakterien auf Pflanzenblättern:
  • Permeabilität von Zellwänden und Mobilität von gelösten Stoffen:

• Sozialwissenschaften und Ökonomie
  • Einkommensverteilungen zeigen, bis auf wenige Extremwerte, eine genäherte Log-Normalverteilung. (Für das obere Ende eignet sich die Pareto-Verteilung.)
  • In der Finanzmathematik werden logarithmierte Erträge, Preise etc. als normalverteilt modelliert, was bedeutet, dass die ursprünglichen Größen log-normalverteilt sind. Das gilt auch für das berühmte Black-Scholes-Modell, das der Preisbildung von Optionen und Derivaten zugrunde liegt. Allerdings mag bei genauer Analyse die Lévy-Verteilung für die extrem großen Werte besser passen, vor allem bei Börsenstürzen.
  • Einwohnerzahlen von Städten
  • In Internet-Foren sind die Längen der Kommentare log-normalverteilt, ebenso die Verweildauer bei Online-Artikeln wie Nachrichten oder Witzen.
  • Die Dauer von Schachspielen folgt einer Log-Normalverteilung.

• Technologie
  • In der Modellierung der Zuverlässigkeit werden Reparaturzeiten als log-normalverteilt beschrieben.
  • Internet: Die Dateigröße von öffentlich verfügbaren Audio- und Video-Dateien ist genähert log-normalverteilt. Analoges gilt für den Datenverkehr.

• Lognormal Distributions, Theory and Applications (= Statistics: Textbooks and Monographs. Band 88). Marcel Dekker, Inc., 1988, ISBN 978-0-8247-7803-3, S. xvi+387. 
• j Aitchison, J A C Brown: The Lognormal Distribution. Cambridge University Press, 1957. 
• Eckhard Limpert, Werner A Stahel, Markus Abbt: Lognormal distributions across the sciences: keys and clues. In: BioScience. Band 51, Nr. 5, 2001, S. 341–352, doi:10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2 (PDF Online).