Primzahl: Natürliche Zahl, die nur die 1 und sich selbst als Teiler hat
Eine Primzahl (von lateinisch numerus primus ‚erste Zahl‘) ist eine natürliche Zahl, die genau zwei Teiler hat (und somit größer als 1 ist).
Diese zwei Teiler sind 1 und die Zahl selber. Dabei bedeutet primus speziell „Anfang, das Erste (der Dinge)“, sodass eine „Anfangszahl“ gemeint ist, die aus keiner anderen natürlichen Zahl multiplikativ konstruiert werden kann.

Die Menge der Primzahlen wird in der Regel mit dem Symbol bezeichnet. Man weiß durch den Satz des Euklid seit der Antike, dass es unendlich viele Primzahlen gibt. Mit verknüpft ist die Folge der nach ihrer Größe geordneten Primzahlen, die man auch Primzahlfolge nennt.
Die Primzahlen lassen sich unter anderem mit Hilfe der Teileranzahlfunktion definieren
Es ist demnach
mit


Die Bedeutung der Primzahlen für viele Bereiche der Mathematik beruht auf drei Folgerungen aus ihrer Definition:
- Existenz und Eindeutigkeit der Primfaktorzerlegung: Jede natürliche Zahl, die größer als 1 und selbst keine Primzahl ist, lässt sich als Produkt von mindestens zwei Primzahlen schreiben. Diese Produktdarstellung ist bis auf die Reihenfolge der Faktoren eindeutig. Zum Beweis dient das
- Lemma von Euklid: Ist ein Produkt zweier natürlicher Zahlen durch eine Primzahl teilbar, so ist mindestens einer der Faktoren durch sie teilbar.
- Primzahlen lassen sich nicht als Produkt zweier natürlicher Zahlen, die beide größer als 1 sind, darstellen.
Diese Eigenschaften werden in der Algebra für Verallgemeinerungen des Primzahlbegriffs genutzt.
Eine Zahl, die das Produkt von zwei oder mehr Primfaktoren ist, nennt man zusammengesetzt. Die Zahl 1 ist weder prim noch zusammengesetzt. Alle anderen natürlichen Zahlen sind eines von beiden, entweder prim (also Primzahl) oder zusammengesetzt.
Schon im antiken Griechenland interessierte man sich für die Primzahlen und entdeckte einige ihrer Eigenschaften. Obwohl Primzahlen seit damals stets einen großen Reiz auf die Menschen ausübten, sind viele die Primzahlen betreffenden Fragen bis heute ungeklärt, darunter solche, die mehr als hundert Jahre alt und leicht verständlich formulierbar sind. Dazu gehören die Goldbachsche Vermutung, wonach außer 2 jede gerade Zahl als Summe zweier Primzahlen darstellbar ist, und die Vermutung, dass es unendlich viele Primzahlzwillinge gibt (das sind Paare von Primzahlen, deren Differenz gleich 2 ist).
Primzahlen und ihre Eigenschaften spielen in der Kryptographie eine große Rolle, weil Primfaktoren auch mit dem Aufkommen elektronischer Rechenmaschinen nicht effizient gefunden werden können. Andererseits ermöglichen diese Maschinen eine effiziente Verschlüsselung sowie, wenn man den Schlüssel kennt, Entschlüsselung auch langer Texte.
Eigenschaften von Primzahlen
Die Primzahlen sind innerhalb der Menge 
Mit Ausnahme der Zahl 2 sind alle Primzahlen 


Jede Primzahl 










Jede Primzahl 



Darüber hinaus hat jede Primzahl 






Jede natürliche Zahl der Form 




Eine Primzahl 





im Ring der ganzen Gaußschen Zahlen.
Die Zahl −1 ist quadratischer Rest modulo jeder Primzahl der Form 

Eine Primzahl 




Ist eine Zahl 


Der kleine Satz von Fermat
Es sei 


Für nicht durch 

Es gibt Zahlen 






In diesem Zusammenhang zeigt sich die Problematik Fermatscher Pseudoprimzahlen: Sie werden von einem Primzahltest, der den kleinen Satz von Fermat nutzt (Fermatscher Primzahltest), fälschlicherweise für Primzahlen gehalten. Wenn allerdings ein Verschlüsselungsverfahren wie RSA eine zusammengesetzte Zahl statt einer Primzahl verwendet, ist die Verschlüsselung nicht mehr sicher. Deshalb müssen bei solchen Verfahren bessere Primzahltests verwendet werden.
Euler und das Legendre-Symbol
Eine einfache Folge aus dem kleinen Satz von Fermat ist: Für jede ungerade Primzahl 


oder
Man kann zeigen, dass der erste Fall genau dann eintritt, wenn es eine Quadratzahl gibt, die kongruent zu 

Binomialkoeffizient
Für Primzahlen 

Zusammen mit dem binomischen Satz folgt daraus
Für ganze Zahlen 


Aus dem Satz von Wilson (



erfüllt ist.
Charles Babbage bewies 1819, dass für jede Primzahl 
Der Mathematiker Joseph Wolstenholme (1829–1891) bewies dann 1862, dass für jede Primzahl 
Giuga
Aus dem kleinen Satz von Fermat folgt, dass für eine Primzahl 
Beispiel 
Giuseppe Giuga vermutete, dass auch die umgekehrte Schlussrichtung gilt, dass also eine Zahl mit dieser Eigenschaft stets prim ist. Es ist nicht geklärt, ob diese Vermutung richtig ist. Bekannt ist aber, dass ein Gegenbeispiel mehr als 10.000 Dezimalstellen haben müsste. Im Zusammenhang mit Giugas Vermutung werden die Giuga-Zahlen untersucht.
Lineare Rekursionen
Den kleinen Fermatschen Satz kann man auch in der Form lesen: In der Folge 









das Legendre-Symbol.
Divergenz der Summe der Kehrwerte
Die Reihe der Kehrwerte der Primzahlen ist divergent. Somit gilt:
Das ist gleichbedeutend mit der Aussage, dass die durch 


Primzahltests
Ob eine beliebige natürliche Zahl prim ist, kann mit einem Primzahltest herausgefunden werden. Es gibt mehrere solcher Verfahren, die sich auf besondere Eigenschaften von Primzahlen stützen. In der Praxis wird der Miller-Rabin-Test am häufigsten verwendet, der eine extrem kurze Laufzeit hat, allerdings mit kleiner Wahrscheinlichkeit falsch-positive Ergebnisse liefert. Mit dem AKS-Primzahltest ist es möglich, über die Primalität ohne Gefahr eines Irrtums in polynomieller Laufzeit zu entscheiden. Allerdings ist er in der Praxis deutlich langsamer als der Miller-Rabin-Test.
Primzahlzertifikat
Herauszufinden, ob eine natürliche Zahl prim ist oder nicht, kann sehr aufwändig sein. Zu jeder Primzahl lässt sich aber eine Kette von Behauptungen angeben, die alle unmittelbar nachvollziehbar sind, zusammen die Primalität belegen und deren Gesamtlänge höchstens proportional ist zum Quadrat der Länge der Primzahl. Ein solcher Beleg wird Zertifikat (englisch primality certificate) genannt.
Bei der Zusammengesetztheit (Nichtprimalität) einer Zahl ist der Unterschied zwischen Beleg und Finden eines Belegs noch augenfälliger: Als Beleg genügen zwei Faktoren, deren Produkt die zusammengesetzte Zahl ergibt; das Finden eines echten Teilers kann aber sehr viel Aufwand bedeuten.
Größte bekannte Primzahl
Der Grieche Euklid hat im vierten Jahrhundert vor Christus logisch gefolgert, dass es unendlich viele Primzahlen gibt; diese Aussage wird als Satz von Euklid bezeichnet. Euklid führte einen Widerspruchsbeweis für die Richtigkeit dieses Satzes (Elemente, Buch IX, § 20): Ausgehend von der Annahme, dass es nur endlich viele Primzahlen gibt, lässt sich eine weitere Zahl konstruieren, die eine bisher nicht bekannte Primzahl als Teiler hat oder selbst eine Primzahl ist, was einen Widerspruch zur Annahme darstellt. Somit kann eine endliche Menge niemals alle Primzahlen enthalten, also gibt es unendlich viele. Heute kennt man eine ganze Reihe von Beweisen für den Satz von Euklid.
Der Satz von Euklid besagt, dass es keine größte Primzahl gibt. Es ist jedoch kein Verfahren bekannt, das effizient beliebig große Primzahlen generiert – deshalb gab es stets eine jeweils größte bekannte Primzahl, seitdem sich die Menschen mit Primzahlen befassen. Derzeit (Stand: Dezember 2018) ist es 
Die größte bekannte Primzahl war fast immer eine Mersenne-Primzahl, also von der Form 
Liste der Rekordprimzahlen nach Jahren
| Zahl | Anzahl der Dezimalziffern | Jahr | Entdecker (genutzter Computer) |
|---|---|---|---|
| 217−1 | 6 | 1588 | Cataldi |
| 219−1 | 6 | 1588 | Cataldi |
| 231−1 | 10 | 1772 | Euler |
| (259−1)/179.951 | 13 | 1867 | Landry |
| 2127−1 | 39 | 1876 | Lucas |
| (2148+1)/17 | 44 | 1951 | Ferrier |
| 180·(2127−1)2+1 | 79 | 1951 | Miller & Wheeler (EDSAC1) |
| 2521−1 | 157 | 1952 | Robinson (SWAC) |
| 2607−1 | 183 | 1952 | Robinson (SWAC) |
| 21.279−1 | 386 | 1952 | Robinson (SWAC) |
| 22.203−1 | 664 | 1952 | Robinson (SWAC) |
| 22.281−1 | 687 | 1952 | Robinson (SWAC) |
| 23.217−1 | 969 | 1957 | Riesel (BESK) |
| 24.423−1 | 1.332 | 1961 | Hurwitz (IBM7090) |
| 29.689−1 | 2.917 | 1963 | Gillies (ILLIAC 2) |
| 29.941−1 | 2.993 | 1963 | Gillies (ILLIAC 2) |
| 211.213−1 | 3.376 | 1963 | Gillies (ILLIAC 2) |
| 219.937−1 | 6.002 | 1971 | Tuckerman (IBM360/91) |
| 221.701−1 | 6.533 | 1978 | Noll & Nickel (CDC Cyber 174) |
| 223.209−1 | 6.987 | 1979 | Noll (CDC Cyber 174) |
| 244.497−1 | 13.395 | 1979 | Nelson & Slowinski (Cray 1) |
| 286.243−1 | 25.962 | 1982 | Slowinski (Cray 1) |
| 2132.049−1 | 39.751 | 1983 | Slowinski (Cray X-MP) |
| 2216.091−1 | 65.050 | 1985 | Slowinski (Cray X-MP/24) |
| 391.581·2216.193−1 | 65.087 | 1989 | „Amdahler Sechs“ (Amdahl 1200) |
| 2756.839−1 | 227.832 | 1992 | Slowinski & Gage (Cray 2) |
| 2859.433−1 | 258.716 | 1994 | Slowinski & Gage (Cray C90) |
| 21.257.787−1 | 378.632 | 1996 | Slowinski & Gage (Cray T94) |
| 21.398.269−1 | 420.921 | 1996 | Armengaud, Woltman (GIMPS, Pentium 90 MHz) |
| 22.976.221−1 | 895.932 | 1997 | Spence, Woltman (GIMPS, Pentium 100 MHz) |
| 23.021.377−1 | 909.526 | 1998 | Clarkson, Woltman, Kurowski (GIMPS, Pentium 200 MHz) |
| 26.972.593−1 | 2.098.960 | 1999 | Hajratwala, Woltman, Kurowski (GIMPS, Pentium 350 MHz) |
| 213.466.917−1 | 4.053.946 | 2001 | Cameron, Woltman, Kurowski (GIMPS, Athlon 800 MHz) |
| 220.996.011−1 | 6.320.430 | 2003 | Shafer (GIMPS, Pentium 4 2 GHz) |
| 224.036.583−1 | 7.235.733 | 2004 | Findley (GIMPS, Pentium 4 2,4 GHz) |
| 225.964.951−1 | 7.816.230 | 2005 | Nowak (GIMPS, Pentium 4 2,4 GHz) |
| 230.402.457−1 | 9.152.052 | 2005 | Cooper, Boone (GIMPS, Pentium 4 3 GHz) |
| 232.582.657−1 | 9.808.358 | 2006 | Cooper, Boone (GIMPS, Pentium 4 3 GHz) |
| 243.112.609−1 | 12.978.189 | 2008 | Smith, Woltman, Kurowski et al. (GIMPS, Core 2 Duo 2,4 GHz) |
| 257.885.161−1 | 17.425.170 | 2013 | Cooper, Woltman, Kurowski et al. (GIMPS, Core2 Duo E8400 @ 3,00 GHz) |
| 274.207.281−1 | 22.338.618 | 2016 | Cooper, Woltman, Kurowski et al. (GIMPS, Intel i7-4790 @ 3,60 GHz) |
| 277.232.917−1 | 23.249.425 | 2017 | Jonathan Pace et al. (GIMPS, Intel i5-6600 @ 3,30 GHz) |
| 282.589.933−1 | 24.862.048 | 2018 | Patrick Laroche et al. (GIMPS, Intel i5-4590T @ 2.0 GHz) |
Verteilung und Wachstum
Pi-Funktion und Primzahlsatz
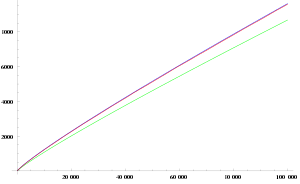
 -Funktion in blau dargestellt. Die Funktion
-Funktion in blau dargestellt. Die Funktion  in grün und der Integrallogarithmus
in grün und der Integrallogarithmus  in rot sind Approximationen der
in rot sind Approximationen der  -Funktion.
-Funktion.Zur Untersuchung der Verteilung der Primzahlen betrachtet man unter anderem die Funktion
,
die die Anzahl der Primzahlen 
.
Diese Funktion und ihr Wachstumsverhalten ist ein beliebter Forschungsgegenstand in der Zahlentheorie. Mit der Zeit wurden einige Näherungsformeln entwickelt und verbessert.
Der Primzahlsatz besagt, dass
gilt, das heißt, dass der Quotient von linker und rechter Seite für 
(siehe Asymptotische Analyse)
Der Dirichletsche Primzahlsatz dagegen schränkt die Betrachtung auf Restklassen ein: Es sei 


höchstens eine Primzahl enthalten, weil alle Folgenglieder durch den größten gemeinsamen Teiler von 






Diese Aussage kann noch in der folgenden Form präzisiert werden: Es gilt:
Dabei ist 



Schranken
Die (bewiesene) Bonsesche Ungleichung garantiert, dass das Quadrat einer Primzahl kleiner ist als das Produkt aller kleineren Primzahlen (ab der fünften Primzahl).
Nach der (unbewiesenen) Andricaschen Vermutung ist die Differenz der Wurzeln der 

Abschätzungen zu Primzahlen und Folgerungen aus dem Primzahlsatz
Im Folgenden sei die Folge der Primzahlen mit 
Abschätzungen
Für Indizes 
- (1a)
- (1b)
für
- (1c)
für
- (1d)
- (1e)
für
Folgerungen aus dem Primzahlsatz
Mit dem Primzahlsatz ergeben sich folgende Resultate:
- (2a)
- (2b)
für
- (2c)
Für jede positive reelle Zahl 

.
- (2d)
Die Menge der aus allen Primzahlen gebildeten Quotienten ist eine dichte Teilmenge der Menge aller positiven reellen Zahlen. D. h.: Für beliebige positive reelle Zahlen 


erfüllt ist.
Primzahllücken
Die Differenz zwischen zwei benachbarten Primzahlen heißt Primzahllücke. Diese Differenz schwankt, und es gibt Primzahllücken beliebiger Größe. Es gibt aber auch Beschränkungen für die Lückengröße in Abhängigkeit von ihrer Lage.
Weitere Aussagen über Primzahl-Verteilungen

- Der Satz von Bertrand sichert die Existenz einer Primzahl zwischen jeder natürlichen Zahl
und ihrem Doppelten
.
- Nach der (unbewiesenen) Legendreschen Vermutung gibt es stets mindestens eine Primzahl zwischen
und
.
Die Legendresche Vermutung stellt eine notwendige Bedingung für die nachfolgende (ebenfalls unbewiesene) Vermutung dar:
- Gegeben sei eine Primzahl
. Die natürlichen Zahlen
bis
seien zeilenweise aufsteigend quadratisch angeordnet wie in der Abbildung für die ersten fünf Primzahlen
und
dargestellt.
- Dann gibt es zu jeder solchen quadratischen Anordnung eine Auswahl von
Primzahlen, so dass sich in jeder Zeile und jeder Spalte genau eine Primzahl befindet.
- Daraus, dass sich in der letzten Zeile einer jeden quadratischen Anordnung mindestens eine Primzahl befinden muss, lässt sich die Legendresche Vermutung folgern.
Generierung von Primzahlen

Einer der ältesten Algorithmen zur Bestimmung von Primzahlen ist das Sieb des Eratosthenes. Bis heute ist kein effizienter Primzahlgenerator bekannt. Es gibt allerdings Formeln, bei denen eine gewisse Wahrscheinlichkeit besteht, dass die erzeugten Zahlen prim sind. Solche Zahlen müssen nachträglich noch auf ihre Primalität getestet werden.
Primzahlen mit identischen Ziffern 1
Seit Beginn des 20. Jahrhunderts beschäftigten sich Experten mit der Frage, unter welchen Bedingungen Zahlen, deren Ziffern ausschließlich Einsen sind (sog. Repunit-Zahlen), Primzahlen sind.
1907 verfasste Henry Ernest Dudeney sein erstes Rätselbuch mit dem Titel The Canterbury Puzzles, in dem er behauptete, dass 11 die einzige Repunit-Primzahl sei. Er konnte zwar nachweisen, dass alle aus 3 bis 18 Ziffern bestehende Repunit-Zahlen keine Primzahlen sind, jedoch gelang ihm dies nicht für Repunit-Zahlen mit mehr als 18 Ziffern.
Nach der Lektüre von Dudeneys Buch bewies 1918 der New Yorker Oscar Hope, dass die 19-stellige Zahl 1.111.111.111.111.111.111 eine Primzahl ist. Später wurde auch die 23-stellige Repunit-Zahl als Primzahl nachgewiesen. Bis 1970 wurden bis zu 373-stellige Repunit-Zahlen untersucht, ohne jedoch eine vierte solche Primzahl zu finden.
Das Problem, ob es mehr als drei oder sogar unendlich viele Repunit-Primzahlen gibt, ist bis heute nicht gelöst.
Weitere spezielle Arten von Primzahlen finden sich in der Kategorie:Primzahl.
Verallgemeinerung
In der Ringtheorie wird das Konzept der Primzahl auf gewisse Elemente eines beliebigen kommutativen unitären Rings verallgemeinert. Die entsprechenden Begriffe sind Primelement und irreduzibles Element.
Die Primzahlen und deren Negative sind dann genau die Primelemente und auch genau die irreduziblen Elemente des Rings der ganzen Zahlen. In faktoriellen Ringen, das sind Ringe mit eindeutiger Primfaktorisierung, fallen die Begriffe Primelement und irreduzibles Element zusammen; im Allgemeinen ist die Menge der Primelemente jedoch nur eine Teilmenge der Menge der irreduziblen Elemente.
Insbesondere im zahlentheoretisch bedeutsamen Fall der Dedekindringe übernehmen Primideale die Rolle der Primzahlen.
Primfaktorzerlegung
Es gilt der Fundamentalsatz der Arithmetik: Jede ganze Zahl größer als 1 lässt sich als Produkt von Primzahlen darstellen, und diese Darstellung ist bis auf die Reihenfolge der Faktoren eindeutig. Man nennt sie die Primfaktoren der Zahl.
Weil sich jede natürliche Zahl größer als 0 durch Multiplikation von Primzahlen darstellen lässt, nehmen die Primzahlen eine besondere atomare Stellung in der Mathematik ein, sie „erzeugen“ gewissermaßen alle anderen natürlichen Zahlen – die Eins als leeres Produkt. Alexander K. Dewdney bezeichnete sie als den Elementen der Chemie weitgehend ähnlich.
Daraus wird auch klar, warum es unzweckmäßig ist, die Eins als Primzahl zu definieren: Sie ist das neutrale Element der Multiplikation und kann somit multiplikativ keine weiteren Zahlen erzeugen. Sie wird für die Darstellung der Zahlen als Produkt von Primfaktoren nicht benötigt. Würde man die 1 zu den Primzahlen zählen, verlöre sich darüber hinaus die Eindeutigkeit der Primfaktorzerlegung, weil man an jede Zerlegung beliebig viele Einsen anhängen kann, ohne den Wert der Zahl zu ändern.
Man hat eine Reihe von Faktorisierungsverfahren entwickelt, um die Primfaktoren von allgemeinen Zahlen oder auch solchen von spezieller Form möglichst schnell zu bestimmen. Man kennt aber bisher keine Methode, um beliebige Zahlen effizient zu faktorisieren, d. h. in einer Zeit, die höchstens polynomiell mit der Länge der gegebenen Zahl wächst. Die Faktorisierungsannahme besagt, dass es eine solche Methode auch nicht gibt.
Anwendung und Auftreten von Primzahlen
Primzahlen in der Natur
Manche Tier- und Pflanzenarten (z. B. bestimmte Zikaden oder Fichten) vermehren sich in Zyklen von Primzahlen (etwa alle 11, 13 oder 17 Jahre) besonders stark, um es Fressfeinden zu erschweren, sich auf das massenhafte Auftreten einzustellen.
Primzahlen in der Informatik
Bei der Informationssicherheit und insbesondere bei der Verschlüsselung von Nachrichten (siehe Kryptographie) spielen Primzahlen eine wichtige Rolle. Sie werden oft in asymmetrischen Kryptosystemen wie etwa Public-Key-Verschlüsselungsverfahren eingesetzt. Wichtige Beispiele sind der Diffie-Hellman-Schlüsselaustausch, das RSA-Kryptosystem, das unter anderem bei OpenPGP zum Einsatz kommt, das Elgamal-Kryptosystem und das Rabin-Kryptosystem. Dabei werden die Schlüssel aus großen, zufällig erzeugten Primzahlen berechnet, die geheim bleiben müssen.
Solche Algorithmen basieren auf Einwegfunktionen, die schnell ausführbar sind, deren Umkehrung aber mit der aktuell bekannten Technologie praktisch unmöglich zu berechnen ist. Neue Informationstechnologien, zum Beispiel Quantencomputer, könnten das aber ändern. Das ungelöste P-NP-Problem steht damit in Zusammenhang.
Warum 1 keine Primzahl ist
Seit hunderten von Jahren diskutieren Mathematiker, ob die Zahl 1 als Primzahl anzusehen ist. Bei dieser Frage handelt es sich nicht um eine mathematische Aussage oder Feststellung, sondern um eine Definition. Definitionen werden intuitiv und/oder pragmatisch begründet; sie sind subjektiv, können aber hinsichtlich ihrer Nützlichkeit durchaus objektiv bewertet werden. Eine gute Definition ist an sich leicht und intuitiv verständlich (d. h. naheliegend) und macht auch die Formulierung von Theoremen leicht und intuitiv verständlich (d. h., sie ist nützlich).
Die Frage, ob 1 eine Primzahl ist, hängt also davon ab, was wir unter dem Begriff Primzahl intuitiv verstehen wollen und wie nützlich die Definition des Begriffs dann für die Formulierung von Theoremen ist.
Der bedeutende Mathematiker Godfrey Harold Hardy bezeichnete zum Beispiel noch im Jahr 1908 die Zahl 1 als Primzahl, aber spätestens im Jahr 1929 nicht mehr. Generell gilt seit dem 20. Jahrhundert unter den allermeisten Mathematikern die Übereinkunft, die Zahl 1 nicht zu den Primzahlen zu zählen.
Das Argument dafür, dass 1 in der Tat eine Primzahl sein sollte, ist:
- Jede Primzahl ist nur durch sich selbst und 1 teilbar.
Anders formuliert: Jede Primzahl hat höchstens zwei Teiler; konkret einen einzigen Teiler für den Fall, dass die Zahl 1 ist, und zwei verschiedene Teiler für den Fall, dass es sich um eine andere Primzahl handelt.
Argumente dafür, dass 1 keine Primzahl sein sollte, sind:
- Jede Primzahl hat genau zwei Teiler (die Zahl 1 und sich selbst), wobei genau zwei konkret bedeutet, dass die Teiler wirklich unterschiedlich sind. Hieran erkennt man, dass das obige Dafür-Argument vielmehr eine unsaubere Wiedergabe dieser Idee entspricht.
- Ein besonders wichtiger Satz in der Mathematik ist die Eindeutigkeit der Primfaktorzerlegung. Wäre
eine Primzahl, so hätte zum Beispiel die zusammengesetzte Zahl
viele verschiedene Primfaktorzerlegungen, zum Beispiel
.
- Damit hätte plötzlich jede Zahl unendlich viele verschiedene Primfaktorzerlegungen und man müsste die Voraussetzungen für diesen wichtigen Satz anders formulieren, damit die Eindeutigkeit wieder gegeben ist. Die Vieldeutigkeit ergibt sich speziell in diesem Zusammenhang daraus, dass die Zahl 1 das neutrale Element der Multiplikation ist, wodurch ihre Nutzung deswegen hierbei unsinnig wird.
- Wenn man zwei Primzahlen miteinander multipliziert, erhält man stets eine zusammengesetzte Zahl, also eine Zahl, die aus mindestens zwei Primfaktoren besteht. Wäre 1 eine Primzahl, könnte man sie zum Beispiel mit einer Primzahl multiplizieren und würde als Produkt wieder eine Primzahl und keine zusammengesetzte Zahl erhalten. Man müsste also die Definition der zusammengesetzten Zahl wesentlich umständlicher fassen.
- Das Sieb des Eratosthenes braucht eine Sonderbehandlung für 1, da man andernfalls als ersten Schritt alle Vielfachen von 1 streichen würde, womit keine einzige andere Zahl mehr übrig bleiben würde außer der 1.
- Für alle Primzahlen
ist die Eulersche Phi-Funktion
. Für
gilt aber
. Der Satz müsste also umformuliert werden und 1 zur Ausnahme machen.
- Für alle Primzahlen
gilt für die Teilerfunktion
. Für
ist aber
. Es gilt auch
. Für
ist aber
. Es wäre also die Zahl 1 auch für diese Funktion(en) eine große Ausnahme.
- Die Definition von Primelementen müsste man umformulieren, wenn 1 eine Primzahl wäre. Die neue Definition wäre komplizierter.
- Es gibt zu jeder Primpotenz einen endlichen Körper, der genau so viele Elemente hat. Wäre 1 eine Primzahl, dann müsste gemäß dieser Aussage der Nullring als Körper aufgefasst werden.
- Die vielfältigen Besonderheiten, die dem Nullring zu eigen sind (z. B. dass er keine echte algebraische Erweiterung zulässt), sind leichter zu würdigen, indem man ihm die Sonderrolle unter den Ringen, die er wirklich einnimmt, auch zuspricht, den Begriff des „Nullkörpers“ nicht bildet und von einem Körper fordert, dass er mindestens zwei Elemente hat, m. a. W., dass sich die neutralen Elemente der beiden Ringoperationen Addition und Multiplikation unterscheiden.
Die Beispiele zeigen gute Gründe, dass man die Zahl 1 aus der Menge der Primzahlen ausschließen sollte.
Siehe auch
Anmerkungen
Literatur
- Peter Bundschuh: Einführung in die Zahlentheorie. 6. Auflage. Springer, Berlin 2008, ISBN 978-3-540-76490-8.
- Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. Beck, München 2004, ISBN 3-406-52320-X.
- Władysław Narkiewicz: The Development of Prime Number Theory. From Euclid to Hardy and Littlewood. Springer, Berlin 2000, ISBN 3-540-66289-8.
- Paulo Ribenboim: The New Book of Prime Number Records. Springer, New York 1996, ISBN 0-387-94457-5.
- Robert E. Dressler, Louis Pigno, Robert Young: Sums of squares of primes. In: Nordisk Mat. Tidskr. Band 24, 1976, S. 39–40 (MR0419352).
- Hans Rademacher, Otto Toeplitz: Von Zahlen und Figuren. Proben mathematischen Denkens für Liebhaber der Mathematik (= Heidelberger Taschenbücher. Band 50). Springer Verlag, Berlin (u. a.) 1968 (MR0252141).
- J. B. Rosser: The n-th prime is greater than n log n. In: Proc. London Math. Soc. Band 45, 1939, S. 21–44.
- J. Barkley Rosser, L. Schoenfeld: Approximate formulas for some functions of prime numbers. In: Illinois J. Math. Band 6, 1962, S. 64–94 (projecteuclid.org [PDF]). MR0137689
- József Sándor, Dragoslav S. Mitrinović, Borislav Crstici: Handbook of Number Theory. 2. Auflage. Band I. Springer-Verlag, Dordrecht (NL) 2006, ISBN 1-4020-4215-9 (MR2186914).
- Wacław Sierpiński: Elementary Theory of Numbers. Edited and with a preface by Andrzej Schinzel (= North-Holland Mathematical Library. Band 31). 2. überarbeitete und erweiterte Auflage. North-Holland (u. a.), Amsterdam (u. a.) 1988, ISBN 0-444-86662-0 (MR0930670).
- Rebecca Waldecker, Lasse Rempe-Gillen: Primzahltests für Einsteiger: Zahlentheorie–Algorithmik–Kryptographie. 2. Auflage. Springer Spektrum, Wiesbaden 2016, ISBN 978-3-658-11216-5, doi:10.1007/978-3-658-11217-2.
Weblinks
- The Prime Pages (englisch)
- Die Primzahlenseite
- Eric W. Weisstein: Rosser’s Theorem. In: MathWorld (englisch).
- Gesammelte Sätze und interessante Eigenschaften über Primzahlen. (PDF; 162 Seiten) Mathematik alpha (deutsch).
Einzelnachweise
This article uses material from the Wikipedia Deutsch article Primzahl, which is released under the Creative Commons Attribution-ShareAlike 3.0 license ("CC BY-SA 3.0"); additional terms may apply (view authors). Abrufstatistik · Autoren Der Inhalt ist verfügbar unter CC BY-SA 4.0, sofern nicht anders angegeben. Images, videos and audio are available under their respective licenses.
®Wikipedia is a registered trademark of the Wiki Foundation, Inc. Wiki Deutsch (DUHOCTRUNGQUOC.VN) is an independent company and has no affiliation with Wiki Foundation.































