Partially Ordered Set
All definitions tacitly require the homogeneous relation R be transitive: for all a , b , c , if a R b and b R c then a R c .
| Transitive binary relations | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In mathematics, especially order theory, a partial order on a set is an arrangement such that, for certain pairs of elements, one precedes the other. The word partial is used to indicate that not every pair of elements needs to be comparable; that is, there may be pairs for which neither element precedes the other. Partial orders thus generalize total orders, in which every pair is comparable.

Formally, a partial order is a homogeneous binary relation that is reflexive, antisymmetric, and transitive. A partially ordered set (poset for short) is an ordered pair of a set (called the ground set of ) and a partial order on . When the meaning is clear from context and there is no ambiguity about the partial order, the set itself is sometimes called a poset.
Partial order relations
The term partial order usually refers to the reflexive partial order relations, referred to in this article as non-strict partial orders. However some authors use the term for the other common type of partial order relations, the irreflexive partial order relations, also called strict partial orders. Strict and non-strict partial orders can be put into a one-to-one correspondence, so for every strict partial order there is a unique corresponding non-strict partial order, and vice versa.
Partial orders
A reflexive, weak, or non-strict partial order, commonly referred to simply as a partial order, is a homogeneous relation ≤ on a set 

- Reflexivity:
, i.e. every element is related to itself.
- Antisymmetry: if
and
then
, i.e. no two distinct elements precede each other.
- Transitivity: if
and
then
.
A non-strict partial order is also known as an antisymmetric preorder.
Strict partial orders
An irreflexive, strong, or strict partial order is a homogeneous relation < on a set 

- Irreflexivity: not
, i.e. no element is related to itself (also called anti-reflexive).
- Asymmetry: if
then not
.
- Transitivity: if
and
then
.
Irreflexivity and transitivity together imply asymmetry. Also, asymmetry implies irreflexivity. In other words, a transitive relation is asymmetric if and only if it is irreflexive. So the definition is the same if it omits either irreflexivity or asymmetry (but not both).
A strict partial order is also known as an asymmetric strict preorder.
Correspondence of strict and non-strict partial order relations
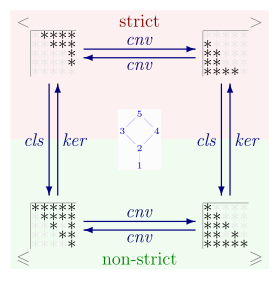
 so row 3, column 4 of the bottom left matrix is empty.
so row 3, column 4 of the bottom left matrix is empty.Strict and non-strict partial orders on a set 










 is the reflexive closure given by:
is the reflexive closure given by: 
Dual orders
The dual (or opposite) 





Notation
Given a set 

















The term ordered set is sometimes used as a shorthand for partially ordered set, as long as it is clear from the context that no other kind of order is meant. In particular, totally ordered sets can also be referred to as "ordered sets", especially in areas where these structures are more common than posets. Some authors use different symbols than 


When referring to partial orders, 







Alternative definitions
Another way of defining a partial order, found in computer science, is via a notion of comparison. Specifically, given 

Wallis defines a more general notion of a partial order relation as any homogeneous relation that is transitive and antisymmetric. This includes both reflexive and irreflexive partial orders as subtypes.
A finite poset can be visualized through its Hasse diagram. Specifically, taking a strict partial order relation 


Examples

Standard examples of posets arising in mathematics include:
- The real numbers, or in general any totally ordered set, ordered by the standard less-than-or-equal relation ≤, is a partial order.
- On the real numbers
, the usual less than relation < is a strict partial order. The same is also true of the usual greater than relation > on
.
- By definition, every strict weak order is a strict partial order.
- The set of subsets of a given set (its power set) ordered by inclusion (see Fig. 1). Similarly, the set of sequences ordered by subsequence, and the set of strings ordered by substring.
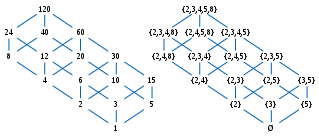
- The set of natural numbers equipped with the relation of divisibility. (see Fig. 3 and Fig. 6)
- The vertex set of a directed acyclic graph ordered by reachability.
- The set of subspaces of a vector space ordered by inclusion.
- For a partially ordered set P, the sequence space containing all sequences of elements from P, where sequence a precedes sequence b if every item in a precedes the corresponding item in b. Formally,
if and only if
for all
; that is, a componentwise order.
- For a set X and a partially ordered set P, the function space containing all functions from X to P, where f ≤ g if and only if f(x) ≤ g(x) for all
- A fence, a partially ordered set defined by an alternating sequence of order relations a < b > c < d ...
- The set of events in special relativity and, in most cases, general relativity, where for two events X and Y, X ≤ Y if and only if Y is in the future light cone of X. An event Y can be causally affected by X only if X ≤ Y.
One familiar example of a partially ordered set is a collection of people ordered by genealogical descendancy. Some pairs of people bear the descendant-ancestor relationship, but other pairs of people are incomparable, with neither being a descendant of the other.
Orders on the Cartesian product of partially ordered sets


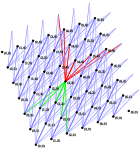
 Elements covered by (3, 3) and covering (3, 3) are highlighted in green and red, respectively.
Elements covered by (3, 3) and covering (3, 3) are highlighted in green and red, respectively.In order of increasing strength, i.e., decreasing sets of pairs, three of the possible partial orders on the Cartesian product of two partially ordered sets are (see Fig. 4):
- the lexicographical order: (a, b) ≤ (c, d) if a < c or (a = c and b ≤ d);
- the product order: (a, b) ≤ (c, d) if a ≤ c and b ≤ d;
- the reflexive closure of the direct product of the corresponding strict orders: (a, b) ≤ (c, d) if (a < c and b < d) or (a = c and b = d).
All three can similarly be defined for the Cartesian product of more than two sets.
Applied to ordered vector spaces over the same field, the result is in each case also an ordered vector space.
See also orders on the Cartesian product of totally ordered sets.
Sums of partially ordered sets
Another way to combine two (disjoint) posets is the ordinal sum (or linear sum), Z = X ⊕ Y, defined on the union of the underlying sets X and Y by the order a ≤Z b if and only if:
- a, b ∈ X with a ≤X b, or
- a, b ∈ Y with a ≤Y b, or
- a ∈ X and b ∈ Y.
If two posets are well-ordered, then so is their ordinal sum.
Series-parallel partial orders are formed from the ordinal sum operation (in this context called series composition) and another operation called parallel composition. Parallel composition is the disjoint union of two partially ordered sets, with no order relation between elements of one set and elements of the other set.
Derived notions
The examples use the poset 

- a is related to b when a ≤ b. This does not imply that b is also related to a, because the relation need not be symmetric. For example,
is related to
but not the reverse.
- a and b are comparable if a ≤ b or b ≤ a. Otherwise they are incomparable. For example,
and
are comparable, while
and
are not.
- A total order or linear order is a partial order under which every pair of elements is comparable, i.e. trichotomy holds. For example, the natural numbers with their standard order.
- A chain is a subset of a poset that is a totally ordered set. For example,
is a chain.
- An antichain is a subset of a poset in which no two distinct elements are comparable. For example, the set of singletons
- An element a is said to be strictly less than an element b, if a ≤ b and
For example,
is strictly less than
- An element a is said to be covered by another element b, written a ⋖ b (or a <: b), if a is strictly less than b and no third element c fits between them; formally: if both a ≤ b and
are true, and a ≤ c ≤ b is false for each c with
Using the strict order <, the relation a ⋖ b can be equivalently rephrased as "a < b but not a < c < b for any c". For example,
is covered by
but is not covered by
Extrema

There are several notions of "greatest" and "least" element in a poset 
- Greatest element and least element: An element
is a greatest element if
for every element
An element
is a least element if
for every element
A poset can only have one greatest or least element. In our running example, the set
is the greatest element, and
is the least.
- Maximal elements and minimal elements: An element
is a maximal element if there is no element
such that
Similarly, an element
is a minimal element if there is no element
such that
If a poset has a greatest element, it must be the unique maximal element, but otherwise there can be more than one maximal element, and similarly for least elements and minimal elements. In our running example,
and
are the maximal and minimal elements. Removing these, there are 3 maximal elements and 3 minimal elements (see Fig. 5).
- Upper and lower bounds: For a subset A of P, an element x in P is an upper bound of A if a ≤ x, for each element a in A. In particular, x need not be in A to be an upper bound of A. Similarly, an element x in P is a lower bound of A if a ≥ x, for each element a in A. A greatest element of P is an upper bound of P itself, and a least element is a lower bound of P. In our example, the set
is an upper bound for the collection of elements

As another example, consider the positive integers, ordered by divisibility: 1 is a least element, as it divides all other elements; on the other hand this poset does not have a greatest element. This partially ordered set does not even have any maximal elements, since any g divides for instance 2g, which is distinct from it, so g is not maximal. If the number 1 is excluded, while keeping divisibility as ordering on the elements greater than 1, then the resulting poset does not have a least element, but any prime number is a minimal element for it. In this poset, 60 is an upper bound (though not a least upper bound) of the subset 
Mappings between partially ordered sets
 v) map.
v) map.Given two partially ordered sets (S, ≤) and (T, ≼), a function 

















For example, a mapping 





Number of partial orders
Sequence A001035 in OEIS gives the number of partial orders on a set of n labeled elements:
| Elements | Any | Transitive | Reflexive | Symmetric | Preorder | Partial order | Total preorder | Total order | Equivalence relation |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 1 |
| 2 | 16 | 13 | 4 | 8 | 4 | 3 | 3 | 2 | 2 |
| 3 | 512 | 171 | 64 | 64 | 29 | 19 | 13 | 6 | 5 |
| 4 | 65,536 | 3,994 | 4,096 | 1,024 | 355 | 219 | 75 | 24 | 15 |
| n | 2n2 | 2n(n−1) | 2n(n+1)/2 | ∑n k=0 k!S(n, k) | n! | ∑n k=0 S(n, k) | |||
| OEIS | A002416 | A006905 | A053763 | A006125 | A000798 | A001035 | A000670 | A000142 | A000110 |
Note that S(n, k) refers to Stirling numbers of the second kind.
The number of strict partial orders is the same as that of partial orders.
If the count is made only up to isomorphism, the sequence 1, 1, 2, 5, 16, 63, 318, ... (sequence A000112 in the OEIS) is obtained.
Linear extension
A partial order 






In computer science, algorithms for finding linear extensions of partial orders (represented as the reachability orders of directed acyclic graphs) are called topological sorting.
In category theory
Every poset (and every preordered set) may be considered as a category where, for objects 




Posets are equivalent to one another if and only if they are isomorphic. In a poset, the smallest element, if it exists, is an initial object, and the largest element, if it exists, is a terminal object. Also, every preordered set is equivalent to a poset. Finally, every subcategory of a poset is isomorphism-closed. In differential topology, homology theory (HT) is used for classifying equivalent smooth manifolds M, related to the geometrical shapes of M. In homology theory is given an axiomatic HT approach, especially to singular homology.[clarification needed] The HT members are algebraic invariants under diffeomorphisms. The axiomatic HT category is taken in G. Kalmbach from the book Eilenberg–Steenrod (see the references) in order to show that the set theoretical topological concept for the HT definition can be extended to partial ordered sets P. Important are chains and filters in P (replacing shapes of M) for defining HT classifications, available for many P applications not related to set theory.
Partial orders in topological spaces
If 







Intervals
A convex set in a poset P is a subset I of P with the property that, for any x and y in I and any z in P, if x ≤ z ≤ y, then z is also in I. This definition generalizes the definition of intervals of real numbers. When there is possible confusion with convex sets of geometry, one uses order-convex instead of "convex".
A convex sublattice of a lattice L is a sublattice of L that is also a convex set of L. Every nonempty convex sublattice can be uniquely represented as the intersection of a filter and an ideal of L.
An interval in a poset P is a subset that can be defined with interval notation:
- For a ≤ b, the closed interval [a, b] is the set of elements x satisfying a ≤ x ≤ b (that is, a ≤ x and x ≤ b). It contains at least the elements a and b.
- Using the corresponding strict relation "<", the open interval (a, b) is the set of elements x satisfying a < x < b (i.e. a < x and x < b). An open interval may be empty even if a < b. For example, the open interval (0, 1) on the integers is empty since there is no integer x such that 0 < x < 1.
- The half-open intervals [a, b) and (a, b] are defined similarly.
Whenever a ≤ b does not hold, all these intervals are empty. Every interval is a convex set, but the converse does not hold; for example, in the poset of divisors of 120, ordered by divisibility (see Fig. 7b), the set {1, 2, 4, 5, 8} is convex, but not an interval.
An interval I is bounded if there exist elements 
A poset is called locally finite if every bounded interval is finite. For example, the integers are locally finite under their natural ordering. The lexicographical order on the cartesian product 

This concept of an interval in a partial order should not be confused with the particular class of partial orders known as the interval orders.
See also
- Antimatroid, a formalization of orderings on a set that allows more general families of orderings than posets
- Causal set, a poset-based approach to quantum gravity
- Comparability graph – Graph linking pairs of comparable elements in a partial order
- Complete partial order – term used in mathematical order theory
- Directed set – Mathematical ordering with upper bounds
- Graded poset – partially ordered set equipped with a rank function, sometimes called a ranked poset
- Incidence algebra – associative algebra used in combinatorics, a branch of mathematics
- Lattice – Set whose pairs have minima and maxima
- Locally finite poset – Mathematics
- Möbius function on posets – associative algebra used in combinatorics, a branch of mathematics
- Nested set collection
- Order polytope
- Ordered field – Algebraic object with an ordered structure
- Ordered group – Group with a compatible partial order
- Ordered vector space – Vector space with a partial order
- Poset topology, a kind of topological space that can be defined from any poset
- Scott continuity – continuity of a function between two partial orders.
- Semilattice – Partial order with joins
- Semiorder – Numerical ordering with a margin of error
- Szpilrajn extension theorem – every partial order is contained in some total order.
- Stochastic dominance – Partial order between random variables
- Strict weak ordering – strict partial order "<" in which the relation "neither a < b nor b < a" is transitive.
- Total order – Order whose elements are all comparable
- Tree – Data structure of set inclusion
- Zorn's lemma – Mathematical proposition equivalent to the axiom of choice
Notes
Citations
References
- Davey, B. A.; Priestley, H. A. (2002). Introduction to Lattices and Order (2nd ed.). New York: Cambridge University Press. ISBN 978-0-521-78451-1.
- Deshpande, Jayant V. (1968). "On Continuity of a Partial Order". Proceedings of the American Mathematical Society. 19 (2): 383–386. doi:10.1090/S0002-9939-1968-0236071-7.
- Schmidt, Gunther (2010). Relational Mathematics. Encyclopedia of Mathematics and its Applications. Vol. 132. Cambridge University Press. ISBN 978-0-521-76268-7.
- Bernd Schröder (11 May 2016). Ordered Sets: An Introduction with Connections from Combinatorics to Topology. Birkhäuser. ISBN 978-3-319-29788-0.
- Stanley, Richard P. (1997). Enumerative Combinatorics 1. Cambridge Studies in Advanced Mathematics. Vol. 49. Cambridge University Press. ISBN 0-521-66351-2.
- Eilenberg, S. (2016). Foundations of Algebraic Topology. Princeton University Press.
- Kalmbach, G. (1976). "Extension of Homology Theory to Partially Ordered Sets". J. Reine Angew. Math. 280: 134–156.
External links

This article uses material from the Wikipedia English article Partially ordered set, which is released under the Creative Commons Attribution-ShareAlike 3.0 license ("CC BY-SA 3.0"); additional terms may apply (view authors). Content is available under CC BY-SA 4.0 unless otherwise noted. Images, videos and audio are available under their respective licenses.
®Wikipedia is a registered trademark of the Wiki Foundation, Inc. Wiki English (DUHOCTRUNGQUOC.VN) is an independent company and has no affiliation with Wiki Foundation.