Subset

It is possible for A and B to be equal; if they are unequal, then A is a proper subset of B. The relationship of one set being a subset of another is called inclusion (or sometimes containment). A is a subset of B may also be expressed as B includes (or contains) A or A is included (or contained) in B. A k-subset is a subset with k elements.

The subset relation defines a partial order on sets. In fact, the subsets of a given set form a Boolean algebra under the subset relation, in which the join and meet are given by intersection and union, and the subset relation itself is the Boolean inclusion relation.

If A and B are sets and every element of A is also an element of B, then:

• A is a subset of B, denoted by ${\displaystyle A\subseteq B}$ , or equivalently,
• B is a superset of A, denoted by ${\displaystyle B\supseteq A.}$ 

If A is a subset of B, but A is not equal to B (i.e. there exists at least one element of B which is not an element of A), then:

• A is a proper (or strict) subset of B, denoted by ${\displaystyle A\subsetneq B}$ , or equivalently,
• B is a proper (or strict) superset of A, denoted by ${\displaystyle B\supsetneq A.}$ 

The empty set, written ${\displaystyle \{\}}$  or ${\displaystyle \varnothing ,}$  is a subset of any set X and a proper subset of any set except itself, the inclusion relation ${\displaystyle \subseteq }$  is a partial order on the set ${\displaystyle {\mathcal {P}}(S)}$  (the power set of S—the set of all subsets of S) defined by ${\displaystyle A\leq B\iff A\subseteq B}$ . We may also partially order ${\displaystyle {\mathcal {P}}(S)}$  by reverse set inclusion by defining ${\displaystyle A\leq B{\text{ if and only if }}B\subseteq A.}$ 

When quantified, ${\displaystyle A\subseteq B}$  is represented as ${\displaystyle \forall x\left(x\in A\implies x\in B\right).}$ 

We can prove the statement ${\displaystyle A\subseteq B}$  by applying a proof technique known as the element argument:

Let sets A and B be given. To prove that ${\displaystyle A\subseteq B,}$ 

1. suppose that a is a particular but arbitrarily chosen element of A
2. show that a is an element of B.

The validity of this technique can be seen as a consequence of universal generalization: the technique shows ${\displaystyle c\in A\implies c\in B}$  for an arbitrarily chosen element c. Universal generalisation then implies ${\displaystyle \forall x\left(x\in A\implies x\in B\right),}$  which is equivalent to ${\displaystyle A\subseteq B,}$  as stated above.

The set of all subsets of ${\displaystyle A}$  is called its powerset, and is denoted by ${\displaystyle {\mathcal {P}}(A)}$ . The set of all ${\displaystyle k}$ -subsets of ${\displaystyle A}$  is denoted by ${\displaystyle {\tbinom {A}{k}}}$ , in analogue with the notation for binomial coefficients, which count the number of ${\displaystyle k}$ -subsets of an ${\displaystyle n}$ -element set. In set theory, the notation ${\displaystyle [A]^{k}}$  is also common, especially when ${\displaystyle k}$  is a transfinite cardinal number.

• A set A is a subset of B if and only if their intersection is equal to A.

Formally:
${\displaystyle A\subseteq B{\text{ if and only if }}A\cap B=A.}$ 

• A set A is a subset of B if and only if their union is equal to B.

Formally:
${\displaystyle A\subseteq B{\text{ if and only if }}A\cup B=B.}$ 

• A finite set A is a subset of B, if and only if the cardinality of their intersection is equal to the cardinality of A.

Formally:
${\displaystyle A\subseteq B{\text{ if and only if }}|A\cap B|=|A|.}$ 

Some authors use the symbols ${\displaystyle \subset }$  and ${\displaystyle \supset }$  to indicate subset and superset respectively; that is, with the same meaning as and instead of the symbols ${\displaystyle \subseteq }$  and ${\displaystyle \supseteq .}$  For example, for these authors, it is true of every set A that ${\displaystyle A\subset A.}$  (a reflexive relation).

Other authors prefer to use the symbols ${\displaystyle \subset }$  and ${\displaystyle \supset }$  to indicate proper (also called strict) subset and proper superset respectively; that is, with the same meaning as and instead of the symbols ${\displaystyle \subsetneq }$  and ${\displaystyle \supsetneq .}$  This usage makes ${\displaystyle \subseteq }$  and ${\displaystyle \subset }$  analogous to the inequality symbols ${\displaystyle \leq }$  and ${\displaystyle <.}$  For example, if ${\displaystyle x\leq y,}$  then x may or may not equal y, but if ${\displaystyle x$  then x definitely does not equal y, and is less than y (an irreflexive relation). Similarly, using the convention that ${\displaystyle \subset }$  is proper subset, if ${\displaystyle A\subseteq B,}$  then A may or may not equal B, but if ${\displaystyle A\subset B,}$  then A definitely does not equal B.

 

• The set A = {1, 2} is a proper subset of B = {1, 2, 3}, thus both expressions ${\displaystyle A\subseteq B}$  and ${\displaystyle A\subsetneq B}$  are true.
• The set D = {1, 2, 3} is a subset (but not a proper subset) of E = {1, 2, 3}, thus ${\displaystyle D\subseteq E}$  is true, and ${\displaystyle D\subsetneq E}$  is not true (false).
• Any set is a subset of itself, but not a proper subset. (${\displaystyle X\subseteq X}$  is true, and ${\displaystyle X\subsetneq X}$  is false for any set X.)
• The set {x: x is a prime number greater than 10} is a proper subset of {x: x is an odd number greater than 10}
• The set of natural numbers is a proper subset of the set of rational numbers; likewise, the set of points in a line segment is a proper subset of the set of points in a line. These are two examples in which both the subset and the whole set are infinite, and the subset has the same cardinality (the concept that corresponds to size, that is, the number of elements, of a finite set) as the whole; such cases can run counter to one's initial intuition.
• The set of rational numbers is a proper subset of the set of real numbers. In this example, both sets are infinite, but the latter set has a larger cardinality (or power) than the former set.

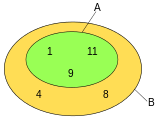
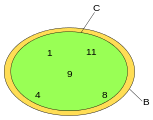
Another example in an Euler diagram:

•  
  A is a proper subset of B.
•  
  C is a subset but not a proper subset of B.

 

Inclusion is the canonical partial order, in the sense that every partially ordered set ${\displaystyle (X,\preceq )}$  is isomorphic to some collection of sets ordered by inclusion. The ordinal numbers are a simple example: if each ordinal n is identified with the set ${\displaystyle [n]}$  of all ordinals less than or equal to n, then ${\displaystyle a\leq b}$  if and only if ${\displaystyle [a]\subseteq [b].}$ 

For the power set ${\displaystyle \operatorname {\mathcal {P}} (S)}$  of a set S, the inclusion partial order is—up to an order isomorphism—the Cartesian product of ${\displaystyle k=|S|}$  (the cardinality of S) copies of the partial order on ${\displaystyle \{0,1\}}$  for which ${\displaystyle 0<1.}$  This can be illustrated by enumerating ${\displaystyle S=\left\{s_{1},s_{2},\ldots ,s_{k}\right\},}$ , and associating with each subset ${\displaystyle T\subseteq S}$  (i.e., each element of ${\displaystyle 2^{S}}$ ) the k-tuple from ${\displaystyle \{0,1\}^{k},}$  of which the ith coordinate is 1 if and only if ${\displaystyle s_{i}}$  is a member of T.

• Convex subset – In geometry, set whose intersection with every line is a single line segmentPages displaying short descriptions of redirect targets
• Inclusion order – Partial order that arises as the subset-inclusion relation on some collection of objects
• Region – Connected open subset of a topological spacePages displaying short descriptions of redirect targets
• Subset sum problem – Decision problem in computer science
• Subsumptive containment – System of elements that are subordinated to each other
• Total subset – Subset T of a topological vector space X where the linear span of T is a dense subset of X
• Mereology – Study of parts and the wholes they form