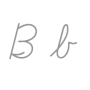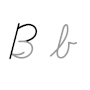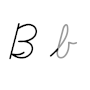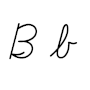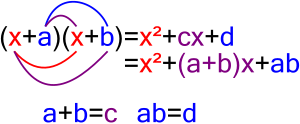B

Wiktionary میدیای پەیوەندیدار بە B لە ویکیمیدیا کۆمنز The dictionary definition of b at Wiktionary  Giles, Peter (1911). "B" . Encyclopædia Britannica. Vol...

کە ئەگەر a و b دوو ئاڕاستەبڕ (یا ھێڵ) بن کە لە سەری O گۆشەی A پێک بێنن، ھاوکێشەی a 2 + b 2 − 2 a b C o s A = c 2 {\displaystyle a^{2}+b^{2}-2abCos{A}=c^{2}}...

a + bi کە a و b ژمارەی ڕاستین و i یەکەی خەیاڵییە بەم شێوەیە کە i 2 = − 1 {\displaystyle i^{2}=-1} . I m z = b {\displaystyle I_{m}z=b} R e z = a {\displaystyle...

لە: A ∪ B = B ∪ A. A ∪ (B ∪ C) = (A ∪ B) ∪ C. A ⊆ (A ∪ B). A ∪ A = A. A ∪ U = U. A ∪ ∅ = A. A ⊆ B ئەگەر و تەنھا ئەگەر A ∪ B = B. یەکتربڕینی A و B، بەم شێوە...

b {\displaystyle b} دوو بەھای بوارەکەی بن ئەوا تەواوکاریی سنووردار بۆ فانکشنی f {\displaystyle f} لە نێوان a {\displaystyle a} و b {\displaystyle b}...

و b = [ b 1 , b 2 , ⋯ , b n ] {\displaystyle \mathbf {b} =[b_{1},b_{2},\cdots ,b_{n}]\!} بەم شێوە پێناسە دەکرێت: a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 +...

سێگۆشە دەبێتە کۆی درێژیی ھەر سێ لاکەی، واتە: P=a+b+c{\displaystyle P=a+b+c}؛ P چێوەیە؛ ھەر کام لە a و b و c ژمارەیەکن نیشاندەری درێژی یەکێ لە لاکان. ئەگەر...

گرووپی B ی جامی نەتەوەکانی ئەورووپا ٢٠٢٠ لە ١٢ حوزەیرانی ٢٠٢١ یارییەکانی گەڕی یەکەمی بەڕێوەچوو. ئەم گرووپە لە ھەریەکە لە ھەڵبژاردەکانی ڕووسیا و دانیمارکی...

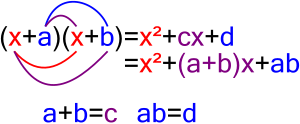(a-b)^{2}=a^{2}-2ab+b^{2}\,\!} ( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 {\displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\,\!} ( a − b ) 3 = a 3 − 3 a 2 b + 3 a b 2...

B-Tree یان درەختی-بی لە زانستی کۆمپیوتەردا پێکھاتەیەکی درەختیی داتایە کەوا داتا بە ڕیزکراوی ئەھێڵێتەوە، ڕێگاش ئەدات 'گەڕان' بکرێ تیایدا، بەدەستخستنی بەسەرە،...

نیشاندەدرێن. ڕستەی دوو کۆمەڵی A و B پێکەوە بەرانبەرن واتە A و B ڕێک ھەمان ئەندامانیان ھەیە (ھەر ئەندامی A ئەندامی Bیە و بەپێچەوانەش). پێویستە ھەرکام لە...

a} و b {\displaystyle b} و c {\displaystyle c} درێژی لایەکانی سێگۆشەیەک بن ئەوا: c 2 = a 2 + b 2 − 2 a b cos ⁡ ( γ ) , {\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos(\gamma...

دەنووسرێت، بەم شێوە: a x 2 + b x + c = 0 {\displaystyle ax^{2}+bx+c=0\,} لێرەدا x {\displaystyle x\,} گۆڕەک، a , b , c {\displaystyle a,b,c\,} ژمارەی نەگۆڕ و ڕاستەقینەن،...

4\}} و B = { a , b } {\displaystyle B=\{a,b\}} لێکدانی دێکارتی دوو کۆمەڵی A {\displaystyle A} و B {\displaystyle B} ، بریتییە لە b ( 1 , b ) ( 2 , b ) (...

ستانداردکردن (ISO) و ڕۆژژمێری گریگۆری، چوارشەممە سێیەم ڕۆژی هەفتەیە. ناوی ڕۆژەکە لە وشەکانی چوار و شەممە هاتووە. داڕێژە:Commonscat-b داڕێژە:چوارشەممە...

دووپاتەبووە. ئەگەر c جار b یەکسان بێت لەگەڵ a، ئەوە دەنووسرێت: c × b = a {\displaystyle c\times b=a\,} وە ئەگەر b سیفر نەبێت، ئەوکات a دابەش بە b دەبێتە c و بەم...

, b ] {\displaystyle [a,b]} و لە ماوەی ( a , b ) {\displaystyle (a,b)} توانای گرتەی ھەبێت، ئەوا خاڵێک وەکوو c ∈ ( a , b ) {\displaystyle c\in (a,b)} ھەیە...

a + b + c ) ( − a + b + c ) ( a − b + c ) ( a + b − c ) {\displaystyle A={\frac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}} A = 1 4 2 ( a 2 b 2 +...

a ± b ) = cos ⁡ a . cos ⁡ b ∓ sin ⁡ a . sin ⁡ b {\displaystyle \cos(a\pm b)=\cos a.\cos b\mp \sin a.\sin b\,} سەرجەم و جیاوازی ساین: sin ⁡ ( a ± b ) =...

A\subseteq B}، یان بە شێوەی ھاوەسەنگ: B سەرکۆمەڵــێکی Aیە (یان B داگری Aیە)، وە بەم جۆرە دیاریدەکرێت: B⊇A.{\displaystyle B\supseteq A.} ئەگەر A ژێرکۆمەڵی B بێت،...