Formula Lui Euler

${\displaystyle e^{ix}=\cos(x)+i\sin(x)\!}$

unde

• ${\displaystyle e\,}$ este baza logaritmului natural
• ${\displaystyle i\,}$ este unitatea imaginară
• ${\displaystyle \mathrm {cos} }$ și ${\displaystyle \mathrm {sin} }$ sunt funcțiile trigonometrice cu argumentul exprimat în radiani.

Richard Feynman a numit formula lui Euler "bijuteria noastră" și "cea mai remarcabilă formulă din matematică".

Pentru cazul particular x = π este valabilă identitatea:

${\displaystyle e^{i\pi }+1=0\,}$

care combină într-o formulă simplă cele cinci numere fundamentale i, π, e,1 și 0.

Roger Cotes în 1714 dădea un argument geometric intuitiv folosind cercul trigonometric și factorizarea complexă a unei sume de pătrate ${\displaystyle a^{2}+b^{2}=(a+ib)(a+ib)}$  rezultată prin teorema lui Pitagora pentru formula lui Euler sub formă logaritmică:

${\displaystyle \ln(\cos(x)+i\sin(x))=ix\ }$ 

(unde "ln" înseamnă logaritm natural, adică logaritm în bază e).

Prima demonstrație a egalității în forma ei actuală datează din 1748, Euler bazându-și demonstrația pe egalitatea seriilor infinite din ambele părți ale egalității. Roger Cotes, prin argumentul său geometric, intuia oarecum reprezentarea geometrică a formulei bazată pe reprezentarea numerelor complexe ca puncte din planul complex, apărută ulterior abia după 50 de ani.

Euler considera firesc să prezinte studenților numerele complexe mult mai devreme decât se practică astăzi în predarea algebrei. În manualul său Elemente de Algebră el introduce aceste numere aproape de la început și le folosește de-a lungul întregii lucrări.

 

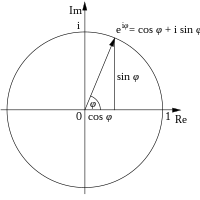
Formula lui Euler, numită astfel după Leonhard Euler, este o formulă matematică din analiza complexă care arată o relație strânsă între funcțiile trigonometrice și funcția exponențială complexă. (Identitatea lui Euler este un caz particular al formulei lui Euler.)

Această formulă poate fi interpretată spunând că funcția e^ix trasează cercul unitate din planul numerelor complexe când x ia valori reale. Aici, x este unghiul dintre o dreaptă care leagă originea cu un punct pe cercul unitate și axa reală pozitivă, măsurată în sens trigonometric în radiani. Formula este validă doar dacă sin și cos au argumentele exprimate în radiani, nu în grade.

Demonstrația originală se bazează pe dezvoltările în serie Taylor ale funcțiilor exponențială e^z (cu z complex), sin x și cos x pentru numere reale x. De fapt, aceeași demonstrație arată că formula lui Euler este valabilă și pentru toate numerele complexe z.

Formula lui Euler poate fi folosită pentru a reprezenta numerele complexe în coordonate polare. Orice număr complex z = x + iy poate fi scris sub forma

${\displaystyle z=x+iy=|z|(\cos \phi +i\sin \phi )=|z|e^{i\phi }\,}$ 
${\displaystyle {\bar {z}}=x-iy=|z|(\cos \phi -i\sin \phi )=|z|e^{-i\phi }\,}$ 

unde

${\displaystyle x=\mathrm {Re} \{z\}\,}$  partea reală
${\displaystyle y=\mathrm {Im} \{z\}\,}$  partea imaginară
${\displaystyle |z|={\sqrt {x^{2}+y^{2}}}}$  modulul lui z

și ${\displaystyle \phi \,}$  este argumentul lui z— unghiul între axa x și vectorul z măsurat în sens trigonometric și în radiani — definit până la 2π.

Acum, luând această formulă derivată, se poate folosi formula lui Euler pentru a defini logaritmul unui număr complex. Pentru a face asta, se folosește și faptul că

${\displaystyle a=e^{\ln(a)}\,}$ 

și

${\displaystyle e^{a}e^{b}=e^{a+b}\,}$ 

ambele valabile pentru numerele complexe a și b.

De aceea se poate scrie:

${\displaystyle z=|z|e^{i\phi }=e^{\ln |z|}e^{i\phi }=e^{\ln |z|+i\phi }\,}$ 

pentru orice ${\displaystyle z\neq 0}$ . Scoțând logaritm din ambele părți, rezultă:

${\displaystyle \ln z=\ln |z|+i\phi .\,}$ 

și aceasta se poate folosi ca definiția logaritmului complex.

În fine, identitatea exponențială

${\displaystyle (e^{a})^{k}=e^{ak},\,}$ 

care este valabilă pentru orice întreg k, împreună cu formula lui Euler implică anumite identități trigonometrice, precum și formula lui de Moivre.

Formula lui Euler furnizează o legătură puternică între analiza matematică și trigonometrie, aducând o exprimare a funcțiilor sinus și cosinus ca sume ponderate ale funcției exponențiale:

${\displaystyle \cos x=\mathrm {Re} \{e^{ix}\}={e^{ix}+e^{-ix} \over 2}}$ 
${\displaystyle \sin x=\mathrm {Im} \{e^{ix}\}={e^{ix}-e^{-ix} \over 2i}}$ 

Cele două ecuații de mai sus pot fi deduse adunând și scăzând formulele lui Euler:

${\displaystyle e^{ix}=\cos x+i\sin x\;}$ 

${\displaystyle e^{-ix}=\cos(-x)+i\sin(-x)=\cos x-i\sin x\;}$ 

și rezolvând pentru cosinus sau sinus.

Aceste formule pot servi chiar ca definiții ale funcțiilor trigonometrice de argument complex x. De exemplu, dacă x = iy sunt valabile egalitățile:

${\displaystyle \cos(iy)={e^{-y}+e^{y} \over 2}=\cosh(y)}$ 

${\displaystyle \sin(iy)={e^{-y}-e^{y} \over 2i}=i\cdot \sinh(y).}$ 

Exponențialele complexe pot simplifica trigonometria, deoarece sunt mai ușor de utilizat decât componentele lor sinusoidale. Una din tehnici este de a converti pur și simplu sinusoidele în expresii echivalente în termeni de exponențiale. După prelucrări, rezultatul simplificat are valori reale. De exemplu:

${\displaystyle {\begin{aligned}\cos(x)\cdot \cos(y)&={\frac {(e^{ix}+e^{-ix})}{2}}\cdot {\frac {(e^{iy}+e^{-iy})}{2}}\\&={\frac {e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{4}}\\&={\frac {e^{i(x+y)}+e^{i(-x-y)}}{4}}+{\frac {e^{i(x-y)}+e^{i(-x+y)}}{4}}\\&={\frac {\cos(x+y)}{2}}+{\frac {\cos(x-y)}{2}}.\end{aligned}}}$ 

O altă tehnică este reprezentarea sinusoidelor în termeni de parte reală a unei expresii complexe, și de a face prelucrările pe acea expresie. De exemplu:

${\displaystyle {\begin{aligned}\cos(x\cdot n)+\cos(x\cdot (n-2))&=\mathrm {Re} \{\quad e^{ixn}+e^{ix(n-2)}\quad \}\\&=\mathrm {Re} \{\quad e^{ix(n-1)}\cdot (e^{ix}+e^{-ix})\quad \}\\&=\mathrm {Re} \{\quad e^{ix(n-1)}\cdot 2\cos(x)\quad \}\\&=\cos(x\cdot (n-1))\cdot 2\cos(x).\end{aligned}}}$ 

În ecuații diferențiale, funcția e^ix se folosește adesea pentru a simplifica derivările, chiar dacă rezultatul final este o funcție reală care implică sinus și cosinus. Identitatea lui Euler este o consecință imediată a formulei lui Euler.

În ingineria electrică dar și în alte domenii, semnalele ce pot varia periodic în timp sunt adesea descrise ca o combinație ponderată de sinus și cosinus, și acestea se exprimă mai convenabil ca partea reală a funcțiilor exponențiale cu exponent imaginar, folosind formula lui Euler. De asemenea, analiza fazorială a circuitelor poate include formula lui Euler pentru reprezentarea impedanței unui capacitor sau a unui inductor.

Folosind seriile Taylor

Aceasta este o demonstrație a formulei lui Euler folosind dezvoltări în serie Taylor și proprietățile puterilor lui i:

${\displaystyle {\begin{aligned}i^{0}&{}=1,\quad &i^{1}&{}=i,\quad &i^{2}&{}=-1,\quad &i^{3}&{}=-i,\\i^{4}&={}1,\quad &i^{5}&={}i,\quad &i^{6}&{}=-1,\quad &i^{7}&{}=-i,\\\end{aligned}}}$ 

și așa mai departe. Funcțiile e^x, cos(x) și sin(x) (presupunând că x este număr real) pot fi exprimate folosind dezvoltările lor în serie Taylor în jurul lui zero:

${\displaystyle {\begin{aligned}e^{x}&{}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots \\\cos x&{}=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\\sin x&{}=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \end{aligned}}}$ 

Pentru z complex se definește fiecare funcție prin seriile de mai sus, înlocuind x cu z. Aceasta este posibil, deoarece raza de convergență a fiecărei serii este infinită. Atunci rezultă că

${\displaystyle {\begin{aligned}e^{iz}&{}=1+iz+{\frac {(iz)^{2}}{2!}}+{\frac {(iz)^{3}}{3!}}+{\frac {(iz)^{4}}{4!}}+{\frac {(iz)^{5}}{5!}}+{\frac {(iz)^{6}}{6!}}+{\frac {(iz)^{7}}{7!}}+{\frac {(iz)^{8}}{8!}}+\cdots \\&{}=1+iz-{\frac {z^{2}}{2!}}-{\frac {iz^{3}}{3!}}+{\frac {z^{4}}{4!}}+{\frac {iz^{5}}{5!}}-{\frac {z^{6}}{6!}}-{\frac {iz^{7}}{7!}}+{\frac {z^{8}}{8!}}+\cdots \\&{}=\left(1-{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}-{\frac {z^{6}}{6!}}+{\frac {z^{8}}{8!}}-\cdots \right)+i\left(z-{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}-{\frac {z^{7}}{7!}}+\cdots \right)\\&{}=\cos(z)+i\sin(z)\end{aligned}}}$ 

Rearanjarea termenilor se justifică deoarece fiecare serie este absolut convergentă. Luând z = x număr real rezultă identitatea originală așa cum a descoperit-o Euler.

Folosind derivata

Pornind de la o reprezentare geometrică a funcțiilor trigonometrice se poate ajunge la formula exponențială complexă.

Se definește o funcție ${\displaystyle f}$  prin următoarea expresie algebrică:

${\displaystyle f(x)={\frac {\cos x+i\sin x}{e^{ix}}}={\frac {f_{1}(x)+f_{2}(x)}{g(x)}}.\ }$ 

unde cosinusul și sinusul sunt notate f₁(x) și f₂(x), urmând a exprima și derivatele acestor funcții prin aceleași notații datorită valorilor acestor derivate.

Aceasta este permisă deoarece ecuația

${\displaystyle e^{ix}\cdot e^{-ix}=e^{0}=1\ }$ 

implică faptul că ${\displaystyle e^{ix}}$  nu este niciodată zero.

Derivata funcției ${\displaystyle f}$ , conform regulii câtului și tratând unitatea imaginară i ca pe o constantă oarecare, este nulă:

${\displaystyle {\begin{aligned}f'(x)&{}={\frac {(-\sin x+i\cos x)\cdot e^{ix}-(\cos x+i\sin x)\cdot i\cdot e^{ix}}{(e^{ix})^{2}}}\\&{}={\frac {-\sin x\cdot e^{ix}-i^{2}\sin x\cdot e^{ix}}{(e^{ix})^{2}}}\\&{}={\frac {-\sin x\cdot e^{ix}+\sin x\cdot e^{ix}}{(e^{ix})^{2}}}\\&{}=0.\end{aligned}}}$ 

Deci, ${\displaystyle f\ }$  având derivata nulă trebuie să fie o funcție constantă. Astfel,

${\displaystyle {\frac {\cos x+i\sin x}{e^{ix}}}=f(x)=f(0)={\frac {\cos 0+i\sin 0}{e^{0}}}=1.}$ 

Rearanjând, rezultă că

${\displaystyle \displaystyle \cos x+i\sin x=e^{ix}.}$ 

Folosind egalități între derivate și funcții

Tot de la reprezentarea geometrică a funcțiilor trigonometrice se poate ajunge la formula exponențială complexă.

Se consideră funcția g(x) prin

${\displaystyle g(x)\ {\stackrel {\mathrm {def} }{=}}\ e^{ix}.\ }$ 

i fiind constantă, primele două derivate ale lui g(x) sunt

${\displaystyle g'(x)=ie^{ix}\ }$ 
${\displaystyle g''(x)=i^{2}e^{ix}=-e^{ix}\ }$ 

deoarece i ² = −1 prin definiție. De aici se poate scrie următoarea egalitate între derivata de ordinul doi și funcția inițială cu semn schimbat, adică o ecuație diferențială ordinară liniară de ordinul 2:

${\displaystyle g''(x)=-g(x)\ }$ 

sau

${\displaystyle g''(x)+g(x)=0.\ }$ 

Pentru această egalitate se constată existența a două funcții reale pentru care este valabilă egalitatea: atât cos(x) cât și sin(x) sunt funcții reale a căror a doua derivată este identică cu funcția inițială cu semnul minus.

${\displaystyle g_{1}(x)=\cos(x)\ }$ 
${\displaystyle g_{2}(x)=\sin(x).\ }$ 

Aceste două funcții sunt soluțiile acestei ecuații diferențiale liniare de ordinul doi. Ecuația admite și orice sumă a acestor două funcții înmulțite cu constante numerice oarecare (combinație liniară de soluții particulare ale unei ecuații diferențiale omogene) tot ca o soluție. Atunci, în general, soluția ecuației diferențiale este

${\displaystyle g(x)\,}$	${\displaystyle =Ag_{1}(x)+Bg_{2}(x)\ }$
	${\displaystyle =A\cos(x)+B\sin(x)\ }$

pentru orice constante A și B. Dar nu toate valorile acestor două constante satisfac condițiile particularizatoare pentru funcția g(x) specificată mai sus:

${\displaystyle g(0)=e^{i0}=1\ }$ 
${\displaystyle g'(0)=ie^{i0}=i\ }$ .

Condițiile inițiale (aplicate soluției generale) sunt

${\displaystyle g(0)=A\cos(0)+B\sin(0)=A\ }$ 
${\displaystyle g'(0)=-A\sin(0)+B\cos(0)=B\ }$ 

și permit obținerea valorilor pentru A și B

${\displaystyle g(0)=A=1\ }$ 
${\displaystyle g'(0)=B=i\ }$ 

și în final egalitatea de demonstrat:

${\displaystyle g(x)\ {\stackrel {\mathrm {def} }{=}}\ e^{ix}=\cos(x)+i\sin(x).\ }$