Satz Von Ptolemäus: Mathematischer Satz
Der Satz des Ptolemäus (nach Claudius Ptolemäus) ist ein Lehrsatz der Elementargeometrie, der eine Beziehung zwischen den Seiten und Diagonalen eines Sehnenvierecks beschreibt.
Er lässt sich auffassen als Verallgemeinerung des pythagoreischen Lehrsatzes und ergibt sich selbst auch als Grenzfall des Satzes von Casey.
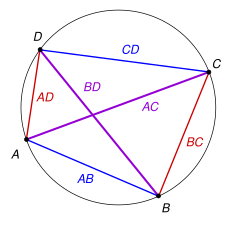

Aussage
Der Satz des Ptolemäus lautet:
- In einem Sehnenviereck ist das Produkt der Längen der Diagonalen gleich der Summe der Produkte der Längen gegenüberliegender Seiten.
In einem Sehnenviereck 
Zudem gilt auch die Umkehrung des Satzes von Ptolemäus, das heißt stimmt in einem konvexen Viereck das Produkt der Diagonalen mit der Summe der Produkte der gegenüberliegenden Seiten überein, so handelt es sich um ein Sehnenviereck. Für Vierecke, die keine Sehnenvierecke sind, gilt die folgende Aussage, die auch als Ungleichung des Ptolemäus bezeichnet wird:
- Sei
ein Dreieck und D ein Punkt, der nicht auf dem Bogen
des Umkreises liegt, so gilt:
Elementargeometrischer Beweis

Bei einem Sehnenviereck 




Da D nun aber auf dem Umkreis von 

Mit den obigen Gleichungen liefert dies:
Liegt D nicht auf dem Umkreis, so gilt aufgrund der Dreiecksungleichung für 
Die obigen Gleichungen liefern damit dann die Ungleichung des Ptolemäus:
Beweis des Ptolemäischen Lehrsatzes im Komplexen
Neben der Möglichkeit, den Beweis elementargeometrisch zu führen, lässt sich der Ptolemäische Lehrsatz auch leicht mit Methoden der komplexen Analysis beweisen, indem man die Eigenschaften der komplexen Umkehrfunktion:
ausnutzt.
Die komplexe Umkehrfunktion zählt zu den Möbiustransformationen, welche in der komplexen Analysis als stetige Transformationen der erweiterten komplexen Zahlenebene behandelt werden.
(I) Vereinfachung des Problems
Zunächst darf man oBdA annehmen, dass die Figur, welche aus dem gegebenen Sehnenviereck 


Dabei darf man weiter annehmen, dass eine spezielle Figur mit 


(II) Ausnutzung der geometrischen Eigenschaften der Umkehrfunktion
Wesentlich für den Beweis ist nun die Tatsache, dass für die Kreislinie 





Da nun auf dem punktierten Kreisbogen der Punkt 





(III) Eigentliche Berechnung
Aus (II) ergibt sich unter Benutzung der komplexen Betragsfunktion 
und damit:
und dann nach Erweitern mit 
und weiter wegen 
Dies aber ist nichts weiter als die oben behauptete und zu beweisende Identität.
Folgerungen
Satz des Pythagoras
Jedes Rechteck ist ein Sehnenviereck, in welchem – mit den obigen Bezeichnungen – die Gleichungen 
Sehnen des Umkreises eines gleichseitigen Dreiecks

Gegeben seien ein gleichseitiges Dreieck 







Beweis:
In der abgebildeten Figur ist ohne Beschränkung der Allgemeinheit 



und somit
.
Verallgemeinerungen (Metrische Räume und Riemannsche Mannigfaltigkeiten)
In CAT(0)-Räumen 
für alle
.
Für vollständige Riemannsche Mannigfaltigkeiten gilt auch die Umkehrung: wenn die Ptolemäische Ungleichung für alle Punkte gilt, dann handelt es sich um einen CAT(0)-Raum.
Wenn eine Riemannsche Mannigfaltigkeit nichtpositive Schnittkrümmung hat, dann ist sie lokal ptolemäisch, d. h. zu jedem Punkt gibt es eine Umgebung, innerhalb derer die Ptolemäische Ungleichung gilt.
Literatur
- Erwin Just, Norman Schaumberger: Vector Approach to Ptolemy’s Theorem. Mathematics Magazine, Vol. 77, No. 5, 2004, S. 386–88 (JSTOR:3219205)
- John Roe: Elementary Geometry (= Oxford science publications). Oxford University Press, Oxford [u. a.] 1993, ISBN 0-19-853457-4.
- Anna Maria Fraedrich: Die Satzgruppe des Pythagoras (= Lehrbücher und Monographien zur Didaktik der Mathematik. Band 29). B.I.-Wissenschaftsverlag, Mannheim / Leipzig / Wien / Zürich 1994, ISBN 3-411-17321-1.
- Klaus Gürlebeck, Klaus Habetha, Wolfgang Sprößig: Funktionentheorie in der Ebene und im Raum. Birkhäuser Verlag, Basel [u. a.] 2006, ISBN 978-3-7643-7369-6.
- Helmut Karzel, Hans-Joachim Kroll: Geschichte der Geometrie seit Hilbert. Wissenschaftliche Buchgesellschaft, Darmstadt 1988, ISBN 3-534-08524-8.
- Hugo Fenkner, Karl Holzmüller: Mathematisches Unterrichtswerk. Nach den Richtlinien für die Lehrpläne der höheren Schulen Preußens neu bearbeitet von Dr. Karl Holzmüller. Geometrie. Ausgabe A in 2 Teilen. I. Teil. 12. Auflage. Verlag von Otto Salle, Berlin 1926.
- Theophil Lambacher, Wilhelm Schweizer (Hrsg.): Lambacher-Schweizer. Mathematisches Unterrichtswerk für höhere Schulen. Geometrie. Ausgabe E. Teil 2. 13. Auflage. Ernst Klett Verlag, Stuttgart 1965.
Einzelnachweise
This article uses material from the Wikipedia Deutsch article Satz von Ptolemäus, which is released under the Creative Commons Attribution-ShareAlike 3.0 license ("CC BY-SA 3.0"); additional terms may apply (view authors). Abrufstatistik · Autoren Der Inhalt ist verfügbar unter CC BY-SA 4.0, sofern nicht anders angegeben. Images, videos and audio are available under their respective licenses.
®Wikipedia is a registered trademark of the Wiki Foundation, Inc. Wiki Deutsch (DUHOCTRUNGQUOC.VN) is an independent company and has no affiliation with Wiki Foundation.













