Бутылка Клейна

Тесно связана с лентой Мёбиуса и проективной плоскостью. Название, по-видимому, происходит от схожести написания слов нем. Fläche (поверхность) и нем. Flasche (бутылка).

Первое описание бутылки Клейна появилось в монографии Ф. Клейна «О теории Римана алгебраических функций и их интегралов», вышедшей в 1882 году. В ней Клейн так описывает эту поверхность:

О ней можно составить себе представление, если вывернуть кусок каучуковой трубки и заставить его пересечься с самим собой таким образом, чтобы при соединении его концов его внешняя сторона соединилась бы с внутренней.

Оригинальный текст (нем.)

Man kann sich von denselben ein Bild machen, indem man etwa ein Stück eines Kautschukschlauches umstülpt und nun so sich selbst durchdringen lässt, dass bei Zusammenbiegung der Enden die Aussenseite mit der Innenseite zusammenkommt.

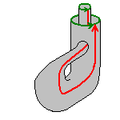
Чтобы построить модель бутылки Клейна, понадобится бутылка с двумя дополнительными отверстиями: в донышке и в стенке. Горлышко бутылки нужно вытянуть, изогнуть вниз и, продев его через отверстие в стенке, присоединить к отверстию на дне бутылки. Для настоящей бутылки Клейна в четырёхмерном пространстве отверстие в стенке не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве.

В отличие от обыкновенного стакана, у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара, можно пройти путь изнутри наружу, не пересекая поверхность (то есть на самом деле у этого объекта нет «внутри» и нет «снаружи»).

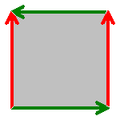
Более формально, бутылку Клейна можно получить склеиванием квадрата ${\displaystyle [0,1]\times [0,1]}$ , отождествляя точки ${\displaystyle (0,y)\sim (1,y)}$  при ${\displaystyle 0\leqslant y\leqslant 1}$  и ${\displaystyle (x,0)\sim (1-x,1)}$  при ${\displaystyle 0\leqslant x\leqslant 1}$ , как показано на первой диаграмме. Следующие диаграммы показывают как эта топология погружается в бутылочную форму 3D.

• Подобно ленте Мёбиуса, бутылка Клейна является двумерным дифференцируемым неориентируемым многообразием. В отличие от ленты Мёбиуса, бутылка Клейна является замкнутым многообразием, то есть компактным многообразием без края.
• Бутылка Клейна не может быть вложена (только погружена) в трёхмерное евклидово пространство ${\displaystyle \mathbb {R} ^{3}}$ , но вкладывается в ${\displaystyle \mathbb {R} ^{4}}$ .
• Бутылка Клейна может быть получена склеиванием двух лент Мёбиуса по краю. Однако в обычном трёхмерном евклидовом пространстве ${\displaystyle \mathbb {R} ^{3}}$  сделать это, не создав самопересечения, невозможно.
• Хроматическое число поверхности равно 6.

 

 

Если разрезать бутылку Клейна пополам по её плоскости симметрии, то результатом будет лента Мёбиуса, изображённая справа. (При этом необходимо помнить, что изображённого самопересечения на самом деле нет.)

Бутылка Клейна в виде восьмёрки имеет довольно простую параметризацию:

${\displaystyle x=\left(r+\cos {\tfrac {u}{2}}\cdot \sin v-\sin {\tfrac {u}{2}}\cdot \sin 2v\right)\cdot \cos u}$ 
${\displaystyle y=\left(r+\cos {\tfrac {u}{2}}\cdot \sin v-\sin {\tfrac {u}{2}}\cdot \sin 2v\right)\cdot \sin u}$ 
${\displaystyle z=\sin {\tfrac {u}{2}}\cdot \sin v+\cos {\tfrac {u}{2}}\cdot \sin 2v}$ 

В этом виде самопересечение имеет форму геометрического круга в плоскости ${\displaystyle XY}$ . Константа ${\displaystyle r}$  равна радиусу круга. Параметр ${\displaystyle u}$  задаёт угол на плоскости ${\displaystyle XY}$  и ${\displaystyle v}$  обозначает положение около 8-образного сечения.

• Топология
• Алгебраическая топология
• Поверхность
• Лента Мёбиуса