Hilberts Axiomensystem Der Euklidischen Geometrie: Begriff der Geometrie

Über die Natur dieser „Dinge“ und auch ihrer „Beziehungen“ macht Hilbert als Formalist keinerlei Annahmen. Sie sind ausschließlich implizit definiert, nämlich durch ihre Verknüpfung in einem Axiomensystem.

Hilbert soll einmal gesagt haben, man könne statt „Punkte, Geraden und Ebenen“ jederzeit auch „Tische, Stühle und Bierseidel“ sagen; es komme nur darauf an, dass die Axiome erfüllt sind. Allerdings hat er große Mühe darauf verwandt, dass seine „Tische, Stühle und Bierseidel“ all die Gesetzmäßigkeiten erfüllen, die die Geometer der vorhergegangenen zweitausend Jahre für „Punkte, Geraden und Ebenen“ herausgefunden haben. Die Stärke der axiomatischen Vorgehensweise liegt nicht darin, dass sie von der Wirklichkeit absieht. Sie erlaubt es aber, durch Abänderung der Axiome und Analyse ihres Zusammenhangs die logische Struktur, der diese Wirklichkeit folgt, in einer vorher nicht denkbaren Weise zu durchleuchten.

Auf ein gegenüber dem Hilbertschen System abgeschwächtes Axiomensystem ohne Parallelenaxiom lässt sich die absolute Geometrie begründen: Dort gibt es dann entweder keine Parallelen (elliptische Geometrie) oder durch einen Punkt außerhalb einer Geraden beliebig viele Parallelen (hyperbolische Geometrie). Die hyperbolische Geometrie erfüllt Hilberts Axiomengruppen I–III und V, die elliptische Geometrie I, II und V und eine schwächere Version der Kongruenzaxiome (III).

Zu diesem Zweck verknüpft Hilbert die „Dinge“ und „Beziehungen“ durch 21 Axiome in fünf Gruppen:

Axiome der Verknüpfung (oder Inzidenz; Gruppe I)

Mit diesen Axiomen soll der Begriff liegen implizit definiert werden. Hilbert verwendet hier den Begriff bestimmen oder zusammengehören und eine Reihe anderer Sprechweisen: ${\displaystyle g}$  geht durch ${\displaystyle P}$ , ${\displaystyle g}$  verbindet ${\displaystyle P}$  und ${\displaystyle Q}$ , ${\displaystyle P}$  liegt auf ${\displaystyle g}$ , ${\displaystyle P}$  ist ein Punkt von ${\displaystyle g}$ , auf ${\displaystyle g}$  gibt es den Punkt ${\displaystyle P}$  usw. Heute spricht man in der Mathematik von Inzidenz: „${\displaystyle P}$  inzidiert ${\displaystyle g}$ “ (formal: ${\displaystyle PIg}$ ).

• I.1. Zwei voneinander verschiedene Punkte ${\displaystyle P}$  und ${\displaystyle Q}$  bestimmen stets eine Gerade ${\displaystyle g}$ .
• I.2. Irgend zwei voneinander verschiedene Punkte einer Geraden bestimmen diese Gerade.
• I.3. Auf einer Geraden gibt es stets wenigstens zwei Punkte, in einer Ebene gibt es stets wenigstens drei nicht auf einer Geraden gelegene Punkte.
• I.4. Drei nicht auf ein und derselben Geraden liegende Punkte ${\displaystyle P,Q,R}$  bestimmen stets eine Ebene.
• I.5. Irgend drei Punkte einer Ebene, die nicht auf ein und derselben Geraden liegen, bestimmen diese Ebene.
• I.6. Wenn zwei Punkte ${\displaystyle P}$  und ${\displaystyle Q}$  einer Geraden ${\displaystyle g}$  in einer Ebene ${\displaystyle \alpha }$  liegen, so liegt jeder Punkt von ${\displaystyle g}$  in ${\displaystyle \alpha }$ .
• I.7. Wenn zwei Ebenen ${\displaystyle \alpha }$  und ${\displaystyle \beta }$  einen Punkt ${\displaystyle P}$  gemeinsam haben, so haben sie wenigstens noch einen weiteren Punkt ${\displaystyle Q}$  gemeinsam.
• I.8. Es gibt wenigstens vier nicht in einer Ebene gelegene Punkte.

•  
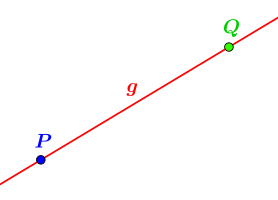
  Veranschaulichung Axiome I.1. und I.2.
•  
  Veranschaulichung Axiome I.3., I.4., I.5. und I.6.
•  
  Veranschaulichung Axiome I.7., und I.8.

Die Axiome 1–3 heißen ebene Axiome der Gruppe I und Axiome 4–8 räumliche Axiome der Gruppe I.

Aus diesen Axiomen allein lässt sich zum Beispiel folgern,

• dass zwei verschiedene Geraden sich in genau einem Punkt oder überhaupt nicht schneiden,
• dass zwei verschiedene Ebenen sich in genau einer Geraden oder überhaupt nicht schneiden,
• dass eine Ebene und eine nicht in ihr liegende Gerade sich in genau einem Punkt oder überhaupt nicht schneiden,
• dass eine Gerade und ein nicht auf ihr liegender Punkt eine Ebene bestimmen,
• dass zwei verschiedene, sich schneidende Geraden eine Ebene bestimmen.

Axiome der Anordnung (Gruppe II)

Mit diesen wird der Begriff zwischen definiert als eine Beziehung zwischen drei Punkten. Wird von drei Punkten gesagt, dass der eine zwischen den beiden anderen liegt, so ist damit stets ausgedrückt, dass es verschiedene Punkte sind, und dass sie auf einer Geraden liegen. Unter dieser Voraussetzung lassen sich die folgenden Axiome sehr kurz formulieren:

• II.1. Wenn ${\displaystyle B}$  zwischen ${\displaystyle A}$  und ${\displaystyle C}$  liegt, so liegt ${\displaystyle B}$  auch zwischen ${\displaystyle C}$  und ${\displaystyle A}$ .
• II.2. Zu zwei Punkten ${\displaystyle A}$  und ${\displaystyle C}$  gibt es stets wenigstens einen Punkt ${\displaystyle B}$ , der zwischen ${\displaystyle A}$  und ${\displaystyle C}$  liegt, und wenigstens einen Punkt ${\displaystyle D}$ , so dass ${\displaystyle C}$  zwischen ${\displaystyle A}$  und ${\displaystyle D}$  liegt.
• II.3. Unter irgend drei Punkten einer Geraden gibt es stets einen und nur einen Punkt, der zwischen den beiden anderen liegt.

Auf Grund dieser Axiome lässt sich definieren, was eine Strecke ${\displaystyle AB}$  ist: Die Menge aller Punkte, die zwischen ${\displaystyle A}$  und ${\displaystyle B}$  liegen. (Die Strecken ${\displaystyle AB}$  und ${\displaystyle BA}$  sind nach dieser Definition identisch.) Der Begriff Strecke wird benötigt, um das folgende Axiom zu formulieren:

• II.4. Es seien ${\displaystyle A,B,C}$  drei nicht in gerader Linie gelegene Punkte und ${\displaystyle a}$  eine Gerade in der Ebene ${\displaystyle ABC}$ , die keinen dieser drei Punkte trifft; wenn dann die Gerade ${\displaystyle a}$  durch einen Punkt der Strecke ${\displaystyle AB}$  geht, so geht sie gewiss auch entweder durch einen Punkt der Strecke ${\displaystyle BC}$  oder durch einen Punkt der Strecke ${\displaystyle AC}$ .

Dieses Axiom heißt auch das Axiom von Pasch; es hat eine besondere wissenschaftsgeschichtliche Bedeutung, da es bei Euklid nicht vorkommt.

•  
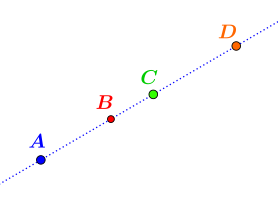
  Veranschaulichung Axiome II.1., II.2. und II.3.
•  
  Veranschaulichung Axiom II.4.

Aus den Axiomen der Verknüpfung (Inzidenz) und der Anordnung folgt bereits, dass zwischen zwei gegebenen Punkten einer Geraden stets noch unendlich viele weitere Punkte liegen, dass die Punkte einer Geraden also in sich dicht liegen. Ferner lässt sich zeigen, dass jede Gerade als Punktmenge auf genau zwei Weisen geordnet werden kann, so dass ein Punkt ${\displaystyle C}$  genau dann zwischen den Punkten ${\displaystyle A}$  und ${\displaystyle B}$  liegt, wenn ${\displaystyle A$  oder ${\displaystyle B$  ist.

Weiter lässt sich folgern, dass jede Gerade (und jeder in einer Ebene gelegene und sich nicht selbst schneidende Streckenzug) eine Ebene in zwei Gebiete aufteilt. Genauso trennt jede Ebene den Raum in zwei Gebiete.

Siehe auch: Ordnung und Seiteneinteilung

Axiome der Kongruenz (Gruppe III)

Die dritte Axiomgruppe definiert den Begriff kongruent als eine Beziehung zwischen Strecken und zwischen Winkeln. Eine andere Bezeichnung hierfür ist gleich oder (bei Strecken) gleich lang. Als Zeichen hierfür verwendet Hilbert ${\displaystyle \equiv }$ .

• III.1. Wenn ${\displaystyle A}$  und ${\displaystyle B}$  zwei Punkte auf einer Geraden ${\displaystyle a}$  sind und ferner ${\displaystyle A^{\prime }}$  ein Punkt auf derselben oder einer anderen Geraden ${\displaystyle a^{\prime }}$  ist, so kann man auf einer gegebenen Seite der Geraden ${\displaystyle a^{\prime }}$  von ${\displaystyle A^{\prime }}$  stets einen Punkt ${\displaystyle B^{\prime }}$  finden, so dass die Strecke ${\displaystyle AB}$  der Strecke ${\displaystyle A^{\prime }B^{\prime }}$  kongruent (oder gleich) ist, in Zeichen: ${\displaystyle AB\equiv A^{\prime }B^{\prime }}$ .

Von jedem Punkt aus kann also jede beliebige Strecke abgetragen werden. Dass diese Abtragung eindeutig ist, lässt sich aus der Gesamtheit der Axiome I–III beweisen, ebenso, dass AB ≡ AB ist und dass aus ${\displaystyle AB\equiv A^{\prime }B^{\prime }}$  stets ${\displaystyle A^{\prime }B^{\prime }\equiv AB}$  folgt (Reflexivität und Symmetrie).

• III.2. Wenn eine Strecke zu zwei anderen Strecken kongruent ist, so sind diese auch zueinander kongruent; formaler: wenn ${\displaystyle AB\equiv A^{\prime }B^{\prime }}$  und ${\displaystyle AB\equiv A^{\prime \prime }B^{\prime \prime }}$ , so ist ${\displaystyle A^{\prime }B^{\prime }\equiv A^{\prime \prime }B^{\prime \prime }}$ .

Es wird also gefordert, dass die Kongruenz-Relation transitiv ist. Damit ist sie eine Äquivalenzrelation.

• III.3. Es seien ${\displaystyle AB}$  und ${\displaystyle BC}$  zwei Strecken ohne gemeinsame Punkte auf der Geraden ${\displaystyle a}$  und ferner ${\displaystyle A^{\prime }B^{\prime }}$  und ${\displaystyle B^{\prime }C^{\prime }}$  zwei Strecken auf derselben oder einer anderen Geraden ${\displaystyle a^{\prime }}$  ebenfalls ohne gemeinsame Punkte; wenn dann ${\displaystyle AB\equiv A^{\prime }B^{\prime }}$  und ${\displaystyle BC\equiv B^{\prime }C^{\prime }}$ , so ist auch stets ${\displaystyle AC\equiv A^{\prime }C^{\prime }}$ .

Beim Zusammenfügen (Addieren) von Strecken bleibt die Kongruenz also erhalten.

Ein Winkel wird nun definiert als ein ungeordnetes (!) Paar von Halbgeraden, die von einem gemeinsamen Punkt ${\displaystyle S}$  ausgehen und nicht zur selben Geraden gehören. (Zwischen ${\displaystyle \sphericalangle (h,g)}$  und ${\displaystyle \sphericalangle (g,h)}$  wird also nicht unterschieden; auch gibt es nach dieser Definition weder überstumpfe noch gestreckte Winkel.) Es kann auch definiert werden, was das Innere eines Winkels ${\displaystyle \sphericalangle (g,h)}$  ist: Es sind dies all diejenigen Punkte der von ${\displaystyle g}$  und ${\displaystyle h}$  aufgespannten Ebene, die mit ${\displaystyle h}$  zusammen auf der gleichen Seite von ${\displaystyle g}$  und mit ${\displaystyle g}$  zusammen auf der gleichen Seite von ${\displaystyle h}$  liegen. Ein Winkel umfasst stets weniger als eine Halbebene.

• III.4. Es sei ein Winkel ${\displaystyle \sphericalangle (h,g)}$  in einer Ebene ${\displaystyle \alpha }$  und eine Gerade ${\displaystyle a^{\prime }}$  in einer Ebene ${\displaystyle \alpha ^{\prime }}$ , sowie eine bestimmte Seite von ${\displaystyle a^{\prime }}$  auf ${\displaystyle \alpha ^{\prime }}$  gegeben. Es bedeute ${\displaystyle h^{\prime }}$  einen Halbstrahl der Geraden ${\displaystyle a^{\prime }}$ ; dann gibt es in der Ebene ${\displaystyle \alpha ^{\prime }}$  einen und nur einen Halbstrahl ${\displaystyle g^{\prime }}$ , so dass der Winkel ${\displaystyle \sphericalangle (h,g)}$  kongruent (oder gleich) dem Winkel ${\displaystyle \sphericalangle (h',g')}$  ist und zugleich alle inneren Punkte des Winkels ${\displaystyle \sphericalangle (h',g')}$  auf der gegebenen Seite von ${\displaystyle a^{\prime }}$  liegen.
  In Zeichen: ${\displaystyle \sphericalangle (h,g)\equiv \sphericalangle (h',g')}$ .
  Jeder Winkel ist sich selbst kongruent, das heißt, es ist stets ${\displaystyle \sphericalangle (h,g)\equiv \sphericalangle (h,g)}$ .

Kurz gesagt bedeutet dies: Ein jeder Winkel kann in einer gegebenen Ebene an einen gegebenen Halbstrahl nach einer gegebenen Seite dieses Halbstrahls auf eine eindeutig bestimmte Weise abgetragen werden.

Es fällt auf, dass die Eindeutigkeit der Konstruktion und die Selbstkongruenz hier (im Gegensatz zu der Kongruenz von Strecken) axiomatisch festgelegt werden muss.

• III.5. Aus ${\displaystyle \sphericalangle (h,g)\equiv \sphericalangle (h',g')}$  und ${\displaystyle \sphericalangle (h,g)\equiv \sphericalangle (h'',g'')}$  folgt ${\displaystyle \sphericalangle (h',g')\equiv \sphericalangle (h'',g'')}$ .

Aus diesem Axiom folgt mit der Selbstkongruenz, dass die Kongruenz für Winkel eine transitive und symmetrische Relation ist.

Nachdem in naheliegender Weise definiert wurde, was unter ${\displaystyle \sphericalangle ABC}$  zu verstehen ist, lässt sich auch das letzte Kongruenzaxiom formulieren:

• III.6. Wenn für zwei Dreiecke ${\displaystyle ABC}$  und ${\displaystyle A^{\prime }B^{\prime }C^{\prime }}$  die Kongruenzen
  ${\displaystyle AB\equiv A'B',\quad AC\equiv A'C'\quad {\text{und}}\quad \sphericalangle BAC\equiv \sphericalangle B'A'C'}$ 

gelten, so sind auch stets die Kongruenzen
${\displaystyle \sphericalangle ABC\equiv \sphericalangle A'B'C'\quad {\text{und}}\quad \sphericalangle ACB\equiv \sphericalangle A'C'B'}$ 
erfüllt.

•  
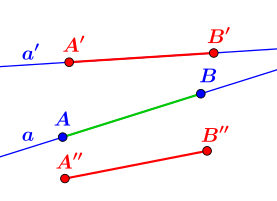
  Veranschaulichung Axiome III.1. und III.2.
•  
  Veranschaulichung Axiome III.3.
•  
  Veranschaulichung Axiom III.4.
•  
  Veranschaulichung Axiome III.5. und III.6.

Es handelt sich hier um den Kongruenzsatz „sws“, den Hilbert als Axiom setzt. Euklid formuliert hierfür einen „Beweis“ (I L. 1), gegen den Peletarius 1557 erstmals Bedenken formuliert hat. Hilbert hat gezeigt, dass dieser Satz, oder jedenfalls sein wesentlicher Inhalt, als Axiom unentbehrlich ist.

Die übrigen Kongruenzsätze lassen sich hieraus beweisen, ebenso die Addierbarkeit von Winkeln. Es lässt sich eine ${\displaystyle <}$ -Beziehung unter Winkeln definieren, die mit der Kongruenz verträglich ist.

Weiter definiert Hilbert den Begriff Nebenwinkel in naheliegender Weise, und den Begriff rechter Winkel als einen Winkel, der mit seinem Nebenwinkel kongruent ist.

Es lässt sich dann zeigen, dass alle rechten Winkel zueinander kongruent sind. Euklid hatte dies – wohl unnötigerweise – als Axiom gesetzt.

Siehe auch: Kongruenz und präeuklidische Ebene

Axiom der Parallelen (Gruppe IV)

• IV. (auch Euklidisches Axiom.) Es sei ${\displaystyle g}$  eine beliebige Gerade und ${\displaystyle P}$  ein Punkt außerhalb von ${\displaystyle g}$ . Dann gibt es in der durch ${\displaystyle g}$  und ${\displaystyle P}$  bestimmten Ebene höchstens eine Gerade ${\displaystyle g^{\prime }}$ , die durch ${\displaystyle P}$  verläuft und ${\displaystyle g}$  nicht schneidet.

Dass es mindestens eine solche Gerade gibt, folgt aus den Axiomen I–III und unmittelbar aus dem daraus hergeleiteten Satz vom Außenwinkel. Diese einzige Gerade ${\displaystyle g^{\prime }}$  heißt die Parallele zu ${\displaystyle g}$  durch ${\displaystyle P}$ .

Dieses Axiom mit seinen Voraussetzungen und Folgerungen ist wahrscheinlich der meistdiskutierte Gegenstand der Geometrie. Siehe dazu auch: Parallelenproblem

Als ein zum Parallelenaxiom äquivalentes Axiom gibt Hilbert an:

Schneiden zwei Geraden ${\displaystyle a,b}$  eine dritte Gerade ${\displaystyle c}$  nicht, obwohl diese mit ihnen in der gleichen Ebene liegt, so schneiden sie sich auch untereinander nicht.

Ferner folgt aus den Axiomen I–IV, dass die Winkelsumme im Dreieck zwei Rechte beträgt. Ein Äquivalent zum Parallelenaxiom wird dieser Winkelsummensatz erst, wenn man das Archimedische Axiom (V.1) hinzuzieht.

Unter diesen Voraussetzungen lässt sich das Axiom auch gleichwertig so formulieren (vergleiche dazu Saccheri-Viereck):

Es existiert ein Rechteck.

•  
  Veranschaulichung Axiom IV.

Axiome der Stetigkeit (Gruppe V)

• V.1. (Axiom des Messens oder Archimedisches Axiom). Sind ${\displaystyle AB}$  und ${\displaystyle CD}$  irgendwelche Strecken, so gibt es eine Anzahl ${\displaystyle n}$  derart, dass das ${\displaystyle n}$ -malige Hintereinanderabtragen der Strecke ${\displaystyle CD}$  von ${\displaystyle A}$  aus auf den durch ${\displaystyle B}$  gehenden Halbstrahl über den Punkt ${\displaystyle B}$  hinausführt.

Durch jede noch so kleine Strecke ${\displaystyle CD}$  lässt sich also, wenn man sie nur oft genug aneinandersetzt, jede noch so große Strecke ${\displaystyle AB}$  übertreffen. Man könnte auch sagen: Es gibt keine „unendlich kleinen“ oder „unendlich großen“ Strecken; die natürlichen Zahlen reichen aus, um alle Strecken vergleichbar (im Sinne von größer, kleiner, gleich) zu machen.

•  
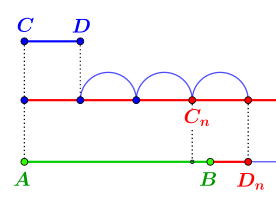
  Veranschaulichung Axiom V.1.

• V.2. (Axiom der (linearen) Vollständigkeit) Zu den Punkten einer Geraden können, bei Erhalt ihrer Anordnungs- und Kongruenzbeziehungen, keine weiteren Punkte hinzugefügt werden, ohne dass die unter den vorherigen Elementen bestehenden Beziehungen, die aus den Axiomen I–III folgenden Grundeigenschaften der linearen Anordnung und Kongruenz oder aber das Axiom V.1 verletzt wird.

Die euklidische Geometrie ist also die größtmögliche Geometrie, die den vorhergehenden Axiomen entspricht. Sie ist damit vollständig im gleichen Sinne, wie reelle Zahlen vollständig sind. Deshalb lässt sich auch die analytische Geometrie des ${\displaystyle \mathbb {R} ^{3}}$  als Modell für die euklidische Geometrie verwenden.

Deutlicher wird dies noch in dem – aus V.2 folgenden – „Vollständigkeitssatz“:

• Die Elemente (Punkte, Geraden und Ebenen) der Geometrie bilden ein System, das bei Aufrechterhaltung sämtlicher Axiome zu keiner Erweiterung durch zusätzliche Punkte, Geraden und/oder Ebenen mehr fähig ist.

Ohne das Archimedische Axiom ist diese Forderung nicht erfüllbar. Vielmehr lässt sich jede Geometrie, die den Axiomen I–IV, aber nicht V.1, entspricht, noch durch zusätzliche Elemente erweitern. Es entstehen dann Nichtstandard-Systeme.

Andererseits ist auch das Vollständigkeitsaxiom V.2 unentbehrlich, es lässt sich nicht aus den Axiomen I–V.1 ableiten. Gleichwohl lässt sich ein großer Teil der euklidischen Geometrie ohne das Axiom V.2 entwickeln.

Siehe auch: Euklidischer Körper

Relative Widerspruchsfreiheit

Hilbert bewies auch, dass sein Axiomensystem widerspruchsfrei ist, wenn man unterstellt, dass sich die reellen Zahlen widerspruchsfrei begründen lassen.

Als ein Modell für das Axiomensystem dient dann, wie erwähnt, die analytische Geometrie des ${\displaystyle \mathbb {R} ^{3}}$ , also die Menge aller Tripel reeller Zahlen, zusammen mit den üblichen Definitionen für Geraden und Ebenen als lineare Punktmengen, das heißt als Nebenklassen ein- bzw. zweidimensionaler Unterräume. Die Inzidenz in diesem Modell ist das mengentheoretische Enthaltensein und zwei Strecken sind kongruent, wenn sie dieselbe Länge im Sinne des euklidischen Abstands haben.

Unabhängigkeit der Axiome untereinander

Erklärtes Ziel Hilberts war es, sein Axiomensystem so aufzubauen, dass die Axiome voneinander logisch unabhängig sind, dass also keines entbehrlich ist, weil es sich aus den anderen beweisen lässt.

Für die Axiome der Gruppe I und II untereinander lässt sich dies leicht zeigen; ebenso sind die Axiome der Gruppe III untereinander unabhängig. Es geht also darum zu zeigen, dass die Axiome der Gruppen III, IV und V von den übrigen unabhängig sind, sowie um die Unabhängigkeit von V.1 und V.2.

Das Beweisverfahren besteht grundsätzlich darin, ein Modell (oder, mit Hilberts Worten: „ein System von Dingen“) anzugeben, für das alle Axiome gelten mit Ausnahme des als unabhängig nachzuweisenden Axioms A. Offenbar könnte es ein solches Modell nicht geben, wenn A eine logische Folgerung aus den übrigen Axiomen wäre.

Auf diese Weise zeigt Hilbert u. a., dass das Axiom III.5 (der Kongruenzsatz „sws“) unentbehrlich ist.

Die Unabhängigkeit des Parallelenaxioms IV ergibt sich aus dem Nachweis der Existenz von nichteuklidischen Geometrien, die Unabhängigkeit des Archimedischen Axioms V.1 aus der Existenz von Nichtstandard-Systemen, und die Unabhängigkeit des Vollständigkeitsaxioms V.2 z. B. aus der Existenz einer analytischen Geometrie über dem Körper der reellen algebraischen Zahlen. (→ Siehe dazu auch euklidischer Körper)

Es lässt sich zeigen, dass eine Geometrie, welche diese Axiome erfüllt, bis auf Isomorphie eindeutig bestimmt ist; in der Sprache der linearen Algebra gilt für diese Geometrie:

Eine Geometrie, die Hilberts Axiomensystem erfüllt, ist ein affiner Raum, dessen Vektorraum der Verschiebungen ein dreidimensionaler euklidischer Vektorraum, also isomorph zu ${\displaystyle (\mathbb {R} ^{3},\langle \cdot ,\cdot \rangle )}$  mit einem Skalarprodukt ist.

• David Hilbert: Grundlagen der Geometrie. 14. Auflage. Teubner, Stuttgart 1999, ISBN 3-519-00237-X (Online-Kopie der Ausgabe von 1903 [abgerufen am 9. Juni 2013] Erstausgabe: 1899). 
• Benno Klotzek: Euklidische und nichteuklidische Elementargeometrien. 1. Auflage. Harri Deutsch, Frankfurt am Main 2001, ISBN 3-8171-1583-0.