Collatz-Problem: Vermutung in der Mathematik

Es hat Verbindungen zur Zahlentheorie, zur Theorie dynamischer Systeme und Ergodentheorie und zur Theorie der Berechenbarkeit in der Informatik.

Das Problem gilt als notorisch schwierig, obwohl es einfach zu formulieren ist. Jeffrey Lagarias, der als Experte für das Problem gilt, zitiert eine mündliche Mitteilung von Paul Erdős, der es als „absolut hoffnungslos“ bezeichnete.

Einleitung

 

Bei dem Problem geht es um Zahlenfolgen, die nach einem einfachen Bildungsgesetz konstruiert werden:

• Beginne mit einer beliebigen natürlichen Zahl ${\displaystyle n>0}$ .
• Ist ${\displaystyle n}$  gerade, so nimm als nächstes ${\displaystyle n/2}$ .
• Ist ${\displaystyle n}$  ungerade, so nimm als nächstes ${\displaystyle 3n+1}$ .
• Wiederhole die Vorgehensweise mit der erhaltenen Zahl.

Zum Beispiel ergibt sich mit der Startzahl ${\displaystyle n=19}$  die Folge

19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, …

Die Folge tritt somit in einen Zyklus ein, in dem die Zahlen 4, 2, 1 ständig wiederholt werden.

Die Collatz-Vermutung lautet nun:

Die Zahlenfolge mündet immer in den Zyklus 4, 2, 1, egal, mit welcher positiven natürlichen Zahl man beginnt.

Diese Vermutung wurde bislang weder bewiesen noch widerlegt.

Mathematische Formulierung der Vermutung

Formulierung der Vermutung mit Hilfe des Bildungsgesetzes

Bezeichne mit

• ${\displaystyle \mathbb {N} :=\{1,2,3,\dots \}}$  die natürlichen Zahlen ohne die Null.
• ${\displaystyle \mathbb {N} _{0}:=\{0,1,2,3,\dots \}}$  die natürlichen Zahlen mit der Null.

Sei ${\displaystyle n\in \mathbb {N} }$  und ${\displaystyle \operatorname {Col} \colon \mathbb {N} \to \mathbb {N} }$  die Collatz-Funktion

${\displaystyle \operatorname {Col} (n)={\begin{cases}{\frac {n}{2}}&{\text{wenn }}n{\text{ gerade ist,}}\\3n+1\quad &{\text{wenn }}n{\text{ ungerade ist.}}\end{cases}}}$ 

Definiere den Collatz-Orbit ${\displaystyle \forall k\in \mathbb {N} _{0}}$ 

${\displaystyle \operatorname {Col} ^{k}(n)={\begin{cases}n&{\text{wenn }}k=0,\\\operatorname {Col} (n)&{\text{wenn }}k=1,\\\operatorname {Col} (\operatorname {Col} ^{k-1}(n))\quad &{\text{wenn }}k>1.\end{cases}}}$ 

Dann lautet die Vermutung:

Zu jedem ${\displaystyle n\in \mathbb {N} }$  existiert ein ${\displaystyle r\in \mathbb {N} }$ , so dass ${\displaystyle \operatorname {Col} ^{r}(n)=1}$ .

Erläuterungen

Für den Orbit ${\displaystyle \operatorname {Col} ^{\mathbb {N} }(n)=\{n,\operatorname {Col} (n),\operatorname {Col} ^{2}(n),\operatorname {Col} ^{3}(n),\dots \}}$  gilt somit ${\displaystyle \operatorname {Col} ^{2}(n)=\operatorname {Col} (\operatorname {Col} (n))}$ , ${\displaystyle \operatorname {Col} ^{3}(n)=\operatorname {Col} (\operatorname {Col} (\operatorname {Col} (n)))}$  usw.

Um die Vermutung zu beweisen, muss man für jedes ${\displaystyle n}$  zeigen, dass ein solches ${\displaystyle r}$  existiert. Um die Vermutung zu widerlegen, muss man ein ${\displaystyle n}$  finden, für das ein solches ${\displaystyle r}$  nicht existiert.

Eine gleichwertige Aussage der Vermutung ist, dass das kleinste Element ${\displaystyle \operatorname {Col} _{\text{min}}^{\mathbb {N} }(n)=\inf _{r\in \mathbb {N} }\operatorname {Col} ^{r}(n)}$  jedes Collatz-Orbits die Zahl ${\displaystyle 1}$  ist.

Preisgeld für die Lösung

Trotz zahlreicher Anstrengungen gehört diese Vermutung noch immer zu den ungelösten Problemen der Mathematik. Mehrfach wurden Preise für eine Lösung ausgelobt:

• 1970 bot H. S. M. Coxeter 50 Dollar für einen Beweis der Vermutung und 100 Dollar für ein Gegenbeispiel.
• 1982 versprach Bryan Thwaites in der Zeitung The Times 1000 Pfund für einen Beweis oder eine Widerlegung (Angebot 1996/1998 erneuert).
• Paul Erdős bot angeblich 500 Dollar für eine Lösung und sagte über das Collatz-Problem:

„Mathematics is not yet ready for such problems.“ („Die Mathematik ist für solche Probleme noch nicht bereit.“) und
„Hopeless. Absolutely hopeless.“ („Hoffnungslos. Absolut hoffnungslos.“)

Der Mathematiker Richard Guy warnte 1983 vor diesem und drei anderen auch heute noch ungelösten Problemen:

„Don’t try to solve these problems!“ („Versuche nicht, diese Probleme zu lösen!“)

Der Ursprung der Collatz-Vermutung liegt insofern etwas im Nebel, als aus der mutmaßlichen Entstehungszeit bisher keine schriftlichen Dokumente mit einer Beschreibung des Problems öffentlich zugänglich sind. Es wird berichtet, dass Collatz das Problem beim Internationalen Mathematikerkongress 1950 in Cambridge (Massachusetts) mündlich verbreitete. Stanisław Ulam und Shizuo Kakutani, die auf diesem Kongress zu Vorträgen eingeladen waren, stellten das Problem immer wieder in Gesprächen dar und werden deshalb in diesem Zusammenhang häufig genannt. Als Lothar Collatz 1952 seine Professur in Hamburg antrat, erzählte er seinem Hamburger Kollegen Helmut Hasse von der Vermutung. Dieser verbreitete das Problem während eines Forschungsaufenthalts an der Syracuse University, deshalb erhielt das Collatz-Problem auch den Namen Syracuse-Vermutung. Publikationen zur Entstehung und Verbreitung:

• 1971 wurde das Collatz-Problem in der gedruckten Version eines 1970 gehaltenen Vortrags von H. S. M. Coxeter zum vermutlich ersten Mal schriftlich veröffentlicht.
• 1972 erfuhr Martin Gardner von der Beschäftigung der akademischen Hacker am MIT mit dem (3n+1)-Problem und beschrieb es in seiner Kolumne Mathematical Games im Scientific American. Die Vermutung wurde durch diese und weitere Veröffentlichungen unter anderem von John Conway inner- und außerhalb von Fachkreisen weithin bekannt.
• 1976 veröffentlichte Riho Terras die ersten wissenschaftlichen Forschungsergebnisse direkt zum Collatz-Problem. Terras zeigte mit probabilistischen Methoden, dass

${\displaystyle \operatorname {Col} _{\text{min}}^{\mathbb {N} }(n)$ 
für fast alle (bezüglich der logarithmischen Dichte) ${\displaystyle n\in \mathbb {N} }$  gilt.

• 1985 erschien in der Zeitschrift American Mathematical Monthly ein Überblicksartikel von Jeffrey Lagarias. Lagarias berichtet darin über Collatz’ Interesse an zahlentheoretischen Funktionen und Graphentheorie, und er zitiert einen Notizbucheintrag vom 1. Juli 1932, in dem Collatz die folgende Permutation der positiven ganzen Zahlen betrachtet:

${\displaystyle g(n)={\begin{cases}{\tfrac {2}{3}}n&{\text{wenn}}\quad n\equiv 0\mod 3,\\{\tfrac {4}{3}}n-{\tfrac {1}{3}}&{\text{wenn}}\quad n\equiv 1\mod 3,\\{\tfrac {4}{3}}n+{\tfrac {1}{3}}&{\text{wenn}}\quad n\equiv 2\mod 3.\end{cases}}}$ 
Diese Permutation besitzt den Fixpunkt 1 und außerdem zumindest die Zyklen (2, 3), (4, 5, 7, 9, 6) und (44, 59, 79, 105, 70, 93, 62, 83, 111, 74, 99, 66). In dem zitierten Notizbucheintrag stellt Collatz die auch heute noch offene Frage, ob die mit 8 beginnende g-Trajektorie zyklisch wird oder gegen unendlich divergiert. Die ebenfalls weiterhin offene Frage, ob weitere Zyklen existieren, ist wie die (3n+1)-Vermutung eines der von Guy beschriebenen Probleme, die man nicht zu lösen versuchen solle.

• 1985 veröffentlichte Bryan Thwaites eine Mitteilung, er habe die Vermutung am 21. Juli 1952 um vier Uhr nachmittags als Aufgabe zur Unterhaltung seiner Schüler gestellt (er beanspruchte bereits 1982 die Entdeckung im Jahr 1952).
• 1986 ließ Lothar Collatz eine Darstellung seines Entdeckungswegs zur (3n+1)-Vermutung ins Chinesische übersetzen und in einem Journal der Pädagogischen Universität Qufu, Shandong, China, an der er einen Vortrag darüber gehalten hatte, veröffentlichen. Dies blieb die einzige Veröffentlichung von Collatz zu diesem Problem.

Nach Terras’ Publikation 1976 begann nach und nach eine rege wissenschaftliche Beschäftigung mit dem Collatz-Problem, die mittlerweile weit mehr als hundert Publikationen mit neuen Forschungsergebnissen umfasst. Im populärwissenschaftlichen Bereich entstanden neue Bezeichnungen:

• 1979 nannte Douglas R. Hofstadter in seinem Buch Gödel, Escher, Bach diejenigen Startzahlen, deren Collatz-Trajektorie im Zyklus (1,4,2) endet, wondrous numbers, wundersame Zahlen.
• 1984 nannte Brian Hayes die Zahlen von Collatz-Folgen in der Kolumne Computer recreations im Scientific American hailstone numbers, Hagelschlagzahlen.
• 1994 zeigte Ivan Korec, dass für die Anfangswerte ${\displaystyle S}$  fast überall für den Collatz-Algorithmus einen Wert unter ${\displaystyle S^{0,7925}}$  erreichen.
• 2019 zeigte Terence Tao, dass die Collatz-Vermutung für die natürlichen Zahlen fast zutrifft, siehe Abschnitt Collatz-Problem#Teillösung von Tao. Tao nützte dabei probabilistische Methoden und zeigte mittels der logarithmischen Dichte, dass das Infimum des Collatz-Orbits für die Elemente fast überall für jede divergierende Funktion beschränkt ist, egal wie langsam diese divergiert (zum Beispiel ${\displaystyle \log \log \log \log n}$ ).

 

Collatz’ Beschreibung seiner Motivation der (3n+1)-Vermutung ist sehr plausibel: Er assoziiert zunächst ganz allgemein zu einer beliebigen Funktion auf den natürlichen Zahlen mit Werten in den natürlichen Zahlen einen gerichteten Graphen, der von Lagarias im oben erwähnten Überblicksartikel Collatz-Graph genannt wird. Der Collatz-Graph einer zahlentheoretischen Funktion

${\displaystyle f\colon \mathbb {N} \to \mathbb {N} }$ 

ist ein gerichteter Graph, bestehend aus der Menge der natürlichen Zahlen als Knotenmenge und zu jeder natürlichen Zahl ${\displaystyle n}$  einer gerichteten Kante von ${\displaystyle n}$  nach ${\displaystyle f(n)}$ .

Die einfachste solche Funktion ist die Nachfolgerabbildung

${\displaystyle s\colon \mathbb {N} \to \mathbb {N} ,\quad s(n)=n+1,}$ 

deren Collatz-Graph aus einem unendlich langen Weg besteht:

${\displaystyle 1\to 2\to 3\to 4\to 5\to \dotsb }$ 

Um mehr Beispiele zu haben, suchte er zunächst nach einer möglichst „einfachen“ zahlentheoretischen Funktion, deren Collatz-Graph einen Kreis enthält. Eine solche Funktion ${\displaystyle f}$  muss auf gewissen natürlichen Zahlen ${\displaystyle n}$  „aufsteigen“, also die Relation ${\displaystyle n$  erfüllen, und auf anderen natürlichen Zahlen ${\displaystyle m}$  „absteigen“, also die Relation ${\displaystyle m>f(m)}$  erfüllen. So stieß er zunächst auf die Funktion, die definiert ist durch

${\displaystyle C_{1}(n):={\begin{cases}n/2&{\text{wenn }}n{\text{ gerade ist,}}\\n+1\quad &{\text{wenn }}n{\text{ ungerade ist.}}\end{cases}}}$ 

Den Collatz-Graphen dieser Funktion kann man wie folgt beschreiben: Die Knoten sind, nach Definition, die positiven ganzen Zahlen. Ist der Knoten ${\displaystyle k}$  gerade, besitzt ${\displaystyle k}$  die beiden Vorgängerknoten ${\displaystyle k-1}$  und ${\displaystyle 2k}$ , sonst nur ${\displaystyle 2k}$ . Außerdem gilt

${\displaystyle C_{1}^{2}(n)=C_{1}(C_{1}(n))={\begin{cases}{\frac {n}{4}}&{\text{wenn }}n{\text{ durch 4 teilbar ist,}}\\{\frac {n}{2}}+1&{\text{wenn }}n{\text{ durch 2, aber nicht durch 4 teilbar ist,}}\\{\frac {n+1}{2}}\quad &{\text{wenn }}n{\text{ ungerade ist.}}\end{cases}}}$ 

Daraus folgt

${\displaystyle C_{1}^{2}(n)2,}$ 

und das hat zur Folge, dass der Collatz-Graph von ${\displaystyle C_{1}}$  nur den Kreis ${\displaystyle (1,2)}$  besitzt und dass die ${\displaystyle C_{1}}$ -Trajektorie zu jeder beliebigen Startzahl in diesen Kreis mündet.

Weil diese Argumentation ziemlich einfach ist, suchte Collatz weiter: Der Collatz-Graph der Funktion

${\displaystyle C_{2}(n)={\begin{cases}n/2&{\text{wenn }}n{\text{ gerade ist,}}\\2n+1\quad &{\text{wenn }}n{\text{ ungerade ist,}}\end{cases}}}$ 

enthält keinen Kreis, da jede ungerade Zahl auf eine größere ungerade Zahl abgebildet wird, und die ${\displaystyle C_{2}}$ -Trajektorien daher alle gegen unendlich divergieren.

Der nächste Versuch ist die Collatz-Funktion

${\displaystyle C\colon \mathbb {N} \to \mathbb {N} ,\quad C(n)={\begin{cases}n/2&{\text{wenn }}n{\text{ gerade ist,}}\\3n+1&{\text{wenn }}n{\text{ ungerade ist.}}\end{cases}}}$      (Folge A006370 in OEIS)

Zu dieser Funktion fand Collatz nur den „trivialen Kreis“ ${\displaystyle (1,4,2)}$  – er schrieb, er habe seine Ideen deshalb nicht veröffentlicht, weil er nicht beweisen konnte, dass der „triviale Kreis“ der einzige sei. Die Collatz-Vermutung ist in graphentheoretischer Formulierung die Vermutung, dass der Collatz-Graph von ${\displaystyle C}$  zusammenhängend ist.

 

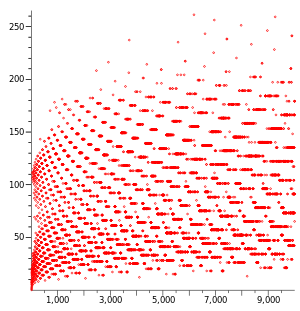
Für eine ${\displaystyle C}$ -Trajektorie als Zahlenfolge kann man drei einander ausschließende Fälle unterscheiden:

• die Folge endet im (1,4,2)-Zyklus,
• die Folge wächst über alle Grenzen,
• die Folge gerät in einen anderen Zyklus.

Die Vermutung besagt, dass nur der erste Fall eintritt, aber weder der zweite noch der dritte Fall konnte bisher ausgeschlossen werden. Es ist auch nicht bekannt, ob es nur endlich viele Zyklen geben kann.

Da ${\displaystyle 3n+1}$  für ungerade ${\displaystyle n}$  stets gerade ist und somit die folgende Iteration immer die Division durch 2, wird statt der Collatz-Funktion ${\displaystyle C}$  meistens die etwas einfacher zu handhabende Funktion

${\displaystyle T\colon \mathbb {N} \to \mathbb {N} ,\quad T(n)={\begin{cases}n/2&{\text{wenn }}n{\text{ gerade ist,}}\\(3n+1)/2&{\text{wenn }}n{\text{ ungerade ist,}}\end{cases}}}$      (Folge A014682 in OEIS)

verwendet, die also für ungerade ${\displaystyle n}$  zwei ${\displaystyle C}$ -Iterationen auf einmal macht und den der Vermutung zufolge stets erreichten Zyklus von (1,4,2) auf (1,2) reduziert. Die ${\displaystyle k}$ -fache Abbildung ${\displaystyle T^{k}}$  bildet ${\displaystyle 2^{k}m}$  auf ${\displaystyle m}$  und ${\displaystyle 2^{k}m-1}$  auf ${\displaystyle 3^{k}m-1}$  ab, insbesondere gibt es für jeden beliebig großen Faktor Startwerte, die die wiederholte Abbildung mit ${\displaystyle C}$  oder ${\displaystyle T}$  um mindestens diesen Faktor vergrößert. Die Collatz-Vermutung ist äquivalent zu der Vermutung, dass für alle ganzen Zahlen ${\displaystyle n>1}$  eine ganze Zahl ${\displaystyle k>0}$  mit ${\displaystyle T^{k}(n)$  existiert. Terras zeigte 1976, dass die asymptotische Dichte der ganzen Zahlen ${\displaystyle n>1}$ , für die das zutrifft, existiert und gleich 1 ist.

Berechnungen mit Computern ergaben:

• Alle positiven ganzen Zahlen bis 2⁶⁸ (ca. 2,95×10²⁰) als Startwerte bestätigen die Vermutung (Stand Juli 2020).
• Hat die ${\displaystyle T}$ -Iteration noch einen anderen Zyklus als (1,2), dann muss dieser aus mindestens 10.439.860.591 Zahlen bestehen, davon mindestens 6.586.818.670 ungerade.
• Für unendlich viele positive ganze Zahlen ${\displaystyle n}$  sind mindestens 6,143 log n Iterationen mit ${\displaystyle T}$  erforderlich, um 1 zu erreichen. Stochastische Modelle sagen voraus, dass durchschnittlich (2 / log(4/3)) log n ≈ 6,952 log n Schritte benötigt werden und dass für mindestens die Hälfte aller Zahlen mindestens so viele ${\displaystyle T}$ -Iterationen erforderlich sind.
• Für genügend große ${\displaystyle X}$  ist die Anzahl der positiven ganzen Zahlen kleiner oder gleich ${\displaystyle X}$ , die als Startwert die Vermutung bestätigen, mindestens ${\displaystyle X^{0{,}84}}$ .

 

Terence Tao zeigte 2019, dass die Collatz-Vermutung für „fast alle“ natürlichen Zahlen „fast“ zutrifft (das heißt, man endet mit der Collatzfolge „nahe“ 1, wobei die Schranke für die Nähe vom Startwert N abhängt). Beispielsweise folgt aus Taos Satz, dass mindestens 99 Prozent der natürlichen Zahlen bis ${\displaystyle 10^{24}}$ , mit denen man die Collatzfolge startet, einen Endwert erreichen, der unter 200 liegt. Tao benutzte dabei Methoden, die er zuvor in der Theorie partieller Differentialgleichungen angewandt hatte, indem er statistisch eine Auswahl von Anfangswerten sampelte und dann das „Langzeitverhalten“ des Ensembles unter der Collatztransformation untersuchte.

Grundlegende Eigenschaften der Folgen

Betrachtet man bei der Anwendung der Collatz-Funktion nur ungerade Zahlen, kann man mit elementaren Rechnungen einige grundlegende Eigenschaften dieser Abbildung zeigen.

Ungerade natürliche Zahlen haben bei einer Division durch 4 entweder den Rest 1 oder den Rest 3. Die ungeraden natürlichen Zahlen lassen sich so in zwei disjunkte Teilmengen aufteilen. Die eine Teilmenge der ungeraden Zahlen sind die Zahlen der Reihe 4n+1 mit ${\displaystyle n\in \mathbb {N} _{0}}$ . Die andere Teilmenge sind die Zahlen der Reihe 4n+3 mit ${\displaystyle n\in \mathbb {N} _{0}}$ . Wendet man nun auf die Zahlen der ersten Reihe die Collatz-Funktion an, erhält man die Zahlen der Reihe 12n+4. Da es sich bei diesen Zahlen immer um gerade Zahlen handelt, kann die Collatz-Funktion erneut angewendet werden. Die Zahlen der Reihe 12n+4 werden also auf die Zahlen der Reihe 6n+2 abgebildet und diese dann auf die Zahlen der Reihe 3n+1. Durch weitere Rechnungen in dieser Art lassen sich die folgenden allgemeinen Eigenschaften der Orbits zeigen:

• Beschränkt man sich bei der Zielmenge der Collatz-Funktion oder Teilmengen davon auch auf die ungeraden natürlichen Zahlen, so sind die Zahlen dieser Mengen nach den ersten zwei Anwendungen der Collatz-Funktion (zwei Iterationen) weder durch 2 noch durch 3 teilbar.

• Die ungeraden Zahlen der Reihe 4n+1 mit ${\displaystyle n\in \mathbb {N} _{0}}$  werden nach drei Iterationen auf die kleineren Zahlen der Reihe 3n+1 abgebildet.

• Die Zahlen der Reihe 4n+3 mit ${\displaystyle n\in \mathbb {N} _{0}}$  werden in den zwei folgenden Iterationen auf die größeren und ungeraden Zahlen der Reihe 6n+5 abgebildet. Nach zwei weiteren Iterationen werden diese Zahlen dann auf die Zahlen der Reihe 9n+8 abgebildet. Die Zahlen der Reihe 9n+8 sind abwechselnd gerade und ungerade.

• Die Zahlen der Reihe 8n+3 mit ${\displaystyle n\in \mathbb {N} _{0}}$  werden nach fünf Iterationen auf die Zahlen der Reihe 9n+4 abgebildet

• Aufgrund der oben genannten Eigenschaften ist es bei einer Überprüfung der Collatz-Vermutung für alle natürlichen Zahlen unterhalb einer Schranke ${\displaystyle M}$  mit ${\displaystyle M\in \mathbb {N} }$  hinreichend, sich auf die Zahlen der Reihe 4n+3, die kleiner oder gleich ${\displaystyle M}$  sind, zu beschränken.

Die genannten Regeln können dazu benutzt werden, um bei einer Überprüfung der Collatz-Vermutung für alle natürlichen Zahlen unterhalb einer gegebenen Schranke mit Hilfe von Computerprogrammen Rechenzeit einzusparen.

In ähnlicher Weise lässt sich auch die etwas allgemeinere Formel herleiten:

${\displaystyle T^{k}(2^{k}n+a)=3^{c(a,k)}n+d(a,k)}$ .

Mit Hilfe der Konstanten ${\displaystyle c(a,k)}$  und ${\displaystyle d(a,k)}$  und der genannten Formel kann man somit ohne Ausführung der ${\displaystyle T}$ -Iterationen das Ergebnis von k Iterationen direkt berechnen. Dabei bezeichnet die Konstante ${\displaystyle c(a,k)}$  die Anzahl aller ungeraden Zahlen, die sich während dieser ${\displaystyle T}$ -Iterationen ergibt. Diese Anzahl hängt nur von den zwei Konstanten ${\displaystyle k}$  und ${\displaystyle a}$  ab. Die Konstante ${\displaystyle d(a,k)}$  ist das Ergebnis von k ${\displaystyle T}$ -Iterationen angewendet auf die Zahl ${\displaystyle a}$ . So lässt sich bei der Verwendung von Computerprogrammen ebenfalls Rechenzeit einsparen. Für ${\displaystyle k=2}$  ergeben sich die folgenden Werte für die beiden benötigten Konstanten

${\displaystyle {\begin{aligned}c(0\ldots 3,2)&=\{0,1,1,2=k\}\\d(0\ldots 3,2)&=\{0,1,2,8=3^{k}-1\}\end{aligned}}}$ 

Für ${\displaystyle k=5}$  ergeben sich die folgenden Werte:

${\displaystyle {\begin{aligned}c(0\ldots 31,5)&=\{0,3,2,2,2,2,2,4,1,4,1,3,2,2,3,4,1,2,3,3,1,1,3,3,2,3,2,4,3,3,4,5=k\}\\d(0\ldots 31,5)&=\{0,2,1,1,2,2,2,20,1,26,1,10,4,4,13,40,2,5,17,17,2,2,20,20,8,22,8,71,26,26,80,242=3^{k}-1\}\end{aligned}}}$ 

Beispiele zu obiger Formel sind:

• Für ${\displaystyle 2^{5}n+1}$  ergeben sich bei 5 ${\displaystyle T}$ -Iterationen immer 3 ungerade Zahlen. 1 iteriert dabei zu 2, 1, 2, 1, 2. Somit ergibt sich ${\displaystyle 3^{3}n+2}$ .
• Für ${\displaystyle 2^{2}n+1}$  ergibt sich bei den zwei Iterationen nur eine ungerade Zahl. 1 iteriert zu 2 und dann zu 1. Damit ergibt sich, wie bereits weiter oben gezeigt, das Ergebnis ${\displaystyle 3n+1}$ .
• Für ${\displaystyle 2^{k}n-1}$  ergeben sich ${\displaystyle k}$  ungerade Zahlen. Das Ergebnis lautet dann ${\displaystyle 3^{k}n-1}$ .
• Für ${\displaystyle 2^{k}n+1}$  ergibt sich bei ungeradem ${\displaystyle k}$  nach ${\displaystyle k}$  ${\displaystyle T}$ -Iterationen ${\displaystyle 3^{(k+1)/2}n+2}$ .
• Für ${\displaystyle 2^{k}n+1}$  ergibt sich bei geradem ${\displaystyle k}$  nach ${\displaystyle k}$  ${\displaystyle T}$ -Iterationen ${\displaystyle 3^{k/2}n+1}$ .

Die letzten drei Beispiele zeigen, dass es für den Maximalwert der Collatz-Folgen keine obere Schranke gibt. Ebenso gibt es demnach auch keine obere Schranke für die Länge einer Collatz-Folge.

Die Syracuse-Funktion (benannt nach der Syracuse University in New York) ist eine mit der Collatz-Funktion verwandte Funktion. Sei ${\displaystyle n\in \mathbb {N} }$ , falls ${\displaystyle n}$  eine ungerade Zahl ist, dann ist ${\displaystyle 3n+1}$  gerade und besitzt eine Primfaktorzerlegung der Form

${\displaystyle 2^{a}p_{1}^{e_{1}}\cdots p_{s}^{e_{s}}=2^{a}k}$ 

wobei ${\displaystyle a\in \mathbb {N} }$  und ${\displaystyle k}$  die größte ungerade Zahl ist, welche ${\displaystyle 3n+1}$  ohne Rest teilt. Sei ${\displaystyle 2\mathbb {N} +1:=\{1,3,5,\dots \}}$  die Menge der ungeraden Zahlen, dann ist die Syracuse-Funktion ${\displaystyle \operatorname {Syr} :2\mathbb {N} +1\to 2\mathbb {N} +1}$  die Funktion

${\displaystyle \operatorname {Syr} (n):={\frac {3n+1}{2^{a}}}=k.}$ 

Beispielsweise gilt ${\displaystyle \operatorname {Syr} (3)=5}$ , ${\displaystyle \operatorname {Syr} (5)=1}$  und ${\displaystyle \operatorname {Syr} (7)=11}$ .

Für eine Primzahl ${\displaystyle p}$  und ${\displaystyle M\in \mathbb {Z} }$  sei ${\displaystyle \nu _{p}(M)}$  die ${\displaystyle p}$ -Bewertung, das heißt die größte Zahl ${\displaystyle a}$ , so dass ${\displaystyle p^{a}\mid M}$ , mit der Konvention ${\displaystyle \nu _{p}(0)=+\infty }$ . Dann lässt sich ${\displaystyle \operatorname {Syr} (n)}$  auch wie folgt ausdrücken

${\displaystyle \operatorname {Syr} (n):={\frac {3n+1}{2^{\nu _{2}(3n+1)}}}.}$ 

Analog zur Collatz-Funktion lässt sich nun auch der Syracuse-Orbit ${\displaystyle \operatorname {Syr} ^{\mathbb {N} }}$  und sein Minimal-Element ${\displaystyle \operatorname {Syr} _{\text{min}}^{\mathbb {N} }}$  definieren.

Die Syracuse-Funktion spielt eine zentrale Rolle in Taos Beweis.

2019 bewies Tao folgenden Satz:

Sei ${\displaystyle f:\mathbb {N} +1\to \mathbb {R} }$  eine Funktion mit ${\displaystyle \lim \limits _{N\to \infty }f(N)=+\infty }$ . Dann gilt ${\displaystyle \operatorname {Col} _{\text{min}}^{\mathbb {N} }(N)$  für fast alle ${\displaystyle N\in \mathbb {N} +1}$ .

Tao nützte folgende Notation für die natürlichen Zahlen:

• mit der Null als ${\displaystyle \mathbb {N} :=\{0,1,2,\dots \}}$ 
• ohne Null als ${\displaystyle \mathbb {N} +1:=\{1,2,\dots \}}$ 
• an ungerader Stelle ${\displaystyle 2\mathbb {N} +1:=\{1,3,5,\dots \}}$ 

Die Bezeichnung fast alle bezeichnet eine Eigenschaft bezüglich der logarithmischen Dichte. Eine schwächere Form als die asymptotische Dichte.

Erläuterungen

Logarithmische Dichte:

Sei ${\displaystyle R\subset \mathbb {N} +1}$  eine nicht leere endliche Teilmenge. Wir definieren die Zufallsvariable ${\displaystyle \mathbf {Log} (R)}$ , welche Werte in ${\displaystyle R}$  annimmt und der logarithmischen Gleichverteilung folgt, das heißt, für alle ${\displaystyle A\subset \mathbb {N} +1}$  gilt

${\displaystyle \mathbb {P} (\mathbf {Log} (R)\in A)={\frac {\sum _{N\in A\cap R}{\frac {1}{N}}}{\sum _{N\in R}{\frac {1}{N}}}}.}$ 

Die logarithmische Dichte von ${\displaystyle A\subset \mathbb {N} }$  ist dann definiert als der Grenzwert

${\displaystyle \lim \limits _{x\to \infty }\mathbb {P} (\mathbf {Log} (\mathbb {N} +1\cap [1,x])\in A),}$ 

sofern dieser existiert.

Die logarithmische Dichte von ${\displaystyle A}$  ist somit die Wahrscheinlichkeit, dass sich der Grenzwert der Zufallsvariable ${\displaystyle \mathbf {Log} (\mathbb {N} +1\cap [1,x])}$  in der Menge ${\displaystyle A}$  befindet.

Beispiele:

• Sei ${\displaystyle A:=\{2,4,6,8,10\dots \}}$  und ${\displaystyle R_{x}:=\mathbb {N} +1\cap [1,x]}$ . Dann ist

${\displaystyle \lim \limits _{x\to \infty }\mathbb {P} (\mathbf {Log} (R_{x})\in A)=\lim \limits _{x\to \infty }{\frac {\sum _{N\in A\cap R_{x}}{\frac {1}{N}}}{\sum _{N\in R_{x}}{\frac {1}{N}}}}={\frac {\sum _{N\in A}{\frac {1}{N}}}{\sum _{N\in \mathbb {N} +1}{\frac {1}{N}}}}={\frac {{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{6}}+{\frac {1}{8}}+{\frac {1}{10}}+\cdots }{1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }}={\frac {1}{2}}}$ 

Fast alle:

Eine Eigenschaft ${\displaystyle P(N)}$  gilt für fast alle ${\displaystyle N\in \mathbb {N} +1}$ , falls

${\displaystyle \lim \limits _{x\to \infty }\mathbb {P} (P(\mathbf {Log} (\mathbb {N} +1\cap [1,x])))=1.}$ 

In Worten ausgedrückt ${\displaystyle P(N)}$  gilt in einer Teilmenge ${\displaystyle N\subset \mathbb {N} +1}$  mit logarithmischer Dichte ${\displaystyle 1}$ .

Beweis-Idee

Der Satz wird für ${\displaystyle \operatorname {Syr} _{\text{min}}^{\mathbb {N} }(N)}$  bewiesen und der Fall für ${\displaystyle \operatorname {Col} _{\text{min}}^{\mathbb {N} }}$  folgt daraus, denn es gilt

${\displaystyle \operatorname {Col} _{\text{min}}^{\mathbb {N} }(N)=\operatorname {Syr} _{\text{min}}^{\mathbb {N} }(N/2^{\nu _{2}(N)})}$ .

Wir definieren:

• Für ein ${\displaystyle a\in \mathbb {N} +1}$  und ${\displaystyle x\in \mathbb {R} }$  die affine Abbildung

${\displaystyle \operatorname {Aff} _{a}(x):={\tfrac {3x+1}{2^{a}}}.}$ 

• Für ein ${\displaystyle n}$ -Tupel ${\displaystyle (a_{1},\dots ,a_{n})\in (\mathbb {N} +1)^{n}}$  die Komposition

${\displaystyle \operatorname {Aff} _{(a_{1},\dots ,a_{n})}(x):=\operatorname {Aff} _{a_{n}}(\operatorname {Aff} _{a_{n-1}}(\dots (\operatorname {Aff} _{a_{1}}(x))\dots ))}$ .

• Die ${\displaystyle n}$ -Syracuse-Bewertung ${\displaystyle {\vec {a}}^{(n)}(N)\in (\mathbb {N} +1)^{n}}$  als

${\displaystyle {\vec {a}}^{(n)}(N):=\left(\nu _{2}(3N+1),\nu _{2}(3\operatorname {Syr} (N)+1),\dots ,\nu _{2}(3\operatorname {Syr} ^{n-1}(N)+1)\right).}$ 

Daraus folgt ${\displaystyle \operatorname {Syr} (N)=\operatorname {Aff} _{\nu _{2}(3N+1)}(N)}$  und ${\displaystyle \operatorname {Syr} ^{n}(N)=\operatorname {Aff} _{{\vec {a}}^{(n)}(N)}(N)}$ .

Weiter definieren wir die geometrische Zufallsvariable ${\displaystyle \operatorname {Geom} (\mu )}$  mit Erwartungswert ${\displaystyle \mu >1}$ , so dass für alle ${\displaystyle a\in \mathbb {N} +1}$  gilt

${\displaystyle \mathbb {P} (\operatorname {Geom} (\mu )=a)={\frac {1}{\mu }}\left({\frac {\mu -1}{\mu }}\right)^{a-1}.}$ 

Für ein zufälliges ${\displaystyle N\in 2\mathbb {N} +1}$  kann die Anzahl, wie oft ${\displaystyle 3N+1}$  durch ${\displaystyle 2}$  geteilt werden kann, als geometrische Zufallsvariable mit Erwartungswert ${\displaystyle 2}$  interpretiert werden:

${\displaystyle \mathbb {P} (\operatorname {Geom} (2)=a)=2^{-a}.}$ 

Es lässt sich folgende Heuristik herleiten: Falls ${\displaystyle N}$  eine spezielle große, ungerade Zahl ist und ${\displaystyle n\ll \log N}$  (bedeutet ${\displaystyle n}$  ist viel kleiner als ${\displaystyle \log N}$ ), dann verhält sich ${\displaystyle {\vec {a}}^{(n)}(N)}$  wie die Zufallsvariable ${\displaystyle \operatorname {Geom} (2)^{n}}$ . Genauer: Definiere die diskrete totale Variation zweier Zufallsvariablen auf einer diskreten Menge ${\displaystyle R}$  als

${\displaystyle d_{TV}(X,Y):=\sum \limits _{r\in R}|\mathbb {P} (X=r)-\mathbb {P} (Y=r)|.}$ 

Nun lässt sich eine obere Schranke für die totale Variation von ${\displaystyle {\vec {a}}^{(n)}(N)}$  und ${\displaystyle \operatorname {Geom} (2)^{n}}$  finden:

${\displaystyle d_{TV}\left({\vec {a}}^{(n)}(N),\operatorname {Geom} (2)^{n}\right)\ll 2^{-c_{1}n},}$ 

wobei ${\displaystyle c_{1}>0}$  eine Konstante bezeichnet. Da man nun sehr viel über die Verteilung von ${\displaystyle {\vec {a}}^{(n)}(N)}$  weiß, lassen sich endliche Stoppzeiten für ${\displaystyle \operatorname {Syr} ^{\mathbb {N} }}$  herleiten.

Da eine Division und Multiplikation von natürlichen Zahlen im Dualsystem besonders einfach durchzuführen ist, kann die Collatz-Funktion auch als eine abstrakte Maschine verstanden werden, die Zeichenketten von Bits verarbeitet. Die Maschine wendet die folgenden drei Regeln auf eine beliebige ungerade Zahl ${\displaystyle n}$  im Dualsystem an:

1. Füge rechts an die Binärzahl eine Eins an. Das ergibt 2n + 1.
2. Addiere die Zahl aus dem ersten Schritt zur ursprünglichen Zahl. Das ergibt dann n + 2n + 1 = 3n + 1.
3. Entferne alle Nullen am rechten Rand der neuen Zahl. Das entspricht so vielen Divisionen durch 2, bis das Resultat wieder eine ungerade Zahl ist.

Beispiel

Man startet mit der dezimalen 7 (binär 111). Der resultierende Collatz-Orbit lautet dann:

         111         1111        10110       10111      100010     100011     110100    11011   101000  1011 10000 

Für das auf alle ganzen Zahlen als Startwerte ausgeweitete Collatz-Problem gibt es außer dem (1,4,2)-Zyklus noch mindestens vier weitere Zyklen:

(0),
(−1, −2),
(−5, −14, −7, −20, −10)  und
(−17, −50, −25, −74, −37, −110, −55, −164, −82, −41, −122, −61, −182, −91, −272, −136, −68, −34).

Die drei letzten Zyklen mit positiven statt negativen Vorzeichen entstehen auch mit der Definition ${\displaystyle C(n)=3n-1}$  statt ${\displaystyle C(n)=3n+1}$  für ungerade ${\displaystyle n}$ . Alle Startwerte ${\displaystyle n}$  mit ${\displaystyle |n|<10^{8}}$  enden in einem der bekannten Zyklen.

Marc Chamberland definierte eine stetige Funktion, welche die diskrete Collatz-Folge auf den Bereich der reellen Zahlen erweitert. Simon Letherman, Dierk Schleicher und Reg Wood betrachteten Funktionen im Bereich der komplexen Zahlen als Erweiterung. Allgemeine Vermutung: ${\displaystyle C(n)=3n+3^{x}}$  für ungerade ${\displaystyle n}$  endet immer in ${\displaystyle (4\cdot 3^{x},2\cdot 3^{x},1\cdot 3^{x})}$  und besitzt nur diesen einen Zyklus.

Betrachtet man das analoge (5n+1)-Problem, so liefern stochastische Modelle ein ganz anderes Verhalten: Fast alle Iterierten sollten divergieren, was durch Computersimulation bestätigt wird. Es ist aber ein offenes Problem zu beweisen, dass auch nur ein Orbit des (5n+1)-Problems tatsächlich divergiert.

John Conway betrachtete 1972 verallgemeinerte (3n+1)-Folgen und zeigte, dass sie universale Turingmaschinen simulieren können (von ihm in der Programmiersprache FRACTRAN verallgemeinert). Außerdem zeigte er, dass ein bestimmtes Entscheidungsproblem unlösbar ist, das danach fragt, ob ein Eingangswert für die Iteration, der eine Potenz von 2 ist, zu einem iterierten Wert führt, der ebenfalls eine Potenz von 2 ist (das Collatz-Problem lässt sich auch so formulieren, dass für beliebige natürliche Zahlen als Input die Iterierte schließlich auf eine Potenz von 2 führt).

In ihrer 2020 veröffentlichten Arbeit analysieren Sultanow, Koch und Cox das Collatz-Problem aus graphentheoretischer Sicht. Sie betrachten Zyklen für ${\displaystyle 3n+1}$  und die verallgemeinerte Form ${\displaystyle kn+1}$ , wobei ${\displaystyle k\in \mathbb {N} _{>0}}$ . Das Dokument beinhaltet eine Liste bekannter Zyklen und leitet daraus Bedingungen für deren Auftreten in Collatz-Sequenzen ab.

• Jeffrey C. Lagarias: The 3x+1 problem and its generalizations, The American Mathematical Monthly 92, Januar 1985, S. 3–23 (englisch; 1986 mit dem Lester-R.-Ford-Preis ausgezeichnet; bei MathDL; beim CECM; Zentralblatt-Rezension)
• Günther J. Wirsching: The dynamical system generated by the 3n+1 function, Springer-Verlag, Berlin 1998, ISBN 3-540-63970-5 (englisch; revidierte Version der Habilitationsschrift von 1996; Zentralblatt-Rezension)
• Richard K. Guy: E16. The 3x+1 problem und E17. Permutation sequences in Unsolved problems in number theory (3. Auflage), Springer-Verlag, New York 2004, ISBN 0-387-20860-7, S. 330–336 und S. 336–337 (englisch; Zentralblatt-Rezension)
• Jeffrey C. Lagarias: The 3x+1 problem: An annotated bibliography (1963–1999) (sorted by author), arxiv:math/0309224 [math.NT], 2003–2011 (englisch)
• Jeffrey C. Lagarias: The 3x+1 problem: An annotated bibliography, II (2000–2009), arxiv:math/0608208 [math.NT], 2006–2012 (englisch)
• Jeffrey C. Lagarias (Hrsg.): The ultimate challenge: The 3x+1 problem, American Mathematical Society, Providence RI 2010, ISBN 978-0-8218-4940-8 (englisch; Zentralblatt-Rezension)
  • darin Jeffrey C. Lagarias: The 3x+1 problem: An overview (PDF, 518 kB, Buchvorschau), S. 3–29 (englisch)

 

Wikibooks: Collatzfolgen und Schachbrett – Lern- und Lehrmaterialien

 

Commons: Collatz-Problem – Sammlung von Bildern, Videos und Audiodateien

• Eric W. Weisstein: Collatz Problem. In: MathWorld (englisch).
• On the 3x + 1 problem von Eric Roosendaal, ein Distributed-computing-Projekt, das sich mit dem Collatz-Problem beschäftigt (englisch)
• Collatz Conjecture von Jon Sonntag, ein auf BOINC basierendes Projekt, das sich mit der Suche nach Gegenbeispielen beschäftigt (englisch; siehe Collatz Conjecture)
• Das Collatz-Problem von Jürgen Dankert – Interaktives Skript zum (3n+1)- und (3n−1)-Problem zum Erzeugen von Folgen mit beliebig großen Startzahlen
• Terence Tao: The Collatz conjecture, Littlewood-Offord theory, and powers of 2 and 3, 25. August 2011
• Paul J. Andaloro: The 3x+1 problem and directed graphs (PDF; 3,8 MB), Fibonacci Quarterly 40, 2002 (englisch)
• The Simplest Math Problem No One Can Solve – Veritasium auf YouTube (englisch)