Teoria Delle Categorie

La nozione di categoria fu introdotta per la prima volta da Samuel Eilenberg e Saunders Mac Lane nel 1945 nell'ambito della topologia algebrica. Le categorie ora appaiono in molte discipline della matematica e in alcune aree dell'informatica teorica e della fisica matematica costituendo una nozione unificante. Informalmente, una categoria è costituita da determinate strutture matematiche e dalle mappe tra esse che ne conservano le operazioni.

Definizione

Una categoria ${\displaystyle {\mathcal {C}}}$  consiste di quanto segue.

• Una classe ${\displaystyle {\text{ob}}({\mathcal {C}})}$  i cui elementi sono chiamati oggetti.
• Una classe ${\displaystyle {\text{mor}}({\mathcal {C}})}$  i cui elementi sono chiamati morfismi, mappe o frecce. Ogni morfismo ha associati un unico oggetto sorgente ${\displaystyle a}$  e un unico oggetto destinazione ${\displaystyle b}$  in ${\displaystyle {\text{ob}}({\mathcal {C}})}$ . La scrittura ${\displaystyle f:a\to b}$  indica che ${\displaystyle f}$  è un morfismo con sorgente ${\displaystyle a}$  e destinazione ${\displaystyle b}$ . L'insieme dei morfismi da ${\displaystyle a}$  a ${\displaystyle b}$  è indicato con ${\displaystyle {\text{mor}}(a,b)}$ .
• Per ogni terna di oggetti ${\displaystyle a}$ , ${\displaystyle b}$  e ${\displaystyle c}$  di ${\displaystyle {\mathcal {C}}}$ , è definita una funzione ${\displaystyle {\text{mor}}(b,c)\times {\text{mor}}(a,b)\to {\text{mor}}(a,c)}$ , chiamata composizione di morfismi. La composizione di ${\displaystyle f:b\to c}$  con ${\displaystyle g:a\to b}$  si indica con ${\displaystyle f\circ g:a\to c}$  (talvolta si indica semplicemente ${\displaystyle fg}$ ).

La composizione deve soddisfare i seguenti assiomi:

• (associatività) se ${\displaystyle f:a\to b}$ , ${\displaystyle g:b\to c}$  e ${\displaystyle h:c\to d}$ , allora ${\displaystyle h\circ (g\circ f)=(h\circ g)\circ f}$ 
• (identità) per ogni oggetto ${\displaystyle x}$  esiste un morfismo ${\displaystyle {\text{id}}_{x}:x\to x}$ , chiamato morfismo identità su ${\displaystyle x}$ , tale che per ogni morfismo ${\displaystyle f:a\to x}$  vale ${\displaystyle {\text{id}}_{x}\circ f=f}$  e per ogni morfismo ${\displaystyle g:x\to b}$  si ha ${\displaystyle g\circ {\text{id}}_{x}=g}$ .

Dagli assiomi si deduce che ad ogni oggetto è associato un unico morfismo identità. Questo permette di dare una definizione diversa di categoria, data dalla sola classe dei morfismi: gli oggetti vengono identificati a posteriori con i corrispondenti morfismi identità.

Una categoria si dice piccola se la classe degli oggetti è un insieme e grande se è una classe propria. Molte importanti categorie sono grandi.

Esempi

Negli esempi le categorie sono indicate tramite i loro oggetti e i corrispondenti morfismi.

• Gli insiemi e le funzioni tra essi
• I monoidi e gli omomorfismi tra essi
• I gruppi coi loro omomorfismi
• Gli spazi vettoriali e le funzioni lineari
• Gli spazi topologici e le funzioni continue
• Gli spazi misurabili e le funzioni misurabili
• Le varietà differenziabili e le funzioni differenziabili

• Ogni monoide forma una categoria piccola con un singolo oggetto ${\displaystyle X}$  (il monoide stesso) avendo come morfismi le traslazioni associate agli elementi del monoide. (L'azione di un elemento di X su un qualunque altro elemento è definita dall'operazione binaria del monoide).
• Se I è un insieme, la categoria discreta su I è la categoria piccola che ha come oggetti gli elementi di I e come morfismi solo i morfismi identità.
• Da ogni categoria C si può definire una nuova categoria, la categoria duale ${\displaystyle C^{*}}$  che ha per oggetti gli stessi oggetti di C, ma che inverte la direzione dei morfismi (l'insieme ${\displaystyle Mor(A,B)}$  diventa l'insieme ${\displaystyle Mor(B,A)}$ ).
• Se (C,o') e (D,o") sono categorie, si può definire la categoria prodotto, i cui oggetti sono coppie (c,d) aventi per primo elemento un oggetto di C e per secondo un oggetto di D, i morfismi sono analoghe coppie di morfismi; la composizione viene definita componente per componente: ${\displaystyle (c_{1},d_{1})\circ (c_{2},d_{2}):=(c_{1}\circ 'c_{2}\,,\,d_{1}\circ ''d_{2})}$ .

Sebbene esistano dei "morfismi" tra le categorie (i funtori) non è possibile definire la "categoria delle categorie", in quanto le categorie che sono classi proprie non possono appartenere ad altre classi (per definizione). È possibile invece parlare della categoria delle categorie piccole, le quali, essendo insiemi, possono appartenere a una classe e quindi essere oggetti di una categoria.

Tipi di morfismi

Un morfismo f: A → B si chiama

• monomorfismo se ${\displaystyle fg_{1}=fg_{2}\Rightarrow g_{1}=g_{2}}$  per tutti i morfismi ${\displaystyle g_{1},g_{2}:X\rightarrow A}$ .
• epimorfismo se g₁f = g₂f implica g₁ = g₂ per tutti i morfismi g₁, g₂ : B → X.
• isomorfismo se esiste un morfismo g : B → A con fg = id_B e gf = id_A.
• endomorfismo se A = B.
• automorfismo se f è insieme un endomorfismo e un isomorfismo.

  Lo stesso argomento in dettaglio: Funtore (matematica).

I funtori sono mappe tra le categorie che ne conservano le strutture.

Un funtore covariante dalla categoria C alla categoria D è una mappa che associa:

• ad ogni oggetto X in C un oggetto F(X) in D
• ad ogni morfismo f:X→Y un morfismo F(f):F(X)→F(Y)

in modo tale che valgano le seguenti proprietà:

• F(id_X) = id_F(X) per ogni oggetto X in C.
• F(g ${\displaystyle \circ }$  f) = F(g) ${\displaystyle \circ }$  F(f) per tutti i morfismi f : X → Y e g : Y → Z.

Un funtore contravariante è definito in maniera analoga, ma inverte i morfismi, cioè se f:X→ Y, allora F(f):F(Y)→ F(X). Dato un funtore covariante da C a D, il corrispondente funtore da C^* a D è contravariante.

Due funtori F, G : C → D ci danno due rappresentazioni di C in D. Una trasformazione naturale è una associazione che permette di "tradurre" l'immagine che ne dà F in quella che ne dà G.

Se F e G sono funtori (covarianti) tra le categorie C e D, allora una trasformazione naturale da F a G associa a ogni oggetto X di C un morfismo η_X : F(X) → G(X) in D tale che per ogni morfismo f : X → Y in C abbiamo η_Y ${\displaystyle _{\circ }}$  F(f) = G(f) ${\displaystyle _{\circ }}$  η_X; vale a dire che η rende commutativo il diagramma

 

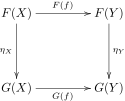
I due funtori F e G si dicono naturalmente isomorfi se esiste una trasformazione naturale da F a G tale che η_X sia un isomorfismo tra oggetti in D per ogni oggetto X in C.

• (EN) Jiří Adámek, Horst Herrlich, George E. Strecker (1990): Abstract and Concrete Categories Archiviato il 21 aprile 2015 in Internet Archive., John Wiley & Sons ISBN 0-471-60922-6
• (EN) Francis Borceux (1994): Handbook of Categorical Algebra I. Basic Category Theory, Cambridge University Press, ISBN 0-521-44178-1
• (EN) Francis Borceux (1994): Handbook of Categorical Algebra II. Categories and Structures, Cambridge University Press, ISBN 0-521-44179-X
• (EN) Francis Borceux (1994): Handbook of Categorical Algebra III. Categories of Sheaves, Cambridge University Press, ISBN 0-521-44180-3
• (EN) Robert Goldblatt (1984): Topoi: The Categorial Analysis of Logic, Dover
• William Lawvere, Steve Schanuel (1994): Teoria delle categorie: un'introduzione alla matematica, Franco Muzzio
• (EN) William Lawvere, Steve Schanuel (1997): Conceptual Mathematics: A First Introduction to Categories, Cambridge University Press
• (EN) Saunders Mac Lane (1998): Categories for the Working Mathematician (seconda edizione), Springer ISBN 0-387-98403-8
• (EN) Michael Barr, Charles Wells (2002): Toposes, Triples and Theories

• Progetto:Matematica/Elenco di voci sulla teoria delle categorie
• Funtore (matematica)
• Diagramma commutativo
• Gruppoide (teoria delle categorie)
• Categoria monoidale
• Categoria abeliana
• Lemma di Yoneda

•   Wiki Commons contiene immagini o altri file sulla teoria delle categorie

• Santuzza Baldassarri Ghezzo, CATEGORIE, Teoria delle, in Enciclopedia Italiana, IV Appendice, Istituto dell'Enciclopedia Italiana, 1978.  
• (EN) category theory, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.  
• (EN) Jean-Pierre Marquis, Category Theory, su Stanford Encyclopedia of Philosophy.  
• (EN) Eric W. Weisstein, Category Theory, su MathWorld, Wolfram Research.  
• Note sulla teoria delle categorie^{[collegamento interrotto]} (in inglese, file .ps compresso con Gzip)

  Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica