Algorithme D'euclide: Algorithme d'arithmétique calculant le PGCD de deux entiers

L'algorithme ne requiert pas de connaître la factorisation de ces deux nombres.

 

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

 

Selon Donald Knuth, l'algorithme d'Euclide est l'un des plus anciens algorithmes. Il est décrit dans le livre VII (Proposition 1-3) des Éléments d'Euclide (vers 300 av. J.-C.) sous la forme de l'anthyphérèse. Il est aussi décrit dans le livre X (Proposition 2), mais pour un problème de façon géométrique : comment trouver une « unité de mesure » commune pour deux longueurs de segments. Il procède par soustractions répétées de la longueur du plus court segment sur la longueur du plus long. Cela correspond à une adaptation de la méthode naïve de calcul de la division euclidienne, telle que décrite dans l'article consacré. Pour ce problème géométrique, l'algorithme d'Euclide ne termine pas forcément (dans un langage plus moderne, cela correspond à exécuter l'algorithme d'Euclide pour des nombres réels).

L'algorithme n'a probablement pas été découvert par Euclide, qui aurait compilé des résultats d'autres mathématiciens dans ses Éléments^,. Pour le mathématicien et historien B. L. van der Waerden, le livre VII vient d'un livre de théorie des nombres écrit par un mathématicien de l'école de Pythagore. L'algorithme était probablement connu d'Eudoxe de Cnide (vers 375 av. J.-C.)^,. Il se peut même que l'algorithme ait existé avant Eudoxe^,, vu les termes techniques ἀνθυφαίρεσις (anthyphairesis, soustraction réciproque) dans les travaux d'Euclide et aussi d'Aristote.

Quelques siècles plus tard, l'algorithme d'Euclide est inventé de manière indépendante à la fois en Inde et en Chine. L'objectif était de résoudre des équations diophantiennes issues de l'astronomie et de faire des calendriers plus précis. Au V^e siècle, le mathématicien et astronome indien Aryabhata a décrit cet algorithme comme le « pulvérisateur », à cause de son efficacité pour résoudre les équations diophantiennes.

Principe

Le PGCD (plus grand commun diviseur) de deux entiers relatifs est égal au PGCD de leurs valeurs absolues : de ce fait, on se restreint dans cette section aux entiers positifs. L'algorithme part du constat suivant : le PGCD de deux nombres n'est pas changé si on remplace le plus grand d'entre eux par leur différence. Autrement dit, pgcd(a, b) = pgcd(a−b, b). Par exemple, le PGCD de 252 et 105 vaut 21, mais c'est aussi le PGCD de 252 − 105 = 147 et 105. Ainsi, comme le remplacement de ces nombres diminue strictement le plus grand d'entre eux, on peut continuer le processus, jusqu'à obtenir deux nombres égaux.

Dans l'algorithme, on pourrait réaliser autant de différences que l'on souhaite.^[pas clair] Par exemple, le PGCD de 252 et 105 est aussi égal au PGCD de 105 et 252 − 2 × 105 = 42. Ainsi, l'algorithme d'Euclide opère ainsi : on remplace le plus grand des deux nombres par le reste de la division euclidienne du plus grand nombre par le plus petit. Par exemple, la division euclidienne de 252 par 105 donne un reste de 42. Dans Introduction à l'algorithmique de Cormen et al. (voir Th. 31.9), les auteurs appellent théorème de la récursivité pour le PGCD le fait suivant :

pgcd(a, b) = pgcd(b, r) où r est le reste de la division euclidienne de a par b.

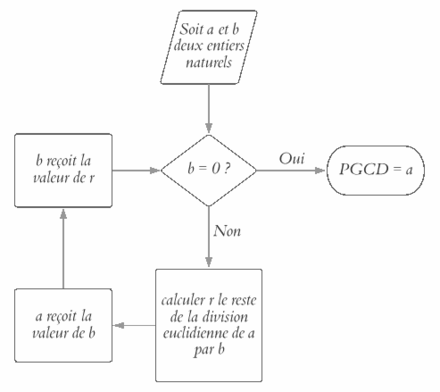
Ainsi, l'algorithme d'Euclide sur deux nombres entiers positifs a et b avec a > b ⩾ 0 procède comme suit :

• si b = 0, l'algorithme termine et rend la valeur a ;
• sinon, l'algorithme calcule le reste r de la division euclidienne de a par b, puis recommence avec a := b et b := r.

Formellement l'algorithme d'Euclide construit une suite finie d'entiers (r_n) par récurrence double :

• r₀ = a, r₁ = b ;
• pour n ⩾ 1, r_n+1 est le reste de la division euclidienne de r_n-1 par r_n, en particulier r_n+1 < r_n.

La suite (r_n) est une suite strictement décroissante d'entiers positifs à partir du rang 1 : elle est donc finie et s'arrête au premier n tel que r_n = 0.

Exemple

Le tableau suivant montre le calcul du PGCD de 21 et 15. On réalise la division euclidienne de a = 21 et b = 15 : le quotient est 1 et le reste 6. L'algorithme continue avec a := b et b := le précédent reste, jusqu'à trouver un reste nul. L'algorithme s'arrête alors et retourne le dernier reste non nul trouvé, ici ${\displaystyle r_{3}=3}$  qui est bien le PGCD de 21 et 15 :

Étape n	Dividende ${\displaystyle r_{n-1}}$	Diviseur ${\displaystyle r_{n}}$	Équation ${\displaystyle r_{n-1}=r_{n}q_{n}+r_{n+1}}$	Quotient ${\displaystyle q_{n}}$	Reste ${\displaystyle r_{n+1}}$
1	21	15	21 = 15 × 1 + 6	1	6
2	15	6	15 = 6 × 2 + 3	2	3
3	6	3	6 = 3 × 2 + 0	2	0
4	3	0	fin de l'algorithme

Explications géométriques

Dans la tradition grecque, en comprenant un nombre entier comme une longueur et un couple d'entiers comme un rectangle, leur PGCD est la longueur du côté du plus grand carré permettant de carreler entièrement ce rectangle. L'algorithme décompose ce rectangle en carrés, de plus en plus petits, par divisions euclidiennes successives, de la longueur par la largeur, puis de la largeur par le reste, jusqu'à un reste nul.

Considérons par exemple le rectangle de dimensions L = 21 par l = 15 représenté ci-dessous. On peut glisser un carré de côté 15 mais il reste un rectangle de côtés 15 et 6. On peut y glisser deux carrés de côté 6 mais il reste un rectangle de côtés 6 et 3 que l'on peut carreler entièrement de carrés de côté 3. Les carrés de côté 6 ou 15 peuvent aussi se carreler en carrés de côté 3. Le rectangle entier peut se carreler en carrés de côté 3. Il n'existe pas de carré plus grand permettant un tel carrelage.

 

Version itérative

 

Donald Knuth, dans The Art of Computer Programming, écrit une version itérative de l'algorithme d'Euclide :

‎

où l'on note a modulo b le reste de la division euclidienne de a et b.

La version originale de l'algorithme d'Euclide, où l'on n’effectue que des différences successives, est :

‎

Version récursive

Cormen et al., dans Introduction à l'algorithmique en donne une version récursive ; Dasgupta et al. en donne la même version :

‎

L'appel à euclide(a, b) s'arrête et retourne la valeur a si b = 0. Sinon, l'appel continue avec les nombres b et a modulo b. L'exécution du calcul de PGCD de 21 et 15 donne : euclide(21, 15) = euclide(15, 6) = euclide(6, 3) = euclide(3, 0) = 3.

Correction et terminaison

On sait que PGCD(a, 0) = a et que PGCD(a, b) = PGCD(b, a mod b). On progresse dans l'algorithme en diminuant à chaque étape les nombres considérés par calcul du modulo. L'algorithme termine bien : pour une valeur non nulle de b, le calcul de PGCD(a, b) fait appel au calcul de PGCD(a’, b’), où 0 ≤ b’ < |b|, car b’ est le reste d'une division euclidienne par b.

 

Dans cette section, nous étudions la complexité temporelle de l'algorithme d'Euclide, c'est-à-dire le nombre d'étapes de calcul en fonction des entiers a et b. La première analyse de complexité connue est due à A. L. Reynaud en 1811 : il écrit que le nombre d'étapes de l'algorithme d'Euclide sur a et b est borné par b^,. En 1841, P.-J.-E. Finck démontre que le nombre d'étapes est borné par 2 log₂ b + 1. Cela démontre que l'algorithme d'Euclide s'exécute en temps polynomial en la taille de l'entrée (nombre de chiffres pour écrire les nombres a et b). En 1844, Gabriel Lamé raffine les résultats de Finck : il démontre que l'algorithme effectue au plus 5 fois le nombre de chiffres en base 10 du plus petit nombre.

Première analyse

Nous donnons d'abord une analyse qui part du constat suivant :

Si a ≥ b, alors a mod b < a / 2

Ainsi, si a et b sont codés sur n bits, au bout de deux appels récursifs, leurs tailles contient un bit de moins. Il y a donc O(n) appels récursifs. Comme la division euclidienne s'exécute en O(n²) opérations, l'algorithme d'Euclide est en O(n³).

Analyse via le théorème de Lamé

La précédente analyse permet de montrer rapidement que l'algorithme d'Euclide est en O(log₂(b)) divisions. Une analyse plus fine, due pour l'essentiel à Lamé, permet une meilleure évaluation (c'est la constante pour cette évaluation en O(log₂(b)) qui peut être améliorée). Elle utilise la suite de Fibonacci définie par

F₀ = 0, F₁ = 1, F_k+2 = F_k+1 + F_k, pour tout k ≥ 0,

et dont les premiers termes sont :

${\displaystyle F_{0}}$	${\displaystyle F_{1}}$	${\displaystyle F_{2}}$	${\displaystyle F_{3}}$	${\displaystyle F_{4}}$	${\displaystyle F_{5}}$	${\displaystyle F_{6}}$	${\displaystyle F_{7}}$	${\displaystyle F_{8}}$	${\displaystyle F_{9}}$	${\displaystyle F_{10}}$	${\displaystyle F_{11}}$	${\displaystyle F_{12}}$	${\displaystyle F_{13}}$	${\displaystyle F_{14}}$	${\displaystyle F_{15}}$	${\displaystyle F_{16}}$	...
0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	...

.

Quand l'algorithme d'Euclide est appelé sur deux nombres de Fibonacci consécutifs F_k+2 et F_k+1 , il utilise k appels récursifs :

euclide( F_k+2 , F_k+1 ) = euclide( F_k+1 , F_k ) = ... euclide(F₂, F₁) = euclide(F₁, F₀)

et comme pour chaque division euclidienne invoquée par l'algorithme le quotient est 1, cette situation est la pire du point de vue de la complexité, plus précisément on a le théorème de Lamé :

Cette majoration est la meilleure possible, puisqu'elle est atteinte quand ${\displaystyle a}$  et ${\displaystyle b}$  sont deux nombres de Fibonacci consécutifs.

Via la formule de Binet, F_k est équivalent à ${\displaystyle \varphi ^{k}/{\sqrt {5}}}$  où ${\displaystyle \varphi }$  est le nombre d'or. Ainsi, on en déduit à nouveau que le nombre d'appels récursifs est ${\displaystyle O(\log(b))}$ . Plus précisément, il y a au plus ${\displaystyle 1+\log _{\varphi }(b)}$  appels récursifs, où ${\displaystyle \log _{\varphi }}$ désigne le logarithme en base ${\displaystyle \varphi }$ . On peut même montrer qu'il y a ${\displaystyle 1+\log _{\varphi }(b/pgcd(a,b))}$ .

Complexité quadratique

Soit n le nombre de bits dans les nombres d'entrées. Comme l'algorithme effectue une division euclidienne à chaque appel récursif, qui coûte O(n²), et qu'il y a O(n) appels récursifs, l'algorithme est en O(n³). Toutefois, une analyse fine montre que l'algorithme s'exécute en temps quadratique en le nombre de bits des nombres d'entrées (voir Problème 31.2 laissé en exercice dans , p. 902).

Anneau euclidien

Cet algorithme repose sur la structure d’anneau euclidien de l’anneau Z des entiers relatifs, plus particulièrement sur la propriété de division euclidienne. Il se généralise donc à d’autres anneaux, en particulier les anneaux de polynômes à coefficients dans un corps. L’algorithme se généralise pour permettre le calcul des coefficients de Bézout.

L’algorithme est effectif à condition de disposer d’un algorithme effectif de division euclidienne. La possibilité de disposer d’un tel algorithme rend de nombreux autres calculs effectifs, notamment, en algèbre linéaire, le calcul de facteurs invariants.

Algorithme étendu aux coefficients de Bézout

Le théorème de Bachet-Bézout assure l'existence de deux entiers u et v tels que : ${\displaystyle au+bv=PGCD(a,b)}$ . L'algorithme d'Euclide étendu calcule de tels coefficients.

Pour cela, on introduit deux suites ${\displaystyle (u_{n})}$  et ${\displaystyle (v_{n})}$  telles que pour tout n, on ait la relation : ${\displaystyle au_{n}+bv_{n}=a_{n}}$ où ${\displaystyle a_{n}}$ est la valeur de ${\displaystyle a}$  à la nème étape de l'algorithme. Les termes ${\displaystyle u_{N},v_{N}}$  constitueront une paire de coefficients de Bézout pour a et b, où N est le numéro de la dernière étape de l'algorithme.

On choisit ${\displaystyle u_{0}=1,v_{0}=0}$  et ${\displaystyle u_{1}=0,v_{1}=1}$  (afin que ${\displaystyle au_{n}+bv_{n}=a_{n}}$  soit vrai pour n = 0 et pour n = 1), puis la relation de récurrence de pas 2 entre les ${\displaystyle a_{n}}$  montre :

${\displaystyle a_{n+2}=a_{n}-q_{n+2}a_{n+1}=au_{n}+bv_{n}-q_{n+2}(au_{n+1}+bv_{n+1})=a(u_{n}-q_{n+2}u_{n+1})+b(v_{n}-q_{n+2}v_{n+1})}$ 

On peut ainsi définir ${\displaystyle (u_{n})}$  par la relation de récurrence de pas 2 : ${\displaystyle u_{n+2}=u_{n}-q_{n+2}u_{n+1}}$  et l'initialisation précédente, et ${\displaystyle (v_{n})}$  par ${\displaystyle v_{n+2}=v_{n}-q_{n+2}v_{n+1}}$  et l'initialisation précédente ; et on obtient bien la relation annoncée pour tout n.

L'algorithme étendu s'implémente comme l'algorithme classique ; il suffit de rajouter des variables correspondant aux coefficients u et v à calculer, et de faire une multiplication et une soustraction supplémentaires, pour calculer chacun des deux nouveaux coefficients, à chaque étape.

Fractions continues

Les quotients successifs qui apparaissent quand l'algorithme d'Euclide est appliqué aux données a et b, sont précisément les nombres qui apparaissent dans la représentation sous forme de fraction continue de a/b. Considérons l'exemple de a = 1 071 et b = 1 029 utilisé ci-dessus.

Voici le calcul avec les quotients soulignés (successivement 1, 24 et 2) :

1 071 = 1 029 × 1 + 42
1 029 = 42 × 24 + 21
42 = 21 × 2 + 0

De cela on tire :

${\displaystyle {\frac {1071}{1029}}=\mathbf {1} +{\frac {1}{\mathbf {24} +{\frac {1}{\mathbf {2} }}}}}$ .

Dans l'égalité précédente, le second membre s'appelle la fraction continue ou continuée du quotient 1 071/1 029.

On peut en déduire les trois approximations suivantes de la fraction, classées par ordre de précision croissante :

• ${\displaystyle {\frac {1071}{1029}}\simeq \mathbf {1} ={\frac {1}{1}}}$  ;
• ${\displaystyle {\frac {1071}{1029}}\simeq \mathbf {1} +{\frac {1}{\mathbf {24} }}={\frac {25}{24}}}$  ;
• ${\displaystyle {\frac {1071}{1029}}=\mathbf {1} +{\frac {1}{\mathbf {24} +{\frac {1}{\mathbf {2} }}}}={\frac {51}{49}}}$ .

Cette méthode peut également être utilisée pour des nombres réels a et b ; comme dans le cas de deux entiers, la suite de quotients calculés représente la « décomposition en fraction continue » de a/b et fournit une suite d'approximations successives, de qualité croissante, du quotient a/b. Dans le cas où ce quotient est irrationnel, l'algorithme d'Euclide ne termine pas et la suite des approximations obtenues est infinie^{[réf. nécessaire]}.

Nota : La décomposition en fraction continue (et la série d'approximations successives correspondante) peut être appliquée, non seulement à un nombre réel quelconque, mais également à une fonction : cette démarche consiste à rechercher les approximants de Padé, dont on peut définir le principe comme suit : Au voisinage d'un point, le développement en série de Taylor d'une fonction donnée fournit un polynôme qui réalise une approximation de la fonction. Mais on peut également chercher une fraction rationnelle qui satisfasse les mêmes conditions que la partie polynomiale du développement de Taylor : l'égalité des dérivées de la fonction et de son approximation, jusqu'à un certain ordre donné^{[réf. nécessaire]}.

La comparaison de ces deux types de développements permet de très intéressants développements, comme la démonstration de l'irrationalité de ζ(3)^{[réf. nécessaire]}