Lebesgue Measure
In measure theory, a branch of mathematics, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of higher dimensional Euclidean n-spaces.
For lower dimensions n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called n-dimensional volume, n-volume, hypervolume, or simply volume. It is used throughout real analysis, in particular to define Lebesgue integration. Sets that can be assigned a Lebesgue measure are called Lebesgue-measurable; the measure of the Lebesgue-measurable set A is here denoted by λ(A).
Henri Lebesgue described this measure in the year 1901 which, a year after, was followed up by his description of the Lebesgue integral. Both were published as part of his dissertation in 1902.
Definition
For any interval 





The above definition can be generalised to higher dimensions as follows. For any rectangular cuboid 



Some sets 

The sets 


A set 
Intuition
The first part of the definition states that the subset 







That characterizes the Lebesgue outer measure. Whether this outer measure translates to the Lebesgue measure proper depends on an additional condition. This condition is tested by taking subsets 
















Examples
- Any closed interval [a, b] of real numbers is Lebesgue-measurable, and its Lebesgue measure is the length b − a. The open interval (a, b) has the same measure, since the difference between the two sets consists only of the end points a and b, which each have measure zero.
- Any Cartesian product of intervals [a, b] and [c, d] is Lebesgue-measurable, and its Lebesgue measure is (b − a)(d − c), the area of the corresponding rectangle.
- Moreover, every Borel set is Lebesgue-measurable. However, there are Lebesgue-measurable sets which are not Borel sets.
- Any countable set of real numbers has Lebesgue measure 0. In particular, the Lebesgue measure of the set of algebraic numbers is 0, even though the set is dense in
.
- The Cantor set and the set of Liouville numbers are examples of uncountable sets that have Lebesgue measure 0.
- If the axiom of determinacy holds then all sets of reals are Lebesgue-measurable. Determinacy is however not compatible with the axiom of choice.
- Vitali sets are examples of sets that are not measurable with respect to the Lebesgue measure. Their existence relies on the axiom of choice.
- Osgood curves are simple plane curves with positive Lebesgue measure (it can be obtained by small variation of the Peano curve construction). The dragon curve is another unusual example.
- Any line in
, for
, has a zero Lebesgue measure. In general, every proper hyperplane has a zero Lebesgue measure in its ambient space.
- The volume of an n-ball can be calculated in terms of Euler's gamma function.
Properties
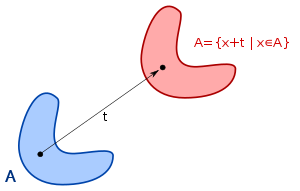
 and
and  are the same.
are the same.The Lebesgue measure on Rn has the following properties:
- If A is a cartesian product of intervals I1 × I2 × ⋯ × In, then A is Lebesgue-measurable and
- If A is a disjoint union of countably many disjoint Lebesgue-measurable sets, then A is itself Lebesgue-measurable and λ(A) is equal to the sum (or infinite series) of the measures of the involved measurable sets.
- If A is Lebesgue-measurable, then so is its complement.
- λ(A) ≥ 0 for every Lebesgue-measurable set A.
- If A and B are Lebesgue-measurable and A is a subset of B, then λ(A) ≤ λ(B). (A consequence of 2.)
- Countable unions and intersections of Lebesgue-measurable sets are Lebesgue-measurable. (Not a consequence of 2 and 3, because a family of sets that is closed under complements and disjoint countable unions does not need to be closed under countable unions:
.)
- If A is an open or closed subset of Rn (or even Borel set, see metric space), then A is Lebesgue-measurable.
- If A is a Lebesgue-measurable set, then it is "approximately open" and "approximately closed" in the sense of Lebesgue measure.
- A Lebesgue-measurable set can be "squeezed" between a containing open set and a contained closed set. This property has been used as an alternative definition of Lebesgue measurability. More precisely,
is Lebesgue-measurable if and only if for every
there exist an open set
and a closed set
such that
and
.
- A Lebesgue-measurable set can be "squeezed" between a containing Gδ set and a contained Fσ. I.e, if A is Lebesgue-measurable then there exist a Gδ set G and an Fσ F such that G ⊇ A ⊇ F and λ(G \ A) = λ(A \ F) = 0.
- Lebesgue measure is both locally finite and inner regular, and so it is a Radon measure.
- Lebesgue measure is strictly positive on non-empty open sets, and so its support is the whole of Rn.
- If A is a Lebesgue-measurable set with λ(A) = 0 (a null set), then every subset of A is also a null set. A fortiori, every subset of A is measurable.
- If A is Lebesgue-measurable and x is an element of Rn, then the translation of A by x, defined by A + x = {a + x : a ∈ A}, is also Lebesgue-measurable and has the same measure as A.
- If A is Lebesgue-measurable and
, then the dilation of
by
defined by
is also Lebesgue-measurable and has measure
- More generally, if T is a linear transformation and A is a measurable subset of Rn, then T(A) is also Lebesgue-measurable and has the measure
.
All the above may be succinctly summarized as follows (although the last two assertions are non-trivially linked to the following):
- The Lebesgue-measurable sets form a σ-algebra containing all products of intervals, and λ is the unique complete translation-invariant measure on that σ-algebra with
The Lebesgue measure also has the property of being σ-finite.
Null sets
A subset of Rn is a null set if, for every ε > 0, it can be covered with countably many products of n intervals whose total volume is at most ε. All countable sets are null sets.
If a subset of Rn has Hausdorff dimension less than n then it is a null set with respect to n-dimensional Lebesgue measure. Here Hausdorff dimension is relative to the Euclidean metric on Rn (or any metric Lipschitz equivalent to it). On the other hand, a set may have topological dimension less than n and have positive n-dimensional Lebesgue measure. An example of this is the Smith–Volterra–Cantor set which has topological dimension 0 yet has positive 1-dimensional Lebesgue measure.
In order to show that a given set A is Lebesgue-measurable, one usually tries to find a "nicer" set B which differs from A only by a null set (in the sense that the symmetric difference (A − B) ∪ (B − A) is a null set) and then show that B can be generated using countable unions and intersections from open or closed sets.
Construction of the Lebesgue measure
The modern construction of the Lebesgue measure is an application of Carathéodory's extension theorem. It proceeds as follows.
Fix n ∈ N. A box in Rn is a set of the form
where bi ≥ ai, and the product symbol here represents a Cartesian product. The volume of this box is defined to be
For any subset A of Rn, we can define its outer measure λ*(A) by:
We then define the set A to be Lebesgue-measurable if for every subset S of Rn,
These Lebesgue-measurable sets form a σ-algebra, and the Lebesgue measure is defined by λ(A) = λ*(A) for any Lebesgue-measurable set A.
The existence of sets that are not Lebesgue-measurable is a consequence of the set-theoretical axiom of choice, which is independent from many of the conventional systems of axioms for set theory. The Vitali theorem, which follows from the axiom, states that there exist subsets of R that are not Lebesgue-measurable. Assuming the axiom of choice, non-measurable sets with many surprising properties have been demonstrated, such as those of the Banach–Tarski paradox.
In 1970, Robert M. Solovay showed that the existence of sets that are not Lebesgue-measurable is not provable within the framework of Zermelo–Fraenkel set theory in the absence of the axiom of choice (see Solovay's model).
Relation to other measures
The Borel measure agrees with the Lebesgue measure on those sets for which it is defined; however, there are many more Lebesgue-measurable sets than there are Borel measurable sets. The Borel measure is translation-invariant, but not complete.
The Haar measure can be defined on any locally compact group and is a generalization of the Lebesgue measure (Rn with addition is a locally compact group).
The Hausdorff measure is a generalization of the Lebesgue measure that is useful for measuring the subsets of Rn of lower dimensions than n, like submanifolds, for example, surfaces or curves in R3 and fractal sets. The Hausdorff measure is not to be confused with the notion of Hausdorff dimension.
It can be shown that there is no infinite-dimensional analogue of Lebesgue measure.
See also
References
This article uses material from the Wikipedia English article Lebesgue measure, which is released under the Creative Commons Attribution-ShareAlike 3.0 license ("CC BY-SA 3.0"); additional terms may apply (view authors). Content is available under CC BY-SA 4.0 unless otherwise noted. Images, videos and audio are available under their respective licenses.
®Wikipedia is a registered trademark of the Wiki Foundation, Inc. Wiki English (DUHOCTRUNGQUOC.VN) is an independent company and has no affiliation with Wiki Foundation.









