Fermat Number

The first few Fermat numbers are: 3, 5, 17, 257, 65537, 4294967297, 18446744073709551617, ... (sequence A000215 in the OEIS).

If 2^k + 1 is prime and k > 0, then k itself must be a power of 2, so 2^k + 1 is a Fermat number; such primes are called Fermat primes. As of 2023^[update], the only known Fermat primes are F₀ = 3, F₁ = 5, F₂ = 17, F₃ = 257, and F₄ = 65537 (sequence A019434 in the OEIS).

The Fermat numbers satisfy the following recurrence relations:

${\displaystyle F_{n}=(F_{n-1}-1)^{2}+1}$ 

${\displaystyle F_{n}=F_{0}\cdots F_{n-1}+2}$ 

for n ≥ 1,

${\displaystyle F_{n}=F_{n-1}+2^{2^{n-1}}F_{0}\cdots F_{n-2}}$ 

${\displaystyle F_{n}=F_{n-1}^{2}-2(F_{n-2}-1)^{2}}$ 

for n ≥ 2. Each of these relations can be proved by mathematical induction. From the second equation, we can deduce Goldbach's theorem (named after Christian Goldbach): no two Fermat numbers share a common integer factor greater than 1. To see this, suppose that 0 ≤ i < j and F_i and F_j have a common factor a > 1. Then a divides both

${\displaystyle F_{0}\cdots F_{j-1}}$ 

and F_j; hence a divides their difference, 2. Since a > 1, this forces a = 2. This is a contradiction, because each Fermat number is clearly odd. As a corollary, we obtain another proof of the infinitude of the prime numbers: for each F_n, choose a prime factor p_n; then the sequence {p_n} is an infinite sequence of distinct primes.

Further properties

• No Fermat prime can be expressed as the difference of two pth powers, where p is an odd prime.
• With the exception of F₀ and F₁, the last digit of a Fermat number is 7.
• The sum of the reciprocals of all the Fermat numbers (sequence A051158 in the OEIS) is irrational. (Solomon W. Golomb, 1963)

Fermat numbers and Fermat primes were first studied by Pierre de Fermat, who conjectured that all Fermat numbers are prime. Indeed, the first five Fermat numbers F₀, ..., F₄ are easily shown to be prime. Fermat's conjecture was refuted by Leonhard Euler in 1732 when he showed that

${\displaystyle F_{5}=2^{2^{5}}+1=2^{32}+1=4294967297=641\times 6700417.}$ 

Euler proved that every factor of F_n must have the form k 2ⁿ⁺¹ + 1 (later improved to k 2ⁿ⁺² + 1 by Lucas) for n ≥ 2.

That 641 is a factor of F₅ can be deduced from the equalities 641 = 2⁷ × 5 + 1 and 641 = 2⁴ + 5⁴. It follows from the first equality that 2⁷ × 5 ≡ −1 (mod 641) and therefore (raising to the fourth power) that 2²⁸ × 5⁴ ≡ 1 (mod 641). On the other hand, the second equality implies that 5⁴ ≡ −2⁴ (mod 641). These congruences imply that 2³² ≡ −1 (mod 641).

Fermat was probably aware of the form of the factors later proved by Euler, so it seems curious that he failed to follow through on the straightforward calculation to find the factor. One common explanation is that Fermat made a computational mistake.

There are no other known Fermat primes F_n with n > 4, but little is known about Fermat numbers for large n. In fact, each of the following is an open problem:

• Is F_n composite for all n > 4?
• Are there infinitely many Fermat primes? (Eisenstein 1844)
• Are there infinitely many composite Fermat numbers?
• Does a Fermat number exist that is not square-free?

As of 2024^[update], it is known that F_n is composite for 5 ≤ n ≤ 32, although of these, complete factorizations of F_n are known only for 0 ≤ n ≤ 11, and there are no known prime factors for n = 20 and n = 24. The largest Fermat number known to be composite is F_18233954, and its prime factor 7 × 2^18233956 + 1 was discovered in October 2020.

Heuristic arguments

Heuristics suggest that F₄ is the last Fermat prime.

The prime number theorem implies that a random integer in a suitable interval around N is prime with probability 1 / ln N. If one uses the heuristic that a Fermat number is prime with the same probability as a random integer of its size, and that F₅, ..., F₃₂ are composite, then the expected number of Fermat primes beyond F₄ (or equivalently, beyond F₃₂) should be

${\displaystyle \sum _{n\geq 33}{\frac {1}{\ln F_{n}}}<{\frac {1}{\ln 2}}\sum _{n\geq 33}{\frac {1}{\log _{2}(2^{2^{n}})}}={\frac {1}{\ln 2}}2^{-32}<3.36\times 10^{-10}.}$ 

One may interpret this number as an upper bound for the probability that a Fermat prime beyond F₄ exists.

This argument is not a rigorous proof. For one thing, it assumes that Fermat numbers behave "randomly", but the factors of Fermat numbers have special properties. Boklan and Conway published a more precise analysis suggesting that the probability that there is another Fermat prime is less than one in a billion.

Anders Bjorn and Hans Riesel estimated the number of square factors of Fermat numbers from F₅ onward as

${\displaystyle \sum _{n\geq 5}\sum _{k\geq 1}{\frac {1}{k(k2^{n}+1)\ln(k2^{n})}}<{\frac {\pi ^{2}}{6\ln 2}}\sum _{n\geq 5}{\frac {1}{n2^{n}}}\approx 0.02576;}$ 

in other words, there are unlikely to be any non-squarefree Fermat numbers, and in general square factors of ${\displaystyle a^{2^{n}}+b^{2^{n}}}$  are very rare for large n.

Equivalent conditions

Let ${\displaystyle F_{n}=2^{2^{n}}+1}$  be the nth Fermat number. Pépin's test states that for n > 0,

${\displaystyle F_{n}}$  is prime if and only if ${\displaystyle 3^{(F_{n}-1)/2}\equiv -1{\pmod {F_{n}}}.}$ 

The expression ${\displaystyle 3^{(F_{n}-1)/2}}$  can be evaluated modulo ${\displaystyle F_{n}}$  by repeated squaring. This makes the test a fast polynomial-time algorithm. But Fermat numbers grow so rapidly that only a handful of them can be tested in a reasonable amount of time and space.

There are some tests for numbers of the form k 2^m + 1, such as factors of Fermat numbers, for primality.

Proth's theorem (1878). Let N = k 2^m + 1 with odd k < 2^m. If there is an integer a such that
${\displaystyle a^{(N-1)/2}\equiv -1{\pmod {N}}}$ 
then ${\displaystyle N}$  is prime. Conversely, if the above congruence does not hold, and in addition
${\displaystyle \left({\frac {a}{N}}\right)=-1}$  (See Jacobi symbol)
then ${\displaystyle N}$  is composite.

If N = F_n > 3, then the above Jacobi symbol is always equal to −1 for a = 3, and this special case of Proth's theorem is known as Pépin's test. Although Pépin's test and Proth's theorem have been implemented on computers to prove the compositeness of some Fermat numbers, neither test gives a specific nontrivial factor. In fact, no specific prime factors are known for n = 20 and 24.

Because of Fermat numbers' size, it is difficult to factorize or even to check primality. Pépin's test gives a necessary and sufficient condition for primality of Fermat numbers, and can be implemented by modern computers. The elliptic curve method is a fast method for finding small prime divisors of numbers. Distributed computing project Fermatsearch has found some factors of Fermat numbers. Yves Gallot's proth.exe has been used to find factors of large Fermat numbers. Édouard Lucas, improving Euler's above-mentioned result, proved in 1878 that every factor of the Fermat number ${\displaystyle F_{n}}$ , with n at least 2, is of the form ${\displaystyle k\times 2^{n+2}+1}$  (see Proth number), where k is a positive integer. By itself, this makes it easy to prove the primality of the known Fermat primes.

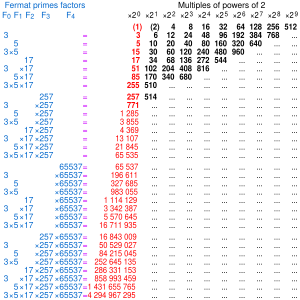
Factorizations of the first twelve Fermat numbers are:

F0	=	21	+	1	=	3 is prime
F1	=	22	+	1	=	5 is prime
F2	=	24	+	1	=	17 is prime
F3	=	28	+	1	=	257 is prime
F4	=	216	+	1	=	65,537 is the largest known Fermat prime
F5	=	232	+	1	=	4,294,967,297
					=	641 × 6,700,417 (fully factored 1732)
F6	=	264	+	1	=	18,446,744,073,709,551,617 (20 digits)
					=	274,177 × 67,280,421,310,721 (14 digits) (fully factored 1855)
F7	=	2128	+	1	=	340,282,366,920,938,463,463,374,607,431,768,211,457 (39 digits)
					=	59,649,589,127,497,217 (17 digits) × 5,704,689,200,685,129,054,721 (22 digits) (fully factored 1970)
F8	=	2256	+	1	=	115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,913,129, 639,937 (78 digits)
					=	1,238,926,361,552,897 (16 digits) × 93,461,639,715,357,977,769,163,558,199,606,896,584,051,237,541,638,188,580,280,321 (62 digits) (fully factored 1980)
F9	=	2512	+	1	=	13,407,807,929,942,597,099,574,024,998,205,846,127,479,365,820,592,393,377,723,561,443,721,764,0 30,073,546,976,801,874,298,166,903,427,690,031,858,186,486,050,853,753,882,811,946,569,946,433,6 49,006,084,097 (155 digits)
					=	2,424,833 × 7,455,602,825,647,884,208,337,395,736,200,454,918,783,366,342,657 (49 digits) × 741,640,062,627,530,801,524,787,141,901,937,474,059,940,781,097,519,023,905,821,316,144,415,759, 504,705,008,092,818,711,693,940,737 (99 digits) (fully factored 1990)
F10	=	21024	+	1	=	179,769,313,486,231,590,772,930...304,835,356,329,624,224,137,217 (309 digits)
					=	45,592,577 × 6,487,031,809 × 4,659,775,785,220,018,543,264,560,743,076,778,192,897 (40 digits) × 130,439,874,405,488,189,727,484...806,217,820,753,127,014,424,577 (252 digits) (fully factored 1995)
F11	=	22048	+	1	=	32,317,006,071,311,007,300,714,8...193,555,853,611,059,596,230,657 (617 digits)
					=	319,489 × 974,849 × 167,988,556,341,760,475,137 (21 digits) × 3,560,841,906,445,833,920,513 (22 digits) × 173,462,447,179,147,555,430,258...491,382,441,723,306,598,834,177 (564 digits) (fully factored 1988)

As of April 2023^[update], only F₀ to F₁₁ have been completely factored. The distributed computing project Fermat Search is searching for new factors of Fermat numbers. The set of all Fermat factors is A050922 (or, sorted, A023394) in OEIS.

The following factors of Fermat numbers were known before 1950 (since then, digital computers have helped find more factors):

Year	Finder	Fermat number	Factor
1732	Euler	${\displaystyle F_{5}}$	${\displaystyle 5\cdot 2^{7}+1}$
1732	Euler	${\displaystyle F_{5}}$  (fully factored)	${\displaystyle 52347\cdot 2^{7}+1}$
1855	Clausen	${\displaystyle F_{6}}$	${\displaystyle 1071\cdot 2^{8}+1}$
1855	Clausen	${\displaystyle F_{6}}$  (fully factored)	${\displaystyle 262814145745\cdot 2^{8}+1}$
1877	Pervushin	${\displaystyle F_{12}}$	${\displaystyle 7\cdot 2^{14}+1}$
1878	Pervushin	${\displaystyle F_{23}}$	${\displaystyle 5\cdot 2^{25}+1}$
1886	Seelhoff	${\displaystyle F_{36}}$	${\displaystyle 5\cdot 2^{39}+1}$
1899	Cunningham	${\displaystyle F_{11}}$	${\displaystyle 39\cdot 2^{13}+1}$
1899	Cunningham	${\displaystyle F_{11}}$	${\displaystyle 119\cdot 2^{13}+1}$
1903	Western	${\displaystyle F_{9}}$	${\displaystyle 37\cdot 2^{16}+1}$
1903	Western	${\displaystyle F_{12}}$	${\displaystyle 397\cdot 2^{16}+1}$
1903	Western	${\displaystyle F_{12}}$	${\displaystyle 973\cdot 2^{16}+1}$
1903	Western	${\displaystyle F_{18}}$	${\displaystyle 13\cdot 2^{20}+1}$
1903	Cullen	${\displaystyle F_{38}}$	${\displaystyle 3\cdot 2^{41}+1}$
1906	Morehead	${\displaystyle F_{73}}$	${\displaystyle 5\cdot 2^{75}+1}$
1925	Kraitchik	${\displaystyle F_{15}}$	${\displaystyle 579\cdot 2^{21}+1}$

As of July 2023^[update], 368 prime factors of Fermat numbers are known, and 324 Fermat numbers are known to be composite. Several new Fermat factors are found each year.

Like composite numbers of the form 2^p − 1, every composite Fermat number is a strong pseudoprime to base 2. This is because all strong pseudoprimes to base 2 are also Fermat pseudoprimes – i.e.,

${\displaystyle 2^{F_{n}-1}\equiv 1{\pmod {F_{n}}}}$ 

for all Fermat numbers.

In 1904, Cipolla showed that the product of at least two distinct prime or composite Fermat numbers ${\displaystyle F_{a}F_{b}\dots F_{s},}$  ${\displaystyle a>b>\dots >s>1}$  will be a Fermat pseudoprime to base 2 if and only if ${\displaystyle 2^{s}>a}$ .

A Fermat number cannot be a perfect number or part of a pair of amicable numbers. (Luca 2000)

The series of reciprocals of all prime divisors of Fermat numbers is convergent. (Křížek, Luca & Somer 2002)

If nⁿ + 1 is prime, there exists an integer m such that n = 2^2m. The equation nⁿ + 1 = F_(2^m+m) holds in that case.

Let the largest prime factor of the Fermat number F_n be P(F_n). Then,

${\displaystyle P(F_{n})\geq 2^{n+2}(4n+9)+1.}$  (Grytczuk, Luca & Wójtowicz 2001)

 

Carl Friedrich Gauss developed the theory of Gaussian periods in his Disquisitiones Arithmeticae and formulated a sufficient condition for the constructibility of regular polygons. Gauss stated that this condition was also necessary, but never published a proof. Pierre Wantzel gave a full proof of necessity in 1837. The result is known as the Gauss–Wantzel theorem:

An n-sided regular polygon can be constructed with compass and straightedge if and only if n is either a power of 2 or the product of a power of 2 and distinct Fermat primes: in other words, if and only if n is of the form n = 2^k or n = 2^kp₁p₂...p_s, where k, s are nonnegative integers and the p_i are distinct Fermat primes.

A positive integer n is of the above form if and only if its totient φ(n) is a power of 2.

Pseudorandom number generation

Fermat primes are particularly useful in generating pseudo-random sequences of numbers in the range 1, ..., N, where N is a power of 2. The most common method used is to take any seed value between 1 and P − 1, where P is a Fermat prime. Now multiply this by a number A, which is greater than the square root of P and is a primitive root modulo P (i.e., it is not a quadratic residue). Then take the result modulo P. The result is the new value for the RNG.

${\displaystyle V_{j+1}=(A\times V_{j}){\bmod {P}}}$  (see linear congruential generator, RANDU)

This is useful in computer science, since most data structures have members with 2^X possible values. For example, a byte has 256 (2⁸) possible values (0–255). Therefore, to fill a byte or bytes with random values, a random number generator that produces values 1–256 can be used, the byte taking the output value −1. Very large Fermat primes are of particular interest in data encryption for this reason. This method produces only pseudorandom values, as after P − 1 repetitions, the sequence repeats. A poorly chosen multiplier can result in the sequence repeating sooner than P − 1.

Numbers of the form ${\displaystyle a^{2^{\overset {n}{}}}\!\!+b^{2^{\overset {n}{}}}}$  with a, b any coprime integers, a > b > 0, are called generalized Fermat numbers. An odd prime p is a generalized Fermat number if and only if p is congruent to 1 (mod 4). (Here we consider only the case n > 0, so 3 = ${\displaystyle 2^{2^{0}}\!+1}$  is not a counterexample.)

An example of a probable prime of this form is 1215¹³¹⁰⁷² + 242¹³¹⁰⁷² (found by Kellen Shenton).

By analogy with the ordinary Fermat numbers, it is common to write generalized Fermat numbers of the form ${\displaystyle a^{2^{\overset {n}{}}}\!\!+1}$  as F_n(a). In this notation, for instance, the number 100,000,001 would be written as F₃(10). In the following we shall restrict ourselves to primes of this form, ${\displaystyle a^{2^{\overset {n}{}}}\!\!+1}$ , such primes are called "Fermat primes base a". Of course, these primes exist only if a is even.

If we require n > 0, then Landau's fourth problem asks if there are infinitely many generalized Fermat primes F_n(a).

Generalized Fermat primes of the form F_n(a)

Because of the ease of proving their primality, generalized Fermat primes have become in recent years a topic for research within the field of number theory. Many of the largest known primes today are generalized Fermat primes.

Generalized Fermat numbers can be prime only for even a, because if a is odd then every generalized Fermat number will be divisible by 2. The smallest prime number ${\displaystyle F_{n}(a)}$  with ${\displaystyle n>4}$  is ${\displaystyle F_{5}(30)}$ , or 30³² + 1. Besides, we can define "half generalized Fermat numbers" for an odd base, a half generalized Fermat number to base a (for odd a) is ${\displaystyle {\frac {a^{2^{n}}\!+1}{2}}}$ , and it is also to be expected that there will be only finitely many half generalized Fermat primes for each odd base.

In this list, the generalized Fermat numbers (${\displaystyle F_{n}(a)}$ ) to an even a are ${\displaystyle a^{2^{n}}\!+1}$ , for odd a, they are ${\displaystyle {\frac {a^{2^{n}}\!\!+1}{2}}}$ . If a is a perfect power with an odd exponent (sequence A070265 in the OEIS), then all generalized Fermat number can be algebraic factored, so they cannot be prime.

See for even bases up to 1000, and for odd bases. For the smallest number ${\displaystyle n}$  such that ${\displaystyle F_{n}(a)}$  is prime, see OEIS: A253242.

${\displaystyle a}$	numbers ${\displaystyle n}$  such that ${\displaystyle F_{n}(a)}$  is prime	${\displaystyle a}$	numbers ${\displaystyle n}$  such that ${\displaystyle F_{n}(a)}$  is prime	${\displaystyle a}$	numbers ${\displaystyle n}$  such that ${\displaystyle F_{n}(a)}$  is prime	${\displaystyle a}$	numbers ${\displaystyle n}$  such that ${\displaystyle F_{n}(a)}$  is prime
2	0, 1, 2, 3, 4, ...	18	0, ...	34	2, ...	50	...
3	0, 1, 2, 4, 5, 6, ...	19	1, ...	35	1, 2, 6, ...	51	1, 3, 6, ...
4	0, 1, 2, 3, ...	20	1, 2, ...	36	0, 1, ...	52	0, ...
5	0, 1, 2, ...	21	0, 2, 5, ...	37	0, ...	53	3, ...
6	0, 1, 2, ...	22	0, ...	38	...	54	1, 2, 5, ...
7	2, ...	23	2, ...	39	1, 2, ...	55	...
8	(none)	24	1, 2, ...	40	0, 1, ...	56	1, 2, ...
9	0, 1, 3, 4, 5, ...	25	0, 1, ...	41	4, ...	57	0, 2, ...
10	0, 1, ...	26	1, ...	42	0, ...	58	0, ...
11	1, 2, ...	27	(none)	43	3, ...	59	1, ...
12	0, ...	28	0, 2, ...	44	4, ...	60	0, ...
13	0, 2, 3, ...	29	1, 2, 4, ...	45	0, 1, ...	61	0, 1, 2, ...
14	1, ...	30	0, 5, ...	46	0, 2, 9, ...	62	...
15	1, ...	31	...	47	3, ...	63	...
16	0, 1, 2, ...	32	(none)	48	2, ...	64	(none)
17	2, ...	33	0, 3, ...	49	1, ...	65	1, 2, 5, ...

For the smallest even base a such that ${\displaystyle F_{n}(a)}$  is prime, see OEIS: A056993.

${\displaystyle n}$	bases a such that ${\displaystyle F_{n}(a)}$  is prime (only consider even a)	OEIS sequence
0	2, 4, 6, 10, 12, 16, 18, 22, 28, 30, 36, 40, 42, 46, 52, 58, 60, 66, 70, 72, 78, 82, 88, 96, 100, 102, 106, 108, 112, 126, 130, 136, 138, 148, 150, ...	A006093
1	2, 4, 6, 10, 14, 16, 20, 24, 26, 36, 40, 54, 56, 66, 74, 84, 90, 94, 110, 116, 120, 124, 126, 130, 134, 146, 150, 156, 160, 170, 176, 180, 184, ...	A005574
2	2, 4, 6, 16, 20, 24, 28, 34, 46, 48, 54, 56, 74, 80, 82, 88, 90, 106, 118, 132, 140, 142, 154, 160, 164, 174, 180, 194, 198, 204, 210, 220, 228, ...	A000068
3	2, 4, 118, 132, 140, 152, 208, 240, 242, 288, 290, 306, 378, 392, 426, 434, 442, 508, 510, 540, 542, 562, 596, 610, 664, 680, 682, 732, 782, ...	A006314
4	2, 44, 74, 76, 94, 156, 158, 176, 188, 198, 248, 288, 306, 318, 330, 348, 370, 382, 396, 452, 456, 470, 474, 476, 478, 560, 568, 598, 642, ...	A006313
5	30, 54, 96, 112, 114, 132, 156, 332, 342, 360, 376, 428, 430, 432, 448, 562, 588, 726, 738, 804, 850, 884, 1068, 1142, 1198, 1306, 1540, 1568, ...	A006315
6	102, 162, 274, 300, 412, 562, 592, 728, 1084, 1094, 1108, 1120, 1200, 1558, 1566, 1630, 1804, 1876, 2094, 2162, 2164, 2238, 2336, 2388, ...	A006316
7	120, 190, 234, 506, 532, 548, 960, 1738, 1786, 2884, 3000, 3420, 3476, 3658, 4258, 5788, 6080, 6562, 6750, 7692, 8296, 9108, 9356, 9582, ...	A056994
8	278, 614, 892, 898, 1348, 1494, 1574, 1938, 2116, 2122, 2278, 2762, 3434, 4094, 4204, 4728, 5712, 5744, 6066, 6508, 6930, 7022, 7332, ...	A056995
9	46, 1036, 1318, 1342, 2472, 2926, 3154, 3878, 4386, 4464, 4474, 4482, 4616, 4688, 5374, 5698, 5716, 5770, 6268, 6386, 6682, 7388, 7992, ...	A057465
10	824, 1476, 1632, 2462, 2484, 2520, 3064, 3402, 3820, 4026, 6640, 7026, 7158, 9070, 12202, 12548, 12994, 13042, 15358, 17646, 17670, ...	A057002
11	150, 2558, 4650, 4772, 11272, 13236, 15048, 23302, 26946, 29504, 31614, 33308, 35054, 36702, 37062, 39020, 39056, 43738, 44174, 45654, ...	A088361
12	1534, 7316, 17582, 18224, 28234, 34954, 41336, 48824, 51558, 51914, 57394, 61686, 62060, 89762, 96632, 98242, 100540, 101578, 109696, ...	A088362
13	30406, 71852, 85654, 111850, 126308, 134492, 144642, 147942, 150152, 165894, 176206, 180924, 201170, 212724, 222764, 225174, 241600, ...	A226528
14	67234, 101830, 114024, 133858, 162192, 165306, 210714, 216968, 229310, 232798, 422666, 426690, 449732, 462470, 468144, 498904, 506664, ...	A226529
15	70906, 167176, 204462, 249830, 321164, 330716, 332554, 429370, 499310, 524552, 553602, 743788, 825324, 831648, 855124, 999236, 1041870, ...	A226530
16	48594, 108368, 141146, 189590, 255694, 291726, 292550, 357868, 440846, 544118, 549868, 671600, 843832, 857678, 1024390, 1057476, 1087540, ...	A251597
17	62722, 130816, 228188, 386892, 572186, 689186, 909548, 1063730, 1176694, 1361244, 1372930, 1560730, 1660830, 1717162, 1722230, 1766192, ...	A253854
18	24518, 40734, 145310, 361658, 525094, 676754, 773620, 1415198, 1488256, 1615588, 1828858, 2042774, 2514168, 2611294, 2676404, 3060772, ...	A244150
19	75898, 341112, 356926, 475856, 1880370, 2061748, 2312092, 2733014, 2788032, 2877652, 2985036, 3214654, 3638450, 4896418, 5897794, ...	A243959
20	919444, 1059094, 1951734, 1963736, ...	A321323

The smallest bases b=b(n) such that b²ⁿ + 1 (for given n= 0,1,2, ...) is prime are

2, 2, 2, 2, 2, 30, 102, 120, 278, 46, 824, 150, 1534, 30406, 67234, 70906, 48594, 62722, 24518, 75898, 919444, ... (sequence A056993 in the OEIS)

Conversely, the smallest k=k(n) such that (2n)^k + 1 (for given n) is prime are

1, 1, 1, 0, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 0, 4, 1, ... (The next term is unknown) (sequence A079706 in the OEIS) (also see OEIS: A228101 and OEIS: A084712)

A more elaborate theory can be used to predict the number of bases for which ${\displaystyle F_{n}(a)}$  will be prime for fixed ${\displaystyle n}$ . The number of generalized Fermat primes can be roughly expected to halve as ${\displaystyle n}$  is increased by 1.

Generalized Fermat primes of the form F_n(a, b)

It is also possible to construct generalized Fermat primes of the form ${\displaystyle a^{2^{n}}+b^{2^{n}}}$ . As in the case where b=1, numbers of this form will always be divisible by 2 if a+b is even, but it is still possible to define generalized half-Fermat primes of this type. For the smallest prime of the form ${\displaystyle F_{n}(a,b)}$  (for odd ${\displaystyle a+b}$ ), see also OEIS: A111635.

${\displaystyle a}$	${\displaystyle b}$	numbers ${\displaystyle n}$  such that ${\displaystyle F_{n}(a,b)={\frac {a^{2^{n}}+b^{2^{n}}}{\gcd(a+b,2)}}}$  is prime
2	1	0, 1, 2, 3, 4, ...
3	1	0, 1, 2, 4, 5, 6, ...
3	2	0, 1, 2, ...
4	1	0, 1, 2, 3, ... (equivalent to ${\displaystyle F_{n}(2,1)}$ )
4	3	0, 2, 4, ...
5	1	0, 1, 2, ...
5	2	0, 1, 2, ...
5	3	1, 2, 3, ...
5	4	1, 2, ...
6	1	0, 1, 2, ...
6	5	0, 1, 3, 4, ...
7	1	2, ...
7	2	1, 2, ...
7	3	0, 1, 8, ...
7	4	0, 2, ...
7	5	1, 4,
7	6	0, 2, 4, ...
8	1	(none)
8	3	0, 1, 2, ...
8	5	0, 1, 2,
8	7	1, 4, ...
9	1	0, 1, 3, 4, 5, ... (equivalent to ${\displaystyle F_{n}(3,1)}$ )
9	2	0, 2, ...
9	4	0, 1, ... (equivalent to ${\displaystyle F_{n}(3,2)}$ )
9	5	0, 1, 2, ...
9	7	2, ...
9	8	0, 2, 5, ...
10	1	0, 1, ...
10	3	0, 1, 3, ...
10	7	0, 1, 2, ...
10	9	0, 1, 2, ...
11	1	1, 2, ...
11	2	0, 2, ...
11	3	0, 3, ...
11	4	1, 2, ...
11	5	1, ...
11	6	0, 1, 2, ...
11	7	2, 4, 5, ...
11	8	0, 6, ...
11	9	1, 2, ...
11	10	5, ...
12	1	0, ...
12	5	0, 4, ...
12	7	0, 1, 3, ...
12	11	0, ...

Largest known generalized Fermat primes

The following is a list of the five largest known generalized Fermat primes. The whole top-5 is discovered by participants in the PrimeGrid project.

On the Prime Pages one can find the current top 100 generalized Fermat primes.

• Constructible polygon: which regular polygons are constructible partially depends on Fermat primes.
• Double exponential function
• Lucas' theorem
• Mersenne prime
• Pierpont prime
• Primality test
• Proth's theorem
• Pseudoprime
• Sierpiński number
• Sylvester's sequence