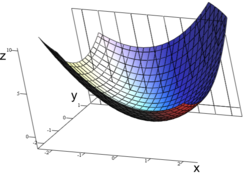
Đạo Hàm Riêng

Đạo hàm riêng được sử dụng trong giải tích vector và hình học vi phân.

Đạo hàm riêng của f đối với biến x được ký hiệu khác nhau bởi

${\displaystyle f_{x}^{\prime },\ f_{x},\ f_{,x},\ \partial _{x}f,{\text{ hoặc }}{\frac {\partial f}{\partial x}}}$

Ký hiệu của đạo hàm riêng là ∂. Ký hiệu này được giới thiệu bởi Adrien-Marie Legendre và được chấp nhận rộng rãi sau khi nó được giới thiệu lại bởi Carl Gustav Jacob Jacobi.

Đồ thị của hàm số z = x² + xy + y². Đạo hàm riêng tại điểm (1, 1, 3) với y là hằng số tương ứng với đường tiếp tuyến song song với mặt phẳng xz.

Mặt cắt của đồ thị trên tại y= 1

Ví dụ sau sẽ giúp giải thích định nghĩa của đạo hàm riêng theo biến y.Giả sử một hàm theo hai biến x,y được xem như là một họ các hàm theo y được đánh số theo x

${\displaystyle f(x,y)=f_{x}(y)=\,\!x^{2}+xy+y^{2}.\,}$ 

Nói một cách khác, mỗi giá trị của x định nghĩa một hàm số, ký hiệu là f_x, mà nó là hàm số một biến. Nghĩa là

${\displaystyle f_{x}(y)=x^{2}+xy+y^{2}.\,}$ 

Một khi giá trị của x được chọn, ví dụ là a, thì f(x,y) xác định một hàm số f_a

${\displaystyle f_{a}(y)=a^{2}+ay+y^{2}.\,}$ 

Trong công thức này, a là hằng số, không phải là biến số, do đó f_a là một hàm số một biến và do vậy ta có thể sử dụng định nghĩa đạo hàm cho hàm một biến:

${\displaystyle f_{a}'(y)=a+2y.\,}$ 

Quy trình trên có thể được áp dụng cho bất cứ lựa chọn nào của a. Khi đem gộp lại tất cả những đạo hàm đó ta có được sự biến thiên của hàm số f theo hướng của y:

${\displaystyle {\frac {\partial f}{\partial y}}(x,y)=x+2y.\,}$ 

Đây là đạo hàm riêng của f theo biến số y. Ổ đây ∂ được gọi là ký hiệu đạo hàm riêng.

Một cách tổng quát, đạo hàm riêng của một hàm số f(x₁,...,x_n) theo hướng x_i tại điểm (a₁,...,a_n) được định nghĩa là:

${\displaystyle {\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n})=\lim _{h\to 0}{\frac {f(a_{1},\ldots ,a_{i}+h,\ldots ,a_{n})-f(a_{1},\ldots ,a_{i},\dots ,a_{n})}{h}}.}$ 

Trong tỷ số bên trên, tất cả các biến ngoại trừ x_i được giữ cố định. Do vậy ta chỉ có hàm số theo một biến ${\displaystyle f_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}(x_{i})=f(a_{1},\ldots ,a_{i-1},x_{i},a_{i+1},\ldots ,a_{n})}$ , và do định nghĩa,,

${\displaystyle {\frac {df_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}}{dx_{i}}}(x_{i})={\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n}).}$ 

Một ví dụ quan trọng của đạo hàm riêng: Cho một hàm số f(x₁,...x_n) đinh nghĩa trên một miền của Rⁿ (ví dụ, trên R² hay là R³). Trong trường hợp này f có các đạo hàm riêng ∂f/∂x_j đối với mỗi biến x_j. Tại điểm a, những đạo hàm riêng này định ra vector

${\displaystyle \nabla f(a)=\left({\frac {\partial f}{\partial x_{1}}}(a),\ldots ,{\frac {\partial f}{\partial x_{n}}}(a)\right).}$ 

Vector này được gọi là gradient của f tại a. Nếu f khả vi tại mọi điểm trong một miền nào đó, thì gradient là hàm số có trị là vectơ ∇f đưa điểm a đến vectơ ∇f(a). Do đó gradient là một trường vectơ.

• Partial Derivatives trên MathWorld