ગણિત

ગણિતશાસ્ત્રની ચોક્કસ વ્યાખ્યા અને તેના વ્યાપ વિષે ગણિતજ્ઞો અને તત્વજ્ઞો જુદા જુદા વિચારો ધરાવે છે.

ગણિતજ્ઞો આસપાસથી સુંદર રચનાઓ ખોળે છે અને તેનો ઉપયોગ નવી ધારણાઓ બનાવવામાં કરે છે. તેઓ ગણિત પર આધારિત સાબિતી વડે આ ધારણાઓનું સત્યાર્થતા નક્કી કરે છે. જ્યારે ગણિતીય માળખાં વાસ્તવિક ઘટનાના બહુ સારા નમૂના હોય ત્યારે, ગણિતીય સમજ આપણને કુદરત વિશે આંતરદૃષ્ટિ અને આગાહીઓ પૂરી પાડે છે.

અમૂર્ત પૃથ્થકરણ અને તર્કનો ઉપયોગ કરીને ગણના, ગણત્રી, માપણીથી શરૂઆત કરીને નિષ્કરણ અને તર્કશાસ્ત્ર ગણિતના વિકાસના મુખ્ય પડાવો છે. અહીંથી આગળ વિકાસ પામીને, ગણિતશાસ્ત્ર છેક ભૌતિક વસ્તુઓના આકાર અને ગતિઓના પધ્ધતિસરના અભ્યાસનું શાસ્ત્ર બન્યું. ભૂતકાળની જ્યાં સુધીની લેખિત નોંધ અસ્તિત્વમાં છે, ત્યારથી વ્યવહારિક ગણિત માનવીય પ્રવૃતિનો એક ભાગ જ રહ્યું છે. ગણિતશાસ્ત્રના કોયડાઓ ઉકેલવા માટે જરુરી શોધ વર્ષો, કે ક્યારેક સદીઓની, સતત જહેમત માગી લે છે.

ગણિતશાસ્ત્ર અંગેની ઉગ્ર દલીલો સહુ પ્રથમ ગ્રીક ગણિતશાસ્ત્રમાં જોવા મળે છે, તેમાં પણ નોંધપાત્ર રીતે યુક્લિડના "એલિમેન્ટસ"માં. ગ્યુસેપ પીનો (૧૮૫૮-૧૯૩૨ ), ડેવિડ હિલ્બર્ટ (૧૮૬૨-૧૯૪૩ ) અને બીજા ગણિતજ્ઞોએ ૧૯મી સદીના ઉતરાર્ધમાં, ધારણાત્મક પધ્ધતિ પરનાં શરુઆતનાં પાયાનાં કાર્યો કર્યા. એ સમયથી હવે એ રિવાજ થઈ ગયો છે કે ગણિતના ક્ષેત્રની કોઈ શોધ એટલે, યોગ્ય રીતે પસંદ કરેલાં સ્વયંસિદ્ધ સિદ્ધાંતો અને વ્યાખ્યાઓ પરથી મહેનત કરીને તારતમ્યો વડે સત્ય પ્રસ્થાપિત કરવું. નવજાગૃતિના સમયખંડસુધી ગણિતના ક્ષેત્રનો વિકાસ પ્રમાણમાં ધીમી ગતિએ થયો. ત્યાર પછીથી નવી વૈજ્ઞાનિક શોધો સાથે સંવાદ સધાતાં થતી ગણિતની શોધની ઝડપની માત્રામાં ત્વરિત વધારો થયો, જે આજ સુધી ચાલુ છે.

ગેલિલિયો ગેલિલી (૧૫૬૪-૧૬૪૨) એ કહ્યું હતું, "જ્યાં સુધી આપણે ભાષા ન શીખીએ અને તેની લિપિમાં વપરાતાં ચિન્હોની ઓળખ ન મેળવીએ, ત્યાં સુધી બ્રહ્માંડને વાંચી ન શકીએ. બ્રહ્માંડ ગણિતની ભાષામાં લખાયેલું છે. ત્રિકોણ, વર્તુળ અને બીજાં ભૌમિતિક ચિત્રો તેના અક્ષરો છે, જેના સિવાય બ્રહ્માંડ વિષે એક પણ શબ્દ સમજવો મણસને માટે અશક્ય છે. એ બધા વિના તો અંધારા ભોંયરામાં અટવાવા જેવું છે." કાર્લ ફ્રેડરિક ગોસ (૧૭૭૭-૧૮૫૫) ગણિતશાસ્ત્રને, "વિજ્ઞાન જગતની રાણી" કહ્યું છે. બેન્જામિન પીર્સે (૧૮૦૯-૧૮૮૦) ગણિતને, “જરુરી તારતમ્યો મેળવનાર વિજ્ઞાન" તરીકે ઓળખાવ્યું છે. ડેવિડ હિલ્બર્ટે ગણિત વિષે કહે છે કે, " અહીં આપણે કોઈ રીતના નિયમહીનપણાની વાત ક્યારેય કરતા નથી. ગણિત એ કોઈ એવી રમત નથી કે જેમાં મનસ્વીપણે નિયત કરેલા કાયદા પ્રમાણે તેનાં કામ નક્કી થાય. એ તો આંતરિક જરુરિયાત ધરાવતી એક વિચારપધ્ધતિ છે, જે આવી જ હોઈ શકે અને ક્યારેય કંઈ અલગ નહીં." આલ્બર્ટ આઈન્સ્ટાઈને (૧૮૭૯-૧૯૫૫) કહ્યું છે કે, "જ્યાં સુધી ગણિતના નિયમો વાસ્તવિકતા સાથે સંબંધિત છે, ત્યારે તે ચોક્કસ નથી હોતા. અને જ્યાં સુધી તે ચોક્કસ છે, ત્યારે તે વાસ્તવિકતા સંબંધિત નથી હોતા." ફ્રેન્ચ ગણિતશાસ્ત્રી ક્લેર વોઈઝિને કહ્યું છે, "ગણિતશાસ્ત્રમાં એક સર્જનાત્મક ધગશ છે. પોતાને વ્યક્ત કરવાના પ્રયત્નની ચળવળ વિષેનું શાસ્ત્ર છે." આખા વિશ્વમાં કુદરતી વિજ્ઞાન, તંત્રવિદ્યા, તબીબી વિદ્યા, નાણાંશાસ્ત્ર અને સમાજવિદ્યા જેવાં ઘણાં ક્ષેત્રોમાં, ગણિતશાસ્ત્રને એક જરુરી સાધન તરીકે વાપરવામાં આવે છે. ગણિતશાસ્ત્રની એવી શાખા કે જેને બીજાં ક્ષેત્રોમાં ગણિતના જ્ઞાનને વાપરવા સાથે સંબંધ છે, તે પ્રયોજિત ગણિતશાસ્ત્ર તરીકે ઓળખાય છે. તે નવી ગણિતીય શોધોને પ્રેરે છે અને તેનો ઉપયોગ કરે છે. આને કારણે આંકડાશાસ્ત્ર અને ગેઈમ થિયરી જેવી સંપૂર્ણપણે નવી જ ગણિત વિદ્યાશાખાઓનો વિકાસ થયો. ગણિતના જ્ઞાનના કોઈ પણ ઉપયોગોની ચિંતા કર્યા સિવાય પણ ગણિતશાસ્ત્રીઓ શુધ્ધ ગણિતશાસ્ત્રના અભ્યાસમાં ઓતપ્રોત રહે છે એટલે કે ગણિતનો અભ્યાસ તે વિષયના પોતાના આનંદ ખાતર કરે છે. "શુધ્ધ ગણિત" અને "પ્રયોજિત ગણિત" વચ્ચે એવી કોઈ સ્પષ્ટ ભેદરેખા નથી. ઘણી વખત એવું પણ બને છે કે શુધ્ધ ગણિતનાં જ્ઞાન તરીકે શરુ થયેલા અભ્યાસનો પાછળથી બીજે ઉપયોગો મળે છે.

 

બે સફરજન અને બે સંતરા વચ્ચે કંઈક સામ્યતા છે (તેમની સંખ્યા) એ સમજણ માણસની વિચારશક્તિના વિકાસમાં એક હરણફાળ હતી. આ સમજણ વડે માનવ દરેક પ્રશ્નને અલગ અલગ વિચારતો થયો અને દરેક હેતુમાંથી જરૂરી સંકલ્પનાઓ તારવતો થયો અને આમ ગણિતનો વિકાસ થતો ગયો.

 

ગણિતશાસ્ત્રની ઉત્ક્રાંતિને આપણે, હંમેશાં વધતાં રહેતાં અમૂર્ત પ્રુથક્કરણની શ્રેણી તરીકે અથવા વિષયવસ્તુનાં વિસ્તરણ તરીકે જોઈ શકીએ.પ્રથમ પ્રુથક્ક્રરણ કદાચ સંખ્યાઓનું હતું, જેમાં પ્રાણીઓ પણ સહભાગી હતાં. દા. ત. એ ખ્યાલ કે બે સફરજનના સમૂહ અને બે નારંગીના સમૂહ વચ્ચે કંઈક સરખાપણું છે, જે તે બન્નેમાં રહેલી વસ્તુઓનો જથ્થો છે.

ભૌતિક વસ્તુઓની ગણતરી કેમ કરવી તે સમજવા ઉપરાંત, હાડકાં પર મળેલી ગણતરીરેખાઓ વડે સાબિત થાય છે કે ,પ્રાગૈતિહાસિક માનવોએ સમય- દિવસો, ઋતુઓ, વર્ષો જેવા અમૂર્ત જથ્થા ની ગણતરીની સમજ પણ કેળવી હશે.

ઈ. સ. પૂર્વે ૩૦૦૦ આસપાસ સુધી વધારે જટિલ ગણિતશાસ્ત્ર અસ્તિત્વમાં નહોતું. એ પછી, બેબિલોન અને ઈજીપ્તના લોકોએ, મહેસુલ અને બીજી નાણાકીય ગણતરીઓ,મકાનોનાં બાંધકામ અને ખગોળશાસ્ત્ર માટે અંકગણિત, બીજગણિત અને ભૂમિતિનો ઉપયોગ શરુ કર્યો. વ્યાપાર, જમીનની માપણી, ભાતનાં ચિત્રકામ અને વણાટની ગુંથણી અને સમયની નોંધ રાખવા માટે સૌથી વહેલો ગણિતનો ઉપયોગ થયો.

પુરાતત્વશાસ્ત્રની નોંધમાં સૌથી પહેલાં બેબિલોનનાં ગણિતશાસ્ત્રમાં પ્રાથમિક ગણિત (સરવાળા, બાદબાકી, ગુણાકાર, ભાગાકાર) દેખાય છે. લખાણથી પહેલાં સંખ્યાજ્ઞાન અસ્તિત્વમાં હતું, ઘણી અને જાતજાતની સંખ્યાપધ્ધ્તિઓ અસ્તિત્વમાં છે. ર્હિન્ડ મેથેમટિકલ પેપિરસ જેવાં મધ્ય રાજ્ય લખાણોમાં ઈજીપ્શિયનોએ, આપણી જાણ મુજબ, સૌ પ્રથમ લખેલી સંખ્યાઓ બનાવી. [citation needed]

પ્રાચીન ગ્રીક લોકોએ, ઈ.સ. પૂર્વે ૬૦૦ થી ઈ. સ. પૂર્વે ૩૦૦ ની વચ્ચે ગ્રીક ગણિતશાસ્ત્ર વડે, રીતસરના અભ્યાસ તરીકે ગણિતશાસ્ત્રનો પધ્ધતિસરનો અભ્યાસ કર્યો. એ સમય પછી ગણિતશાસ્ત્ર અતિ વિકસ્યું છે અને વિજ્ઞાન અને ગણિત વચ્ચેનો ફળદાયી સંવાદ સધાયો છે, જે બંને માટે લાભદાયક નીવડ્યો છે. ગણિતીય શોધો આજ સુધી ચાલુ રહી છે. ‘બુલેટીન ઓફ ધ અમેરિકન મેથેમેટીકલ સોસાયટી’ના જાન્યુઆરી ૨૦૦૬ ના અંકમાં મિખાઈલ બ. સેવ્ર્યુકના મત મુજબ, " ઈ. સ. ૧૯૪૦માં મેથેમેટીકલ રીવ્યુસના ચાલુ થયાના પ્રથમ વર્ષથી અત્યાર સુધીના મેથેમેટીકલ રીવ્યુસના માહિતિફલક પર ૧૯ લાખથી વધારે પત્રો અને પુસ્તકોનો સમાવેશ થયો છે. દર વર્ષે આ માહિતિફલક પર ૭૫ હજાર વધારે આવાં લખાણોનો ઉમેરો થાય છે.આ મહાસાગરમાંનાં મોટા ભાગનાં કાર્યોની અંદર નવાં ગણિતીય પ્રમેયો અને તેની સાબિતિઓ છે.

મેથેમેટિક્સ શબ્દ ગ્રીક શબ્દ (mathema) પરથી આવ્યો છે.પ્રાચીન ભાષામાં તેના અર્થ, " જે શીખવામાં આવે છે તે ", "જેની કોઈ જાણકારી મેળવે છે તે",અને તેથી "અભ્યાસ" અને " વિજ્ઞાન" થાય છે. આધુનિક ગ્રીક ભાષામાં તેનો અર્થ માત્ર " પાઠ" થાય છે. mathema શબ્દ mathaino પરથી આવ્યો છે.જ્યારે, અર્વાચીન ગ્રીક ભાષામાં તેનો સમાનાર્થી શબ્દ mathaino છે.આ બન્નેનો અર્થ "શીખવું" થાય છે.ગ્રીસમાં, બહુ પ્રાચીન સમયમાં પણ, " મેથેમેટિક્સ" શબ્દનો વધારે સાંકડો અને વધારે શાસ્ત્રીય અર્થ " ગણિતનો અભ્યાસ" થયો.એનું વિશેષણ(mathēmatikós) છે, જેનો અર્થ થાય છે " જ્ઞાન સંબંધી" અથવા "અભ્યાસુ". એનો અર્થ આ રીતે જ આગળ ઉપર ગણિતીય (મેથેમેટિકલ \ mathematical) થયો.ખાસ કરીને, mathēmatikḗ tékhnē), લેટિન ભાષામાં આર્સ મેથેમેટિકા\ ars mathematica શબ્દનો અર્થ " ગણિતીય કળા" થયો.

લગભગ ઈ. સ. ૧૭૦૦ સુધી લેટિન અને અંગ્રેજી ભાષામાં "મેથેમેટિક્સ" નો સર્વસામાન્ય અર્થ "ગણિતશાસ્ત્ર" કરતાં, " જ્યોતિષશાસ્ત્ર" ( ક્યારેક “ખગોળશાસ્ત્ર ") થતો હતો. આ અર્થ છેવટે ઈ.સ. ૧૫૦૦ થી ઈ. સ. ૧૮૦૦ના સમયથી તેના વર્તમાન અર્થ ના રુપમાં બદલાયો. આન પરિણામે કેટલીક ગેરમાન્યતાઓ થઈ. સેંટ ઓગસ્ટાઈન દ્વાર અપાયેલી ચેતવણી, "ખ્રિસ્તી લોકોએ મેથેમેટિકી એટલે કે જ્યોતિષશાસ્ત્રીઓથી ચેતતા રહેવું " એ તો ખાસ કુખ્યાત છે. એને ગણિતશાસ્ત્રીઓને વખોડી કાઢવાની વાત તરીકે ગેરમાન્યતા મળે છે.

દેખીતી રીતે અંગ્રેજી ભાષામાં બહુવચનનાં રુપનું મૂળ, તેના ફ્રેંચ ભાષાના બહુવચનના રુપ les mathématiques ની જેમ (અને બહુ વપરાતાં, તારેવલ એકવચન la mathématique), છેક લેટિન ભાષાના નાન્યતર બહુવચન mathematica (Cicero )માં છે.એ શબ્દ પોતે પણ ગ્રીક બહુવચન ta mathēmatiká પર આધારિત છે..એનો ઉપયોગ એરિસ્ટોટલે ( ઈ.સ. પૂર્વે ૩૮૪ - ઈ.સ. પૂર્વે ૩૨૨ ) કર્યો અને તેનો ઉપરછલ્લો અર્થ " ગણિતને લગતું બધું જ " થતો હતો. તેમ છતાં એ તર્કસંગત છે કે અંગ્રેજી ભાષાએ વિશેષણ mathematic(al) ઉછીનું લીધું અને તેના પરથી, physics અને metaphysics ની જેમ mathematics એવું એકવચન નામ બનાવ્યું. ફિઝિક્સ અને મેટાફિઝિક્સ ગ્રીક વારસામાં મળેલાં છે. Mathematics એ નામવાચી શબ્દને ટૂંકા સ્વરુપે maths અને ઉત્તર અમેરિકામાં બોલાતી અંગ્રેજી ભાષામાં math કહે છે.

 

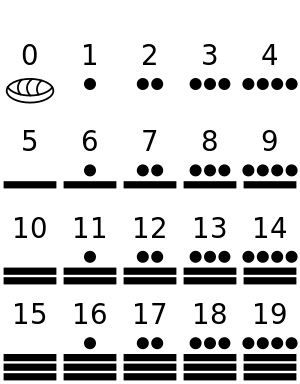
પ્રાગૈતિહાસિક માનવને મૂર્ત વસ્તુઓની ગણતરી કરતા આવડવા ઉપરાંત અમૂર્ત વસ્તુઓ જેમ કે સમય -- દિવસો, ઋતુઓ, વર્ષો વગેરેની ગણતરી કરતા પણ આવડતું હતું. ગણતરી કરવાનું આવડવાથી ધીરે ધીરે માનવી અંકગણિત - સરવાળા, બાદબાકી,ગુણાકાર અને ભાગાકાર - પણ શીખી ગયો. આ સુસ્પષ્ટ છે કે ફક્ત ગણતરી કરવાથી કે સરવાળા બાદબાકી કરવાથી જ ગણિતનો વિકાસ થયો નથી પરંતુ આંકડાઓ અને તેમની કિંમતો સ્પષ્ટ થયા પછી ખરેખરુ ગણિત વિકાસ પામ્યું છે. કદાચ આપણાં વડવાઓએ કોઇ દિવસ દિવાલ કે લાકડુ ખોતરીને પહેલો આંકડો પાડ્યો હશે.

ઐતિહાસિક વિગતો પરથી જાણવા મળ્યું છે કે, મુખ્ય ભણવાના વિષયોમાં ગણિતનો પ્રયોગ કરવો પડતો હતો જેમકે વ્યાપાર-વાણીજ્ય, જમીનની માપણી અને ખગોળ શાસ્ત્ર. આ ત્રણેય જરૂરિયાતોને લીધે ગણિતનો વિકાસ થયો જેને મોટા મોટા ત્રણ ભાગમાં વહેંચી શકાય: "માળખુ", "સ્થાન" અને "બદલાવ".

ઇ.સ્.પૂર્વે ૧૦૦૦ અને ઇ.સ્. ૧૦૦૦ વચ્ચે લખાયેલાં વિવિધ સંદર્ભોમાં પ્રથમ વખત ભારતતીય ગણિત શાસ્ત્રીઓએ શૂન્ય, બીજ ગણિત, પ્રમેયો (ગણતરી માટેનાં વિવિધ નિયમો), સંખ્યાઓનાં વર્ગમૂળ અને ઘનમૂળ, વિગેરેનો ઉપયોગ કર્યાનાં ઉલ્લેખો છે. જેને વૈદિક ગણિત તરીકે ઓળખવામાં આવે છે, અને આ વૈદિક ગણિત આજે પણ ભારત બહારની ઘણી બધી કોલેજો અને યુનિવર્સિટીઓમાં શિખવવામાં આવે છે.

એરિસ્ટોટલે ગણિતશાસ્ત્રની વ્યાખ્યા, " જથ્થાનું વિજ્ઞાન " તરીકે આપી, જે ૧૮મી સદી સુધી ચાલતી હતી. ૧૯મી સદીની શરુઆતમાં ગણિતશાસ્ત્રનો અભ્યાસ વધારે કઠિન થયો.જેને જથ્થા કે માપણી સાથે કોઈ ચોક્ખો સંબંધ નથી તેવા, "સમૂહના સિધ્ધાંતનુ શાસ્ત્ર" (Group Theory) અને " પ્રક્ષેપાત્મક ભૂમિતિ " (Projective Geometry) જેવા અમૂર્ત વિષયો હાથમાં લેવાના શરુ થયા. તે વખતે, ગણિતશાસ્ત્રીઓ અને તત્વવેતાઓએ જુદી જુદી જાતની નવી વ્યાખ્યાઓ સૂચવવાનું શરુ કર્યું આમાંની કેટલીક વ્યાખ્યાઓ ગણિતના તારતમ્ય કાઢવાના લક્ષણ પર ભાર મૂકતી હતી, તો બીજી કેટલીક તેની અમૂર્તતા પર ભાર મૂકતી હતી. તે ઉપરાંત કેટલીક તેની અંદર રહેલા ચોક્કસ વિષયો પર ભાર મૂકતી હતી. આજે, જાણકાર વિદ્વાનોમાં પણ ગણિતની વ્યાખ્યા વિષે સર્વસંમતિ સધાઈ નથી. એટલું જ નહીં, ગણિતશાસ્ત્ર એ વિજ્ઞાન છે કે કલા છે એ બાબતમાં પણ સર્વસંમતિ સધાઈ નથી. વિદ્વાન ગણિતશાસ્ત્રીઓનો એક મોટો વર્ગ ગણિતની વ્યાખ્યા બાબતમાં રસ લેતો નથી, અથવા એમ માને છે કે તેની વ્યાખ્યા બાધી શકાય તેમ નથી.કેટલાક માત્ર એમ કહે છે, "ગણિતશાસ્ત્રીઓ જે કરે છે તેને ગણિતશાસ્ત્ર કહેવાય."

ગણિતશાસ્ત્રની વ્યાખ્યાના ત્રણ મુખ્ય પ્રકારો, તર્કશાસ્ત્રીય, અંતઃપ્રેરણાકીય અને રુઢિચુસ્ત કહેવાય છે, જે જુદી જુદી તાત્વિક વિચારસરણી દર્શાવે છે. બધી વ્યાખ્યાઓને તેની સમસ્યાઓ છે, કોઈને સર્વવ્યાપી સંમતિ નથી મળી,અને એમાં કોઈ સમાધાન શક્ય નથી દેખાતું.

તર્કશાસ્ત્રની દૃષ્ટિએ શરુઆતના સમયની ગણિતની વ્યાખ્યા બેંજામિન પિયર્સે, ઈ. સ. ૧૮૭૦ માં, "જરુરી તારણો મેળવી આપતું વિજ્ઞાન" તરીકે આપી. "પ્રિંસિપા મેથેમેટિકા" માં બર્ટ્રાંડ રસેલ અને ઓલ્ફ્રેડ નોર્થ વ્હાઈટહેડે તર્કવાદ તરીકે જાણીતો કાર્યક્રમ આગળ વધાર્યો. એમણે એવું સાબિત કરવાના પ્રયત્નો કર્યા કે ગણિતના બધા જ વિચારો, વિધાનો અને સિધ્ધાંતો, સંપૂર્ણપણે સાંકેતિક તર્કશાસ્ત્રથી જ વ્યાખ્યાયિત અને સાબિત થઈ શકે છે.રસેલની "ગણિત એટલે માત્ર સાંકેતિક તર્કશાસ્ત્ર" (૧૯૦૩), એ ગણિતની તર્કવાદી વ્યાખ્યા છે.

ગણિતશાસ્ત્રી એલ. ઈ. જે. બ્રાઉવર ના વિચારોમાંથી વિકસેલી અંતઃપ્રેરણાકીય વ્યાખ્યાઓ, ગણિતને ચોક્કસ માનસિક ઘટનાઓ વડે ઓળખાવે છે.અંતઃપ્રેરણાકીય વ્યાખ્યાનો એક દાખલો - "ગણિત એક એવી માનસિક પ્રવ્રુતિ છે જેમાં એક પછી એક માળખાંનો અભ્યાસ થાય છે." [31] અંતઃપ્રેરણાવાદની વિચિત્રતા એ છે કે, બીજી વ્યાખ્યાઓ પ્રમાણે જે ગણિતીય વિચારોને સ્વીક્રુત ગણવામાં આવે છે, તેને એ નકારી કાઢે છે. ગણિતનાં બીજાં તત્વશાસ્ત્રો, એવા સિધ્ધાંતોને ગણિતમાં શામેલ કરે છે કે જેનું અસ્તિત્વ સાબિત કરી શકાય છે, ભલે તેને ઘડી શકાતા ન હોય.જ્યારે અંત;પ્રેરણાવાદ ફક્ત એવા જ ગણિતીય સિધ્ધાંતોને શામેલ કરે છે જેને ઘડી શકાય છે.

રુઢિચુસ્ત વ્યાખ્યાઓ ગણિતને તેના સંકેતો અને તેના પર કાર્ય કરવાના નિયમોથી ઓળખાવે છે. હસ્કેલ કરી એ "પ્રણાલિકા પર આધારિત માળખાંનું વિજ્ઞાન "જેવી સીધી સાદી વ્યાખ્યા આપી છે. પ્રણાલિકા પર આધારિત માળખું એટલે સંકેતોનો સમૂહ અથવા ચિન્હો, અને આ ચિન્હોને ભેગાં કરીને.એમાંથી સૂત્રો કેમ બનાવી શકાય તેના નિયમો.પ્રણાલિકાગત માળખાંમાં સત્યો (Axioms) નો અર્થ તેના સામાન્ય અર્થ, "સ્વયંસિદ્ધ સત્ય " થી જુદો છે.આ માળખાંમાં સત્ય એટલે તેમાંનાં એવાં ચિન્હોનો સમૂહ છે કે જેને એમાંના નિયમો પરથી પ્રતિપાદિત કરવાની જરુર નથી પડતી.

 

 

આઈઝેક ન્યૂટન (ડાબે) અને ગોટ્ફ્રિડ વિલ્હેમ લીબનિટ્ઝ (જમણે), જેમણે અતિસૂક્ષ્મ કલનશાસ્ત્રનો વિકાસ કર્યો

જ્યારે જ્યારે પ્રશ્ન તર્કની કસોટીએ ચડે છે ત્યારે ત્યારે ગણિત પ્રશ્નનો ઉત્તર આપવા આગળ આવે છે. શરુઆતમાં કૃષિ, વ્યાપાર, માપણી તથા અન્ય રોજબરોજની પ્રવૃત્તિઓમા ગણિતનો ઊપયોગ થતો હતો જે ધીરે ધીરે વૈજ્ઞાનીક પધ્ધતિ રુપે વિકસિત થયું છે.

આજે, ગણિતશાસ્ત્રીઓ જે કંઈ અભ્યાસ કરે છે તેનો ઉલ્લેખ વિજ્ઞાનની લગભગ બધી જ શાખાઓમાં થતો જોવા મળે છે. કેટલીક સમસ્યાઓ તો તેના પોતાના અભ્યાસમાંથી સર્જાય છે, દા. ત. ગણિતશાસ્ત્રની સમજ અને ભૌતિકશાસ્ત્રના દૃષ્ટિકોણને એકત્ર કરીને તેનો ઉપયોગ , ભૌતિકશાસ્ત્રી રિચર્ડ ફીમને ક્વોન્ટમ મિકેનિક્સનાં , પાથ ઈન્ટિગ્રલ ફોર્મ્યુલેશનની શોધ કરી. જ્યારે, કુદરતનાં ચાર મૂળભૂત બળોને એક કરવાનો પ્રયત્ન કરતી, હજી વિકસવાના તબક્કામાં છે તેવી સ્ટ્રિંગ થિયરી, નવા ગણિતને પ્રેરણા આપતી રહે છે. કેટલુંક ગણિત તેને જે ક્ષેત્રમાંથી પ્રેરણા મળી હોય , તે ક્ષેત્ર પૂરતુ જ પ્રસ્તુત છે, અને તે ક્ષેત્રની આગળની સમસ્યાઓને ઉકેલવા માટે વપરાય છે. પણ,ઘણી વખત એક ક્ષેત્રમાંથી પ્રેરિત થયેલુ ગણિત,બીજાં ઘણાં ક્ષેત્રોમાં ઉપયોગી સાબિત થાય છે, અને ગણિતીય સિધ્ધાંતોના સામાન્ય પુરવઠામાં જોડાઈ જાય છે. શુધ્ધ ગણિત અને પ્રયોજિત ગણિત વચ્ચે ઘણી વખત જુદાપણુ બતાવવામાં આવે છે.તેમ છતાં,શુધ્ધ ગણિતના વિષયોના ક્યારેક ઉપયોગો નીકળી આવે છે.દા. ત. સંકેતલિપિશાસ્ત્રમાં સંખ્યાશાસ્ત્રનો ઉપયોગ,.શુધ્ધ ગણિતશાસ્ત્રના ક્યારેક વ્યાવહારિક ઉપયોગો પણ નીકળી આવે છે એ નોંધનીય હકીકત છે. તેને યુજીન વિગ્નેર "ગણિતશાસ્ત્રનૉ અગમ્ય પ્રભાવ" કહે છે. વિજ્ઞાનપ્રધાન યુગમાંથયેલા જ્ઞાનના વિસ્ફોટથી, અભ્યાસનાં મોટા ભાગના ક્ષેત્રોની જેમ જ અહીં પણ વિશેષજ્ઞાન મેળવવાનું થયું છે. આજે ગણિતમાં સેંકડો વિશેષ અભ્યાસનાં ક્ષેત્રો અસ્તિત્વમાં છે અને "ગણિતશાસ્ત્રના વિષયોનું વર્ગીકરણ" ની છેલ્લી યાદી ૪૬ પાના પર પથરાયેલી છે. પ્રયોજિત ગણિતશાસ્ત્રના કેટલાંક ક્ષેત્રો ગણિત બહારની સંબંધિત પ્રણાલિઓમાં જોડાઈ ગયાં છે અને પોતે સ્વતંત્ર અભાસક્ષેત્ર તરીકે બહાર આવ્યાં છે. જેમાં આંકડાશાસ્ત્ર, ઓપરેશન્સ રિસર્ચ અને કમ્પ્યુટર વિજ્ઞાન આવે છે. જ્યોર્જ બુલ દ્વારા શોધાયેલ અને બુલીય બીજગણિત તરીકે ઓળખાતી ગણિતની શાખા છે, જેના કારણે કમ્પ્યુટરમાં સરકીટમાં ઉપયોગમાં લેવાય છે. બુલીય બીજગણિત સિવાય કમ્પ્યુટરની કલ્પના પણ શક્ય નહોતી.

જે લોકોનાં મનનો ઝોક ગણિત તરફ છે, તેમને માટે ગણિતમાંના ઘણા ભાગોનું એક ચોક્કસ સૌંદર્ય હોય છે. ઘણા ગણિતશાસ્ત્રીઓ તેનામાં રહેલી સુઘડતાની, તેમાં રહેલી આંતરિક કલાત્મકતાની અને અંદરની સુંદરતાની વાત કરે છે. અહીં સાદાઈ અને સામાન્યતાની કિંમત છે. અહીં સાદી અને સુઘડ સાબિતીની સુંદરતા છે, જેમકે "અવિભાજ્ય સંખ્યાઓ અનંત છે." એ હકિકતની યુક્લિડએ આપેલી સાબિતી. બીજું ઉદાહરણ "ફાસ્ટ ફોરીયર ટ્રાન્સફોર્મેશન " જેવી સુઘડ આંકડાકીય પધ્ધતિ કે જે ગણતરીને ખૂબ ઝડપી બનાવે છે. આ કલાત્મકતાની દૃષ્ટિ જ શુધ્ધ ગણિતના અભ્યાસને યથાર્થ ઠેરવવા માટે પૂરતી છે. આ માન્યતા, જી. એચ. હાર્ડીએ પોતાનાં પુસ્તક "એ મેથેમેટિશિયન્સ એપોલોજી" માં વ્યક્ત કરી છે. તેમણે ગણિતશાસ્ત્રની સુંદરતામાં ફાળો આપતાં પરિબળો, મહત્વ, અણધારેલાપણું, અનિવાર્યતા, અને કરકસર જેવાં માપદંડોને ઓળખી કાઢ્યા છે. ગણિતજ્ઞો હંમેશા ખાસ કરીને સુઘડ સાબિતીઓ શોધવા ખૂબ પ્રયત્ન કરે છે. ગણિતજ્ઞ પૌલ એર્ડોના શબ્દોમાં "ઈશ્વરીય પુસ્તક" માંથી આવી સાબિતીઓ મળે છે. ઘણા લોકો ગણિતીય કોયડાઓ ઉકેલવામાં જે આનંદ મેળવે છે તે મનોરંજક ગણિતશાસ્ત્રની લોકપ્રિયતાની બીજી નિશાની છે.

 

૧૬મી સદી સુધી તો આજનાં ગણિતમાં વપરાતા મોટા ભાગના સંકેતો શોધાયા નહોતા. એ પહેલાં ગણિતને પણ શબ્દોમાં લખવામાં આવતું હતું. આ બહુ મહેનત માંગી લેતી રીત હતી, જેને કારણે ગણિતિય વિકાસ મર્યાદીત રહ્યો હતો. આજે પ્રચલિત ઘણા સંકેતો ગણિતશાસ્ત્રી યુલર (૧૭૦૭-૧૭૮૩) એ આપ્યા.આધુનિક સંકેતલિપિ, વ્યાવસાયિક વર્ગને માટે ગણિતને ઘણું સરળ બનાવે છે, પણ શીખવાની શરુઆત કરનારા વર્ગને એ મુશ્કેલ લાગે છે. બહુ થોડા સંકેતોમાં ખૂબ મોટા પ્રમાણમાં ઠાંસીને ભરેલી માહિતિ એટલે આધુનિક સંકેતશાસ્ત્ર. સંગીતશાસ્ત્રના સંકેતોની જેમ જ આધુનિક ગણિતના સંકેતોનું એક કડક બંધારણ છે, (જે અમુક હદે એક લેખકથી બીજા લેખક કે ગણિતની એક શાખાથી બીજી શાખા વચ્ચે થોડું બદલે છે.)જે માહિતીને બીજી કોઈ રીતે લખવાનું મુશ્કેલ હોય તે માહિતીને સંકેતોમાં બદલે છે.

 

શીખવાની શરુઆત કરનારા માટે ગણિતની ભાષા સમજવી કઠણ હોઈ શકે છે. અથવા (or) અને માત્ર (only) જેવા શબ્દોના રોજની બોલચાલની ભાષામાં જે અર્થ થાય તેના કરતાં ગણિતમાં બહુ ચોક્કસ અર્થ થાય છે. એ ઉપરાંત ખુલ્લું (open ) કે ક્ષેત્ર (field) જેવા શબ્દોને ગણિતની ભાષામાં બહુ આગવા અર્થ માટે લેવામાં આવ્યા છે. હોમીયોમૉરફીઝમ(homeomorphism) અને સંકલિત થઈ શકે તેવું (integrable) જેવા શાસ્ત્રીય શબ્દોને ગણિતમાં બહુ ચોક્કસ અર્થ છે. પહેલા શબ્દનો અર્થ ભૌમિતિક આકારને સતત ખેંચી, વાળીને નવો આકાર આપવાની પ્રક્રિયા થાય છે. વધારામાં, “if and only if " જેવા શબ્દસમૂહોનાં iiff જેવાં ટુંકાં શબ્દ સ્વરુપો ગણિતની પરિભાષામાં આવે છે. ખાસ સંકેતો અને શાસ્ત્રીય શબ્દભંડોળનું એક કારણ છે, તે એ કે ગણિતમાં રોજની બોલચાલની ભાષા કરતાં વધારે ચોક્સાઈની જરુર હોય છે.ગણિત વિદ્વાનો બને તેટલી સરળતા અને પારદર્શક્તાથી વસ્તુઓ પ્રસ્તુત કરવાનો પ્રયત્ન કરે છે અને ખાસ કરીને તે તેમના લખાણમાં આનો ખૂબ આગ્રહ રાખે છે. ભાષા અને તર્કની આ ચોક્સાઈને ગણિતશાસ્ત્રીઓ "ચોકસાઇનો અત્યાગ્રહ" કહે છે.

ગણિતીય સાબિતી મૂળભૂત રીતે ચોકસાઇના અત્યાગ્રહની વાત છે. પદ્ધતિસરની સમજ વડે, સ્વયંસિધ્ધ સત્યો પરથી જ પ્રમેયો આવવાં જોઈએ એમ ગણિતશાસ્ત્રી ઈચ્છે છે.તેનો હેતુ, ભૂલભરેલી અંતઃપ્રેરણા પર આધારિત, પ્રમેયોથી દૂર રહેવાનો છે, જેના દાખલા આ વિષયના ઈતિહાસમાં ઘણા બન્યા છે. ગણિતમાં અપેક્ષિત ચોકસાઇના અત્યાગ્રહની કક્ષામાં સમય સાથે ફેરફાર થાતા રહ્યા છે. ગ્રીકોની અપેક્ષા વિગતવાર દલીલોની હતી, પણ આઈઝેક ન્યૂટનના સમયમાં જે પધ્ધતિઓ વપરાતી તે ઓછી અત્યાગ્રહી હતી. ૧૯મી સદીમાં, ન્યુટને વાપરેલી વ્યાખ્યાઓમાંથી સહજ સમસ્યાઓ,કાળજીભર્યાં પ્રુથક્કરણ અને નિયમબધ્ધ સાબિતિઓનાં પુનરુત્થાન તરફ દોરી જવાની હતી.ગણિત વિષેના કેટલાક સામાન્ય ખોટા ખ્યાલો જ તેના ચોકસાઇના અત્યાગ્રહની વિષેની ગેરસમજ છે. આજે, કમ્પ્યુટરની મદદથી મળેલી સાબિતિઓ પર ગણિતશાસ્ત્રીઓમાં એકબીજા સાથે દલીલબાજી ચાલુ છે. બહુ મોટી ગણતરીઓને ચકાસી જોવાનું મુશ્કેલ હોવાથી, આવી સાબિતિઓની બાબતમાં ચોકસાઇનો પૂરતો આગ્રહ ન જળવાયો હોઇ શકે.

ચીલાચાલુ વિચાર પ્રમાણે ધારણાઓ એટલે "સ્વયંસિધ્ધ સત્યો",પણ એ ખ્યાલમાં સમસ્યા છે. નિયમ પ્રમાણે, સત્યો એ માત્ર ચિન્હોની શ્રુંખલા છે,જેનો એક સ્વયંસિધ્ધ સત્યોની પ્રણાલિનાં તારવી શકાય તેવાં બધાં સૂત્રોના સંદર્ભમાં જ માત્ર તાત્વિક અર્થ છે. હિલ્બર્ટના કાર્યક્રમનો હેતુ, સમગ્ર ગણિતશાસ્ત્રને સત્યોના એક ઠોસ પાયા પર મૂકવાનો હતો, પણ ગોડેલનાં "અપૂર્ણતાનાં પ્રમેય" પ્રમાણે , દરેક (પૂરતી શક્તિશાળી ) સત્ય પ્રણાલિમાં અનિશ્ચિત સૂત્રો હોય છે. તેથી ગણિતનું અંતિમ સ્વયંસિધ્ધ સત્યો પર આધારિત શાસ્ત્ર બનાવવું અશક્ય છે.એટલું જ નહીં, દરેક ગણિતીય વિધાન કે સાબિતિને ગણશાસ્ત્રનાં સૂત્રોમાં મૂકી શકાય તેમ માનવામાં આવે છે, એ રીતે ઘણીવાર ગણિતને (જ્યાં સુધી એના અભ્યાસક્રમની વાત છે), બીજું કંઈ નહીં પણ કેટલાંક સત્યો પર આધારિત ગણશાસ્ત્ર છે એમ માનવામાં આવે છે.

નાઇલ નદીના કિનારે અંદાજે ૨૦,૦૦૦ વર્ષ પુરાણી સંસ્કૃતિમાં ગણિત જાણીતું હોવાનુ મનાય છે. આ લોકોમાં સ્ત્રીઓ પોતાના માસિકની ગણત્રી માટે અમુક હાડકા પર કાપા કરીને ગણત્રી રાખતી. ત્યાર બાદની સંસ્કૃતિઓમાં ગણિતની મુખ્યત્વે જરૂરીયાત ખેતી, વ્યાપાર અને સૈન્યમાંથી આવી છે. સૌ પ્રથમ તો મનુષ્ય પશુને મારીને ખોરાક મેળવતો. પણ નદી કિનારે જે જે સંસ્કૃતિ વિકસી તે લોકો ખેતી અને પશુ દ્વારા પોતાનો ખોરાક મેળવતા. આ માટે તેમને ઋતુઓની ગણત્રી તેમજ જમીનની માપણી વિગેરેમાં ગણિતની જરૂર ઉભી થઇ. આમ પરોક્ષ રીતે ખગોળશાસ્ત્ર પણ ગણિતના જનક તરીકે ઓળખાય છે. ગણિતમાં માનવીના પ્રદાનના સૌથી જુના પ્રમાણિત પુરાવા આશરે ઇ.પૂ. ૩૦૦૦-૨૬૦૦ની ભારતમાં વિકસેલી હરપ્પા સંસ્કૃતિ તેમજ મિસોપોટામિયા/બેબીલોન (આજના ઇરાકની આજુ બાજુનો ભાગ)માં વિકસેલી સુમેર સંસ્કૃતિ ઇ.પૂ. ૨૬૦૦ તેમજ આશરે ઇ.પૂ. ૨૭૦૦-૧૩૦૦માં વિકસેલી ઇજીપ્તની સંસ્કૃતિમાં જોવા મળે છે. એરિક ટેમ્પલ બેલ જેવા ગણિતના ઇતિહાસકારોના મતે ગણિત તેની બે મુખ્ય શાખાઓ -- સંખ્યા અને આકાર--માંથી વિક્સ્યુ છે. કાળક્રમે સંખ્યામાંથી બીજ ગણિત અને આકારમાંથી ભૂમિતિનો જન્મ થયો.

માળખાંઓના અભ્યાસની શરૂઆત સંખ્યાઓથી થાય છે, જેમાં સૌ પ્રથમ પ્રાકૃતિક સંખ્યાઓ ત્યાર બાદ પૂર્ણાંકો અને તેમની દ્વિકક્રિયાઓ આવે છે. પૂર્ણાંકોનો વધુ ગહન અભ્યાસ નંબર થીયરી અહીંથી આગળ વધતાં સમીકરણોના ઉકેલ મેળવવાની પ્રક્રિયામાંથી બીજ ગણિત અને અમૂર્ત ગણિતનો વિકાસ થયો. આમાં મુખ્યત્વે સમુહ (groups), મંડળ (rings), ક્ષેત્ર (Fields) ઇત્યાદિનો સમાવેશ થાય છે. આ શાખાના ની ઉપશાખા ગાલ્વા થીયરીના કારણે ગ્રીક કાળથી વણઉક્લ્યો કંપાસની મદદથી રચના કરવાને લગતો જાણીતો પ્રશ્ન હલ થયો. ભૌતિકવિજ્ઞાનના સદિશ (vector)ના અભ્યાસનું વ્યાપકીકરણ (generalization) કરી સદિશાવકાશની શોધ કરી. આમ સુરેખ ગણિત (Linear Algebra)નું અસ્તિત્વ ઉભું થયું જે માળખું અને અવકાશ બન્નેમાં આવે છે. સુરેખ ગણિત અને સદિશાવકાશની સાથે વખત જતાં ટોપોલોજી જોડતાં વીસમી સદીમાં ગણિતના મોરની કલગીની જેમ ફંક્શનલ એનાલિસીસનો જન્મ અને વિકાસ થયો.

અવકાશના અભ્યાસની શરૂઆત ભૂમિતિથી થઇ. સૌ પ્રથમ આવી તે ભૂમિતિ યુક્લિડીયન ભૂમિતિના નામે ઓળખાય છે. હકીકતે ભૂમિતિ ભારતીયો, બેબીલોનિયનો તેમજ ઇજીપ્શીયનો જાણતા હતા પણ યુક્લિડે તેના અભ્યાસને સૌ પ્રથમ પૂર્વધારણાઓ અને તેના પરથી પરીણામોના ફલનની રીતે (deductive reasoning) વ્યવસ્થિત ઢાંચામાં મુક્યો. ગણિતજ્ઞોની મતે યુક્લિડે આપેલી બે સોગાદો -ભૂમિતિનું સંપાદન અને ડીડક્ટીવ રીઝનીંગ - પૈકી ડીડક્ટીવ રીઝનીંગની ભેટ સૌથી મહત્વની છે. અવકાશના અભ્યાસ દરમ્યાન સ્વતંત્ર રીતે ત્રિકોણમિતિ વિધેયોનો અભ્યાસ પણ વિકસ્યો. ત્રિકોણમિતિનો ઊંડો અભ્યાસ હિન્દુ ગણિતમાં જોવા મળે છે. યજ્ઞવેદી, તેમજ વાસ્તુશાસ્ત્ર પ્રમાણેના ધાર્મિક સ્થાપત્યો બનાવવા માટે ત્રિકોણમિતિનો આવિષ્કાર હિન્દુઓ દ્વારા થયો હોવાનું ગણિતના ઇતિહાસકારો માને છે. સલ્બસુત્ર તેમજ સ્થાપત્ય વેદમાં આ પ્રકારના ગણિત જોવા મળે છે. ભૂમિતિના નવા આયામો માં ડિફરન્શિયલ ભૂમિતિ, એલ્જીબ્રીક ભૂમિતિ, નોનયક્લિડીય ભૂમિતિઓ, તેમજ એકદમ અરૂપ રીતે ટોપોલોજીનો સમાવેશ થાય છે.

ગણિતમાં ફેરફારના દરને કારણે જે ગણિતનો આવિષ્કાર થયો તે કેલ્કયુલસ શોધ ન્યૂટન તેમજ લાઇબ્નીઝના ફાળે જાય છે. કહેવાય છે કે ઇ.પૂ. ૨૮૭માં ગ્રીક ગણિતજ્ઞ આર્કિમીડિઝ પોતાના વખત કરતાં એટલો આગળ હતો કે તેણે કેલ્ક્યુલસના ઘણા પરીણામો તેના અભ્યાસમાં વાપર્યા હતાં. ન્યુટન માટે તેમ કહેવાય છે કે તેણે પોતાના જન્મ પહેલાં શોધાયેલા તમામ ગણિતના જ્ઞાન જેટલું નવું ગણિત રચ્યું હતું. કેલ્ક્યુલસ ના કારણે ગણિતના વિકાસનો દર ખૂબ જ વધી ગયો અને તે અન્ય વિજ્ઞાનોમાં પણ ખૂબજ વપરાવા લાગ્યું. હાલ ગણિતની લગભગ ૧૦૦૦ ઉપરાંત મુખ્ય શાખાઓ છે. કેલ્ક્યલસનો સૌથી પાયાની સંકલ્પના એટલે ચલ રાશિ અને વિધેય જે આજે ગણિતની તમામ શાખાઓમાં વપરાય છે. આ ચલ રાશિને અનુલક્ષીને વધુ અમૂર્ત સંકલ્પના એટલે ગણ. ગણ સિદ્ધાંતનો આવિષ્કાર ૧૮૭૦ની આસપાસ ડેડકિન્ડ તેમજ કેન્ટર નામના ગણિતજ્ઞોએ તેના ઔપચારિક ખ્યાલોને વ્યાખ્યાયિત કરીને કર્યો. ગણિતની પાયાની વધુ શાખાઓમાં વિકલીય સમીકરણો, સંકલીય સમીકરણો, વાસ્તવિક સંખ્યાઓ, સંકર સંખ્યાઓ, તેમજ તર્કશાસ્ત્ર વિગેરેનો સમાવેશ થાય છે.

 

વિશાળ અર્થમાં ગણિતશાસ્ત્રના ભાગલા આ રીતે પાડી શકાય : જથ્થાનો અભ્યાસ, માળખાંનો અભ્યાસ, અવકાશનો અભ્યાસ અને બદલાવનો અભ્યાસ. (એટલે કે અંકગણિત, બીજગણિત, ભૂમિતિ અને પ્રુથક્કરણ.) આ મુખ્ય હેતુઓ ઉપરાંત ગણિતના હાર્દમાંથી બીજાં ક્ષેત્રો જેવાં કે તર્કશાસ્ત્ર, ગણશાસ્ત્રનો પાયો, જુદાં જુદાં વિજ્ઞાનનાં પ્રયોગમૂલક ગણિત (પ્રયોજિત ગણિત) અને વધારે અદ્યતન, અચોક્કસતાના અભ્યાસ સાથે જોડતા સંબંધો શોધવા માટે સમર્પિત વિભાગો છે.

પાયો અને તત્વજ્ઞાન.

ગણિતના પાયાને સ્પષ્ટ કરવા માટે, ગણિતીય તર્કશાસ્ત્ર અને ગણશાસ્ત્રનાં ક્ષેત્રોનો વિકાસ થયો.ગણિતીય તર્કશાસ્ત્રમાં તર્કશાસ્ત્રનો ગણિતની દૃષ્ટિએ અભ્યાસ અને તેનો ગણિતના બીજા વિભાગોમાં ઉપયોગોની સમજ આવે છે.વસ્તુઓના સમૂહનો અભ્યાસ ગણિતની જે શાખામાં કરવામાં આવે છે તે ગણશાસ્ત્ર છે. ગણિતીય માળખાં અને તેની વચ્ચેના સંબંધોનો અમૂર્ત રીતે અભ્યાસ કરતી કેટેગરી થિયરી હજી વિકાસના તબક્કામાં છે. આશરે ઈ.સ. ૧૯૦૦થી ઈ.સ. ૧૯૩૦ સુધી ગણિતશાસ્ત્રના પાયાની ચોકસાઇની અત્યાગ્રહી શોધ ચાલી. તેને "પાયાની કટોકટી" એ શબ્દોમાં વર્ણવવામાં આવે છે. આજ સુધી પણ ગણિતના પાયા વિષે કેટલાક મતભેદ પ્રવર્તે છે. એ સમયે પ્રચલિત, કેંટરનાં ગણશાસ્ત્ર પરનો વાદવિવાદ અને બ્રૌવેર- હિલ્બર્ટ વાદવિવાદ જેવા ઘણા વાદવિવાદોએ પાયાની કટોકટીને ઉત્તેજી.

ગણિતીય તર્કશાસ્ત્રનું કામ, ગણિતને અત્યાગ્રહી ચોક્સાઇનાં સૈધ્ધાંતિક માળખાંમાં મૂકવાનું અને એવાં માળખાંના સૂચિતાર્થનો અભ્યાસ કરવાનું છે. આ રીતે તેમાં ગોડેલનું પ્રમેય છે જે (અનઔપચારીકપણે) જણાવે છે કે મૂળભૂત અંકગણિત આવરી લેતી હોય તેવી કોઈ પણ પ્રભાવશાળી નિયમોની પ્રણાલિ, જો મજબૂત હોય (એટલે કે જેમાં સાબિત થઈ શકે તેવાં બધાં પ્રમેયો સત્ય છે) તો તે અનિવાર્યપણે અપૂર્ણ છે. (એટલે કે તેમાં સાચાં પ્રમેયો પણ છે જેને એ પ્રણાલિમાં સાબિત કરી શકાતાં નથી.) પાયા તરીકે સંખ્યાશાસ્ત્રને લગતા સિધ્ધાંતોનો કોઈ પણ ચોક્કસ સમૂહ લઈએ, ગોડેલએ બતાવ્યું કે સંખ્યાશાસ્ત્રની સાચી સૈદ્ધાંતિક હકીકત રજૂ કરે એવું નિયમ વિધાન કેવી રીતે બનાવવું , જે આ સિધ્ધાન્તો પરથી પ્રતિપાદિત થતું નથી. તેથી સંપૂર્ણ સંખ્યાશાસ્ત્રની પૂરેપૂરી સૈધ્ધાંતિકરણ હોય તેવી કોઇ નિયમ પ્રણાલિ નથી.આધુનિક તર્કશાસ્ત્ર, રિકર્ઝન થિયરી, મોડેલ થિયરી અને પ્રુફ થિયરીમાં વિભાજિત થયેલું છે અને શાસ્ત્રીય કમ્પ્યુટર વિજ્ઞાન [citation needed] અને કેટેગરી થિયરી સાથે બહુ નજીકથી સંકળાયેલું છે. શાસ્ત્રીય કમ્પ્યુટર વિજ્ઞાનમાં ગણતરીપાત્રતાનું શાસ્ત્ર, ગણતરીને લગતી આંટીઘૂંટીનું શાસ્ત્ર અને માહિતીનું શાસ્ત્ર આવે છે.ગણતરીપાત્રતાનું શાસ્ત્ર, કમ્પ્યુટરના જુદા જુદા શાસ્ત્રીય નમૂનાઓની મર્યાદાની કસોટી કરે છે, જેનો પ્રખ્યાત નમૂનો the Turing machine છે.

ગણતરીને લગતી આંટીઘૂંટીનું શાસ્ત્ર એ, કમ્પ્યુટર વડે તેની કાબુમાં રાખી શકવાની શક્તિનો અભ્યાસ છે. કેટલીક સમસ્યાઓ, સૈધ્ધાંતિક રીતે કમ્પ્યુટરથી ઉકેલી શકાય તેવી હોય તો પણ સમય અને જગ્યાની બાબતમાં એટલી ખર્ચાળ હોય કે તેનો ઉકેલ વ્યાવહારિક રીતે અશક્ય જ રહેવાનો. કમ્પ્યુટર હાર્ડવેરના ઝડપી આધુનિકરણ છતાં પણ હજૂ આ પરિસ્થિતિ છે. આવો એક બહુ પ્રખ્યાત કોયડો, " P = NP? " છે, જે મિલેનિયમ ઈનામી કોયડામાંનો એક છે. અને છેલ્લે, માહિતીશાસ્ત્રને આપેલાં માધ્યમમાં સંઘરી શકાય એવા માહિતીના જથ્થા સાથે સંબંધ છે.તેથી જ એ સંક્ષેપ (Compression) અને ઉત્ક્રમ (Entropy) જેવા મૂળભૂત ખ્યાલો ઉપર કામ કરે છે.

${\displaystyle p\Rightarrow q\,}$
ગણિતીય તર્કશાસ્ત્ર	ગણશાસ્ત્ર	Category theory	Theory of computation

શુધ્ધ ગણિતશાસ્ત્ર :

જથ્થો

જથ્થાનો અભ્યાસ સંખ્યાઓથી શરુ થાય છે.પ્રથમ આવે છે પ્રાકૃતિક સંખ્યાઓ અને પૂર્ણાંકો (પૂર્ણ સંખ્યાઓ ) અને અંકગણિતે આલેખેલી તે સંખ્યાઓ પરની ક્રિયાઓ. સંખ્યાશાસ્ત્રમાં પૂર્ણાકોના ઊંડાણભર્યા ગુણધર્મોનો અભ્યાસ કરવામાં આવે છે.એ પરથી "ફરમાનું છેલ્લું પ્રમેય" જેવાં લોકપ્રિય પરિણામો મળ્યાં છે. જોડિયાં અવિભાજ્ય સંખ્યાઓનું અનુમાન (The twin prime conjecture ) અને ગોલ્ડબાકનું અનુમાન (Goldbach's conjecture) એ સંખાશાસ્ત્રના બે વણઉકેલાયેલા કોયડા છે.

જેમ જેમ સંખ્યાપ્રણાલિનો આગળ વિકાસ થયો તેમ પૂર્ણાંકોને સંમેય સંખ્યાઓ (અપૂર્ણાંકો)ના ઉપગણ તરીકે ઓળખાવાયા. આ બધી સંખ્યાઓ પાછી વાસ્તવિક સંખ્યાઓના સમૂહમાં સમાવી લેવામાં આવી છે. એ સંખ્યાઓનો, જથ્થાને અસ્ખલિત રુપે દર્શાવવા માટે ઉપયોગ થાય છે.વાસ્તવિક સંખ્યાઓનું સામાન્યીકરણ સંકુલ સંખ્યાઓમાં થાય છે. સંખ્યાઓના અધિક્રમમાં આ પ્રથમ પગથિયાં છે કે જેમાં આગળ જતાં ૪ સંખ્યાસમૂહ quaternions અને octonions નો સમાવેશ થાય છે.પ્રાકૃતિક સંખ્યાઓને ધ્યાનમાં લેતાં આપણે અગણિત સંખ્યાઓ(transfinite numbers) મળે છે.જેના પરથી "અનંત" નો ખ્યાલ બાંધી શકાયો છે.અભ્યાસનો બીજો વિભાગ કદને લગતો છે. તેના પરથી કાર્ડિનલ સંખ્યાઓ અને અનંતનો એક બીજો ખ્યાલ, એલેફ સંખ્યાઓ મળે છે, એના લીધે અનંત રીતે મોટા ગણનાં કદની અર્થપૂર્ણ સરખામણી થઈ શકે છે.

${\displaystyle 1,2,\ldots }$	${\displaystyle 0,1,-1,\ldots }$	${\displaystyle {\frac {1}{2}},{\frac {2}{3}},0.125,\ldots }$	${\displaystyle \pi ,e,{\sqrt {2}},\ldots }$	${\displaystyle i,3i+2,e^{i\pi /3},\ldots }$
પ્રાકૃતિક સંખ્યાઓ	પુર્ણાંક સંખ્યાઓ	અપુર્ણાંક સંખ્યાઓ	વાસ્તવિક સંખ્યાઓ	સંકર સંખ્યાઓ

સંખ્યાઓ – પ્રાકૃતિક સંખ્યાઓ – પુર્ણાંક સંખ્યાઓ – અપુર્ણાંક સંખ્યાઓ – વાસ્તવિક સંખ્યાઓ – સંકર સંખ્યાઓ – Hypercomplex number – Quaternion – Octonion – Sedenion – Hyperreal number – Surreal number – Ordinal number – Cardinal number – p-adic numbers – Integer sequences – ગાણિતીક અચળાંક – Number names – Infinity – Base

માળખુ

સંખ્યાઓ અને વિધેયોના ગણ જેવી ઘણી ગણિતીય વસ્તુઓ, એ ગણ પર વ્યાખ્યાયિત કરેલી ક્રિયાઓ અને સંબંધોના પરિણામ સ્વરુપે, આંતરિક માળખું બતાવે છે.એ પછી એ માળખાંના સંદર્ભમાં વ્યક્ત કરી શકાય તેવા ગણના ગુણધર્મોનો ગણિત અભ્યાસ કરે છે.દા. ત. અંકગણિતની ક્રિયાઓમાં વ્યક્ત કરી શકાય તેવા પૂર્ણાંકોના ગણના ગુણધર્મોનો અભ્યાસ સંખ્યાશાસ્ત્ર કરે છે.એ ઉપરાંત, ઘણીવાર એવું બને છે કે આવા વિવિધ માળખાંરુપ ગણો, સરખા જ ગુણધર્મો બતાવે છે.જેને કારણે, અમૂર્તતાનું એક પગલું આગળ ભરીને, માળખાંઓના મોટા વર્ગ માટે સ્વયંસિદ્ધ સિધ્ધાંતો કહેવા અને પછી આ સ્વયંસિદ્ધ સિધ્ધાંતોને અનુરુપ આખા વર્ગનાં માળખાંઓનો અભ્યાસ કરવો એ શક્ય બને છે.આવી રીતે કોઈ પણ ગ્રુપ, રીંગ અને ફિલ્ડ અને બીજી તાત્વિક પ્રણાલિઓનો અભ્યાસ કરી શકાય છે.આવા અભ્યાસ ( બિજગણિતીય ક્રિયાઓ વડે વ્યાખ્યાયિત થયેલાં માળખાં માટે) તાત્વિક બીજગણિતનું કાર્યક્ષેત્ર રચે છે.તાત્વિક બીજગણિત, તેની બહુ મોટી સામાન્યતાને લીધે, દેખીતી રીતે એક બીજાથી સંબંધ ન ધરાવતી સમસ્યાઓ માટે પણ પ્રયોજી શકાય છે. દા. ત. કમ્પાસ અને ફૂટપટ્ટીથી થતી રચનાઓ સંબંધી ઘણા પ્રાચીન કોયડાઓના ઉકેલ છેવટે ગેલીઓસ થિયરીથી થયા, જેમાં ફિલ્ડ થિયરી અને ગ્રુપ થિયરી આવે છે.બીજગણિતીય શાસ્ત્રનો બીજો દાખલો સુરેખ બીજગણિત છે, જેમાં વેક્ટર અવકાશનો સામાન્ય અભ્યાસ થાય છે."વેક્ટર અવકાશ" ગણના ઘટકો વેક્ટર છે જેને માપ અને દિશા બન્ને છે.તેનો ઉપયોગ, અવકાશનાં બિંદુઓ અને તેની વચ્ચેના સંબંધો દર્શાવવા થાય છે.આ એવી ઘટનાનો એક દાખલો છે કે મૂળભૂત રીતે એકબીજાં સાથે કંઈ સંબંધ ન હોય તેવા બીજગણિત અને ભૂમિતિનાં ક્ષેત્રો વચ્ચે આધુનિક ગણિતશાસ્ત્રમાં મજબૂત આદાનપ્રદાન થાય છે. આપેલાં માળખાંમાં , કેટલી સંખ્યામાં ખૂબ વસ્તુઓને સમાવી શકાય તે જાણવાની રીતોનો અભ્યાસ કોમ્બિનેટોરિક્સમાં કરવામાં આવે છે.

${\displaystyle {\begin{matrix}(1,2,3)&(1,3,2)\\(2,1,3)&(2,3,1)\\(3,1,2)&(3,2,1)\end{matrix}}}$
કોમ્બિનેટોરિક્સ	સંખ્યાશાસ્ત્ર	Group theory	Graph theory	Order theory	બીજગણિત

નિમ્નલિખિત વિષયો ગણિત નો વિસ્તાર,સમમિતિ અને માળખુ દર્શાવે છે.

સંક્ષિપ્ત બીજગણિત – સંખ્યઓનો સિધ્ધાંત – બીજગાણિતિક ભૂમિતી – ગ્રુપ થિયરી – Monoids – વિશ્લેષણ – સંસ્થિતિ શાસ્ત્ર – રેખિત બીજગણિત – ગ્રાફ થિયરી – સાર્વત્રિક બીજગણિત – કેટેગરી થિયરી – ઓર્ડર થિયરી – માપન થિયરી

અવકાશ

અવકાશના અભ્યાસનું મૂળ ભૂમિતિમાં છે, ખાસ કરીને યુક્લિડની ભૂમિતિમાં. ત્રિકોણમિતિ ગણિતની એવી શાખા છે, જે ત્રિકોણની બાજુઓ અને ખૂણા વચ્ચેના સંબંધોનો અને ત્રિકોણમિતીય વિધેયોનો અભ્યાસ કરે છે.એ અવકાશ અને સંખ્યાઓને સાંકળે છે. અને બહુ જાણીતાં પાયથાગોરસ પ્રમેયને આવરી લે છે. અવકાશનો આધુનિક અભ્યાસ, આ વિચારોને સામાન્ય બનાવીને, તેમાં બહુ પરિમાણવાળી ભૂમિતિ, યુક્લિડ સિવાયની ભૂમિતિઓ (જે સામાન્ય સાપેક્ષતામાં કેન્દ્રનો ભાગ ભજવે છે) અને ટોપોલોજીને સમાવી લે છે. પ્રુથક્કરણીય ભૂમિતિ, વિકલન આધારિત ભૂમિતિ અને બીજગણિત આધારિત ભૂમિતિ એ બધા વિષયમાં, જથ્થો અને અવકાશ બન્ને ભાગ ભજવે છે. બહિર્ગોળ (Convex) અને સુસ્પષ્ટ(Discrete) ભૂમિતિનો વિકાસ,સંખ્યાશાસ્ત્ર અને વિધેયોના પ્રુથક્કરણને લગતાં શાસ્ત્રના કોયડા ઉકેલવા માટે થયો.આજે હવે તેનો અભ્યાસ યથોચિતકરણ (Optimization) અને કમ્પ્યુટર વિજ્ઞાનમાં પ્રયોજવા માટે થઈ રહ્યો છે.વિકલ ભૂમિતિમાં તંતુઓના સમૂહના અને કલનશાસ્ત્રના વિવિધ , ખાસ કરીને વેક્ટર અને ટેન્સર કલનશાસ્ત્રના ખ્યાલો રહેલા છે.બીજગણિતીય ભુમિતિમાં બહુપદી સમીકરણોના ઉકેલના સમૂહ તરીકે, ભૌમિતિક વસ્તુઓનું વર્ણન રહેલું છે, જે જથ્થા અને અવકાશના ખ્યાલોને ભેગા કરે છે.તેમાં ટોપોલોજીના સમૂહોનો પણ અભ્યાસ છે જેમાં માળખાંને અને અવકાશને એકત્ર કરવામાં આવે છે. લાય સમૂહોનો ઉપયોગ અવકાશ, માળખાં અને બદલાવના અભ્યાસ માટે થાય છે.વીસમી સદીનાં ગણિતશાસ્ત્રમાં, અનેક શાખા-પ્રશાખામાં વિભાજિત થઈને ટોપોલોજીનો વિષય સૌથી વધારે વિકસતું ક્ષેત્ર હોઈ શકે છે. તેનાં ક્ષેત્રમાં બિંદુગણ ટોપોલોજી, ગણશાસ્ત્રીય ટોપોલોજી, બિજગણિતીય ટોપોલોજી અને વિકલન ટોપોલોજી આવરી લેવાયાં છે. આધુનિક ટોપોલોજીનાં ઉદાહરણોમાં મેટ્રીઝેબીલીટી થિયરી, એક્ષિઓમૅટિક સૅટ થિયરી, હોમોટોપી થિયરી અને મોર્સ થિયરી મુખ્ય છે. ટોપોલોજીમાં હવે ઉકેલાઇ ચૂકેલ પૉઇનકૅરૅ અનુમાન અને હૉજ અનુમાનનાં વણઉકેલાયેલાં ક્ષેત્રો પણ આવરી લેવાયેલ છે. ભૂમિતિ અને ટોપોલોજીનાં ચાર રંગનું પ્રમેય અને કેપ્લર અનુમાન જેવાં પરિણામો તો કમ્પ્યુટરની મદદથી જ ઉકેલી શકાયાં છે.

ક્ષેત્રવિદ્યા	ભૂમિતિ	ત્રિકોણમિતિ	વિકલનીય ભૂમિતિ	Fractal geometry

ક્ષેત્રવિદ્યા – ભૂમિતિ – ત્રિકોણમિતિ – બીજગણિતીય ભૂમિતિ – વિકલનીય ભૂમિતિ – વિકલનીય ક્ષેત્રવિદ્યા – બીજગણિતીય ક્ષેત્રવિદ્યા – રેખીય બીજગણિત – અપૂર્ણાંક ભૂમિતિ

પરિવર્તન

ગાણિતિક વિધેયના અને સંખ્યાઓના પરિવર્તનને વ્યક્ત કરવાની પધ્ધતીઓ.

બધાં જ કુદરતી વિજ્ઞાનનો એક સામાન્ય વિષય છે બદલાવને સમજવો અને વર્ણવવો. આ સમજવા માટેનાં એક શક્તિશાળી સાધન તરીકે કલનશાસ્ત્રનો વિકાસ થયો.બદલતા જથ્થાને વર્ણવવા માટેના કેન્દ્રવર્તી ખ્યાલ તરીકે અહીં વિધેયો બને છે.વાસ્તવિક સંખ્યાઓના અને વાસ્તવિક ચલ સંખ્યાઓના વિધેયોનો ઊંડાણભર્યા અભ્યાસ વાસ્તવિક પ્રુથક્કરણશાસ્ત્ર તરીકે ઓળખાય છે.સંકુલ સંખ્યાઓના એવા જ ક્ષેત્રને સંકુલ પ્રુથક્કરણશાસ્ત્ર કહેવામાં આવે છે. વિધેયાત્મક પ્રુથક્કરણશાસ્ત્રમાં (ખાસ અગણિત પરિમાણવાળા) વિધેયના અવકાશ પર ધ્યાન કેન્દ્રિત કરવામાં આવે છે.વિધેયાત્મક પ્રથક્કરણશાસ્ત્રના ઘણા ઉપયોગોમાંનો એકછે ક્વોન્ટમ મિકેનિક્સ. ઘણા કોયડાઓ, જથ્થો અને તેના બદલાવના દર વચ્ચેના સંબંધો તરફ લઈ જાય છે, જેનો અભ્યાસ વિકલ સમીકરણો તરીકે કરવામાં આવે છે.કુદરતની ગણી ઘટનાઓનું વર્ણન ગતિશાસ્ત્રની પ્રણાલિઓ વડે થઈ શકે છે. કેઓસ થિયરી (ગેરવ્યવસ્થાશાસ્ત્ર) ચોક્કસ રીતો બનાવે છે જેમાં આમાંની ઘણી પ્રણાલિઓ અણધાર્યું અને છ્તાં નિશ્ચિત કરી શકાય એવું વર્તન બતાવે છે.

${\displaystyle 36\div 9=4}$			${\displaystyle \int 1_{S}\,d\mu =\mu (S)}$
અંક ગણિત	કલન શાસ્ત્ર	સદિશ કલન શાસ્ત્ર	ગાણિતિક વિશ્લેષણ
${\displaystyle {\frac {d^{2}}{dx^{2}}}y={\frac {d}{dx}}y+c}$
વિકલ સમીકરણ	ગતિમય તંત્ર	અવ્યવસ્થા(કેઓસ્)નો સિધ્ધાંત્

અંક ગણિત્ – કલન શાસ્ત્ર – સદિશ કલનશાસ્ત્ર્ – ગાણિતિક વિશ્લેષ્ણ્ – વિકલ સમીકરણ – ગતિમય તંત્ર – અવ્યવસ્થાનો સિધ્ધાંત – વિધેયો ની યાદી

Discrete mathematics

Discrete mathematics involves techniques that apply to objects that can only take on specific, separated values.

Naive set theory	Theory of computation	Cryptography	Graph theory

Combinatorics – Naive set theory – Theory of computation– Cryptography – Graph theory

પ્રયોજિત ગણિતશાસ્ત્ર

પ્રયોજિત ગણિતશાસ્ત્ર, ગણિતની એ પધ્ધતિઓ સાથે સંબંધ ધરાવે છે જે ખાસ તો વિજ્ઞાન,તંત્રવિદ્યા, વ્યાપારધંધા અને ઉદ્યોગોમાં વપરાય છે. આમ, " પ્રયોજિત ગણિતશાસ્ત્ર " એ ખાસ જાતનું જ્ઞાન ધરાવતું, ગણિતીય વિજ્ઞાન છે. પ્રયોજિત ગણિતશાસ્ત્ર એ શબ્દો, વ્યાવસાયિક ખાસિયતોને પણ વર્ણવે છે.એમાં ગણિતશાસ્ત્રીઓ વ્યવહારિક સમસ્યાઓ પર કામ કરે છે.વ્યાવહારિક કોયડાઓ પર કેન્દ્રિત વ્યવસાય તરીકે, પ્રયોજિત ગણિતશાસ્ત્ર વિજ્ઞાન, તંત્રવિદ્યા, અને ગણિતીય વ્યવહારનાં બીજાં ક્ષેત્રોમાં "ગણિતિય નમૂનાઓની રચના,અભ્યાસ અને ઉપયોગો" પર ભાર મૂકે છે.

ભૂતકાળમાં વ્યાવહારિક ઉપયોગોએ ગણિતીય સિધ્ધાંતોના વિકાસને ઉત્તેજ્યો, જે પછીથી શુધ્ધ ગણિતશાસ્ત્રના અભાસનો વિષય બન્યો કે જેમાં ગણિતનો અભ્યાસ તેના પોતાના ખાતર જ કરવામાં આવે છે. આમ પ્રયોજિત ગણિતશાસ્ત્રની પ્રવૃતિ, શુધ્ધ ગણિતશાસ્ત્રનાં શોધકાર્ય સાથે અગત્યપણે સંકળાયેલી છે.

આંકડાશાસ્ત્ર અને બીજાં નિર્ણયાત્મક વિજ્ઞાન

પ્રયોજિત ગણિતશાસ્ત્ર, આંકડાશાસ્ત્રની સાથે મહત્ત્વનું આચ્છાદન ધરાવે છે. તેના સિધ્ધાંતો, ખાસ કરીને સંભાવનાશાસ્ત્ર,ની રચના ગણિતીય રીતે થયેલી છે. (શોધકાર્ય પ્રકલ્પના એક ભાગ તરીકે કામ કરતાં) આંકડાશાસ્ત્રીઓ, યાર્દચ્છીક નમૂનાઓ લેવાની ક્રિયા વડે અને યાર્દચ્છીક પ્રયોગોથી, "યથાર્થ માહિતી ઊભી કરે છે." અને (માહિતી મળ્યા પહેલાં જ) આંકડાકીય નમૂના અથવા પ્રયોગની રચના માહિતીનાં પ્રુથક્કરણને સુનિશ્ચિત કરે છે.આંકડાશાસ્ત્રીઓ જ્યારે પ્રયોગો અને નમૂનાઓ પરથી માહિતીને ફરીથી હાથ પર લે છે અથવા જ્યારે નિરિક્ષણ આધારિત અભ્યાસ પરથી માહિતીનુ અર્થપૂર્ણ પૃથક્કરણ કરે છે ત્યારે, નમૂના લેવાની કળા અને નિષ્કર્ષ સિધ્ધાંતનો ઉપયોગ કરીને, નમૂનાની પસંદગી અને આકારણીથી, "માહિતીને વધારે યથાર્થ બનાવે છે." આકારિત નમૂનાઓ અને પરિણામસ્વરુપ આગાહીઓ ની કસોટી નવી માહિતી પર કરવી જોઈએ.

આંકડાકીય સિધ્ધાંતો, આંકડાકીય કાર્યનાં જોખમ (અપેક્ષિત નુકસાન) ને ઓછું કરવું, જેવાં કે પ્રાચલની આકારણી, પૂર્વધારણાની કસોટી અને શ્રેષ્ઠની પસંદગી માટે એક પધ્ધતિનો ઉપયોગ કરવો જેવી નિર્ણય સમસ્યાઓનો અભ્યાસ કરે છે. ગણિતીય આંકડાશાસ્ત્રના આ રુઢિગત ક્ષેત્રોમાં , ખાસ અવરોધોની હાજરીમાં, અપેક્ષિત ખર્ચ કે નુકસાન જેવાં હેતુગત વિધેયોમાં ઘટાડો કરીને, એક આંકડાકીય નિર્ણય-સમસ્યાની રચના કરવામાં આવે છે. દા. ત. મોજણીની રચનામાં, વિશ્વાસપાત્રતાની એક આપેલી સપાટી સાથે, સમગ્ર માહિતિની આકારણી કરવાનો ખર્ચ ઓછામાં ઓછો કરવાની વાત આવે છે. ગણિતીય આંકડાશાસ્ત્ર, તેના યથોચિતપણાંના ઉપયોગને કારણે ઓપરેશન્સ રિસર્ચ, કન્ટ્રોલ થિયરી અને ગણિતીય અર્થશાસ્ત્ર જેવા બીજાં નિર્ણયલક્ષી વિજ્ઞાન સાથે સંબંધ ધરાવે છે. ]

કમ્પ્યુટરલક્ષી ગણિતશાસ્ત્ર

માનવસહજ સંખ્યાકીય ક્ષમતા માટે અતિ મોટા પડે તેવા ખાસ ગણિતીય કોયડાઓને ઉકેલવા માટેની પધ્ધતિઓનું સૂચન અને અભ્યાસ જેમા થાય છે તે કમ્પ્યુટરલક્ષી ગણિતશાસ્ત્ર છે. વિધેયલક્ષી પ્રુથક્કરણ અને અંદાજીકરણના સિધ્ધાંતોનો ઉપયોગ કરીને,પ્રુથક્કરણના કોયડાઓ માટેની પધ્ધતિનો અભ્યાસ સંખ્યાકીય પ્રુથક્કરણમાં થાય છે.સંખ્યાકીય પ્રુથક્કરણમાં અંદાજીકરણ અને અલગીકરણનો મોટે ભાગે અભ્યાસ થાય છે. તેનો ખસ સંબંધ ભૂલોને હળવી બનાવવાનો છે.સંખ્યાકીય પ્રુથક્કરણ અને વધારે આગળ વૈજ્ઞાનિક ગણતરીશાસ્ત્ર, પ્રુથક્કરણલક્ષી ન હોય તેવા ગણિતીય વિજ્ઞાનના વિષયો, ખાસ કરીને અલ્ગોરિધમ શ્રેણિક અને આલેખશાસ્ત્રનો અભ્યાસ છે.કમ્પ્યુટરલક્ષી ગણિતશાસ્ત્રનાં બીજાં ક્ષેત્રોમાં કમ્પ્યુટર બીજગણિત અને સાંકેતિક ગણતરીના વિષયો આવે છે.

Applied mathematics uses the full knowledge of mathematics to solve real-world problems.

Mechanics – Numerical analysis – Optimization – Probability – Statistics – Financial mathematics – Game theory – Mathematical biology – Cryptography – Information theory – Fluid dynamics

ગણિતનાં પારિતોષિક/ખિતાબો (awards) સામાન્યતઃ વિજ્ઞાનથી અળગા હોય છે. ગણિતનો સૌથી વધુ મહત્તા ધરાવતું પારિતોષિક ફિલ્ડ મેડલ, ૧૯૩૬માં સ્થાપવામાં આવ્યું હતું અને હવે દર ચાર વર્ષે ૪૦ વર્ષથી નીચેના કોઈક ગણિતજ્ઞને એનાયત થાય છે. તેને ગણિતના નોબલ પુરસ્કાર તરીકે ઓળખવામાં આવે છે. ૧૯૭૮માં સ્થપાયેલું વુલ્ફ પારિતોષિક ગણિતશાસ્ત્રીઓના જીવનકાળ દરમ્યાનમાં તેમના યોગદાન માટે એનાયત કરવામાં આવે છે. આ સિવાય બીજા નામના ધરાવતા પારિતોષિકમાં અબેલ પારિતોષિક (સ્થાપના ૨૦૦૩) છે. આ પારિતોષિક ગણિતના ઘણા સમયથી વલઉક્લ્યા પ્રશ્નોના ઉકેલ મેળવનારને અપાય છે. આવા જ ૨૩ વણઉકલ્યા પ્રશ્નોની યાદી જર્મન ગણિતજ્ઞ ડેવિડ હિલ્બર્ટે ૧૯૦૦માં સંપાદિત કરી હતી જે "હિલ્બર્ટના પ્રશ્નો" તરીકે ખૂબજ પ્રખ્યાત છે. આ યાદીના લગભગ ૯ જેટલા પ્રશ્નો અત્યાર સુધીમાં ઉકેલી શકાયા છે. આ સિવાય "w:en:Millennium Prize Problems" તરીકે જાણીતી યાદીનું સંપાદન સન ૨૦૦૦માં કરવામાં આવ્યું હતું. આ પૈકીના કોઇપણ પ્રશ્નનો ઉકેલ આપનારને દસલાખ અમેરિકી ડૉલરનું પારિતોષિક અપાય છે. રીમાન હાઇપોથીસિસ નામનો ખૂબ જ અગત્યનો પ્રશ્ન આ યાદી અને હિલ્બર્ટના પ્રશ્નોમાં બન્નેમાં સામેલ છે.

 

કાર્લ ફેડરિક ગાઉસ ગણિતને વિજ્ઞાનની રાણી કહેતા. વિજ્ઞાન માટેનો અંગ્રેજી શબ્દ Science લેટિન ભાષાના scientia અથવા ફ્રેન્ચ ભાષાના science,શબ્દો ઉપરથી આવ્યો છે. મૂળ બંને ભાષામાં તેનો અર્થ જ્ઞાન થાય છે. આમ મૂળભુત ભાષાના સંદર્ભમાં, અંગ્રેજીના સંદર્ભમા તો ગણિતને વિજ્ઞાન તરીકે જોવાય છે પણ હિન્દુ સંસ્કૃતિમાં પણ ગણિત એક વિજ્ઞાન ગણાય છે. વિજ્ઞાનને સ્પેશિયલાઇઝેશનના અર્થમાં જોવાની પ્રણાલિ બહુ જુની નથી. જો સાયન્સને આવા અથવા તો ભૌતિકીય વિજ્ઞાનો પુરતું સીમિત કરી દઇએ તો તેને વિજ્ઞાન ન કહેવાય, ખાસ કરીને પ્યોર ગણિત તો નહીં જ. બીજી તરફ વીસમી સદીના અંતમા ઉપર દર્શાવ્યા પ્રમાણે એલન કોન્સના ગણિતમાં પ્રદાન દ્વારા ક્વોન્ટમ મિકેનિક્સની સાથે બીજા ઘણા ભૌતિક વિજ્ઞાનોને સમજવા ગણિત સિવાય બીજો કોઇ રસ્તો જ નથી આમ ગણિત એ વ્યાપક અર્થમાં વિજ્ઞાનની નવી ભાષા તરીકે પણ ગણાય છે. વીસમી સદીના પૂર્વાર્ધ સુધી ગણિત સામાન્યતઃ ભૌતિક વિજ્ઞાન અને ઇજનેરીવિદ્યામાં વપરાતું પણ વીસમી સદીના ઉત્તરાર્ધમાં તેનો ઉપયોગ ભાષાવિજ્ઞાન, જીવવિજ્ઞાન, અર્થશાસ્ત્ર જેવી જ્ઞાનની શાખાઓમાં ગણિતનો અનિવાર્ય ઉપયોગ પ્રસ્થાપિત થતાં હવે ગણિત જ્ઞાનની શાખાઓમાં સર્વોપરી બની ગયું છે. બીજી તરફ, બેલ

મહાન વૈજ્ઞાનિકોના ગણિત વિશેનાં વિધાનો પણ જાણવા જેવા છે. આલ્બર્ટ આઇનસ્ટાઇનના કહેવા મુજબ"જયારે જ્યારે ગણિતના નિયમો વાસ્તવિકતાની વાત કરે છે, ત્યારે ત્યારે તેમાં ચોકસાઇનો અભાવ હોય છે, અને જ્યારે ગણિત ચોકસાઇપૂર્વક કાંઇક કહે છે ત્યારે તે વાસ્તવિકતાની વાત કરી શકતું નથી."

ઘણાં તત્વચિંતકો માને છે કે ગણિતમાં પ્રાયોગિક ચકાસણીનો અભાવ છે અને તેથી તે કાર્લ પોપર.ની વ્યાખ્યા મુજબ વિજ્ઞાન નથી. જો કે, ૧૯૩૦ના દાયકામાં ગાણિતિક તર્કની દિશામાં થયેલા મહત્વના કામ પછી કાર્લ પોપરે પોતાની માન્યતા બદલતાં કહ્યું કે, "ભૌતિકવિજ્ઞાન, જીવવિજ્ઞાન તેમજ અન્ય વિજ્ઞાનોની જેમજ ગણિતની મોટા ભાગના સિદ્ધાંતો પણ hypothetico-deductive છે તેથી શુદ્ધ ગણિત પણ કુદરતી વિજ્ઞાન છે."

બીજી તરફ મોટા ભાગના ગણિતજ્ઞોની લાગણી અને માન્યતા આ બધા કરતાં જુદી પડે છે. તેઓ માને છે કે ગણિતને વિજ્ઞાન ગણવાથી તેની મહત્તામાં આંચ આવે છે, તે ગણિતને અન્યાયકર્તા છે, તેથી ગણિતની આંતરીક સુંદરતા મરી પરવારે છે અને સાત કળાઓ પૈકી એક તરીકે ઇતિહાસમાં જેની ગણના થઇ છે તેનો ઉપહાસ કરી ગણિતના ઇતિહાસનું મહત્વ ઘટાડે છે. ગણિત તો એક કળા છે. વળી ઘણા ગણિતજ્ઞોના મત મુજબ ગણિત અને વિજ્ઞાનના સમન્વયની અવગણના કરીને આપણે ગણિતને પોતાને વિજ્ઞાન દ્વારા વિકસવાની જે તક મળી તેની સામે એક આંખ મીચામણાં કરી રહ્યા છીએ. આમ ગણિત એ રચના કરેલી (કળા) છે કે કુદરતમાં શોધાયેલુ વિજ્ઞાન છે, તેની ચર્ચા તત્વચિંતનનો એક મોટો અને કાયમનો મુદ્દો છે.

These theorems have interested mathematicians and non-mathematicians alike.

પાયથાગોરસનું પ્રમેય – Fermat's last theorem – Goldbach's conjecture – Twin Prime Conjecture – Gödel's incompleteness theorems – Poincaré conjecture – Cantor's diagonal argument – Four color theorem – Zorn's lemma – Euler's identity – Church-Turing thesis

Important theorems and conjectures

See list of theorems, list of conjectures for more

These are theorems and conjectures that have changed the face of mathematics throughout history.

Riemann hypothesis – Continuum hypothesis – P=NP – Pythagorean theorem – Central limit theorem – Fundamental theorem of calculus – Fundamental theorem of algebra – Fundamental theorem of arithmetic – Fundamental theorem of projective geometry – classification theorems of surfaces – Gauss-Bonnet theorem

Approaches to understanding the nature of mathematics also influence the way mathematicians study their subject.

Philosophy of mathematics – Mathematical intuitionism – Mathematical constructivism – Foundations of mathematics – Set theory – Symbolic logic – Model theory – Category theory – Logic – Reverse Mathematics – Table of mathematical symbols

ગણિત અને સ્થાપત્ય – ગણિત અને શિક્ષણ – Mathematics of musical scales

Mathematics is not a closed intellectual system, in which everything has already been worked out. There is no shortage of open problems.

Pseudomathematics is a form of mathematics-like activity undertaken outside academia: and occasionally by mathematicians themselves. It often consists of determined attacks on famous questions, consisting of proof-attempts made in an isolated way (that is, long papers not supported by previously published theory). The relationship to generally-accepted mathematics is similar to that between pseudoscience and real science. The misconceptions involved are normally based on:

• misunderstanding of the implications of mathematical rigour;
• attempts to get round the usual criteria for publication of mathematical papers in a learned journal after peer review, with assumptions of bias;
• lack of familiarity with, and therefore underestimation of, the existing literature.

The case of Kurt Heegner's work shows that the mathematical establishment is neither infallible, nor unwilling to admit error in assessing 'amateur' work. And like astronomy, mathematics owes much to amateur contributors such as Fermat and Mersenne.

Mathematics is not accountancy. Although arithmetic computation is crucial to accountants, their main concern is to verify that computations are correct through a system of doublechecks. Advances in abstract mathematics are mostly irrelevant to the efficiency of concrete bookkeeping, but the use of computers clearly does matter.

Mathematics is not numerology. Numerology uses modular arithmetic to reduce names and dates down to numbers, but assigns emotions or traits to these numbers intuitively or on the basis of traditions.

• Benson, Donald C., The Moment Of Proof: Mathematical Epiphanies (1999).
• Courant, R. and H. Robbins, What Is Mathematics? (1941);
• Davis, Philip J. and Hersh, Reuben, The Mathematical Experience. Birkhäuser, Boston, Mass., 1980. A gentle introduction to the world of mathematics.
• Boyer, Carl B., History of Mathematics, Wiley, 2nd edition 1998 available, 1st edition 1968 . A concise history of mathematics from the Concept of Number to contemporary Mathematics.
• Gullberg, Jan, Mathematics--From the Birth of Numbers. W.W. Norton, 1996. An encyclopedic overview of mathematics presented in clear, simple language.
• Hazewinkel, Michiel (ed.), Encyclopaedia of Mathematics. Kluwer Academic Publishers 2000. A translated and expanded version of a Soviet math encyclopedia, in ten (expensive) volumes, the most complete and authoritative work available. Also in paperback and on CD-ROM.
• Kline, M., Mathematical Thought from Ancient to Modern Times (1973).
• Pappas, Theoni, The Joy Of Mathematics (1989).