Set Theory Intersection
In set theory, the intersection of two sets A and B , denoted by A ∩ B , is the set containing all elements of A that also belong to B or equivalently, all elements of B that also belong to A .
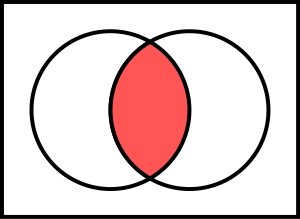 The intersection of two sets and represented by circles. is in red. | |
| Type | Set operation |
|---|---|
| Field | Set theory |
| Statement | The intersection of and is the set of elements that lie in both set and set . |
| Symbolic statement | |
Notation and terminology
Intersection is written using the symbol "





For an explanation of the symbols used in this article, refer to the table of mathematical symbols.
Definition




The intersection of two sets 





That is, 




For example:
- The intersection of the sets {1, 2, 3} and {2, 3, 4} is {2, 3}.
- The number 9 is not in the intersection of the set of prime numbers {2, 3, 5, 7, 11, ...} and the set of odd numbers {1, 3, 5, 7, 9, 11, ...}, because 9 is not prime.
Intersecting and disjoint sets
We say that 












We say that 






For example, the sets 

Algebraic properties
Binary intersection is an associative operation; that is, for any sets 


 . Intersection is also commutative. That is, for any
. Intersection is also commutative. That is, for any  and
and  one has
one has
 ,
, 
 satisfies that
satisfies that  . All these properties follow from analogous facts about logical conjunction.
. All these properties follow from analogous facts about logical conjunction. Intersection distributes over union and union distributes over intersection. That is, for any sets 


 one may define the complement
one may define the complement  of
of  to be the set of all elements of
to be the set of all elements of  not in
not in  Furthermore, the intersection of
Furthermore, the intersection of  and
and  may be written as the complement of the union of their complements, derived easily from De Morgan's laws:
may be written as the complement of the union of their complements, derived easily from De Morgan's laws:
Arbitrary intersections
The most general notion is the intersection of an arbitrary nonempty collection of sets. If 







The notation for this last concept can vary considerably. Set theorists will sometimes write "






In the case that the index set 

When formatting is difficult, this can also be written "
Nullary intersection

The conjunction of no argument is the tautology (compare: empty product); accordingly the intersection of no set is the universe.
In the previous section, we excluded the case where 



 is empty, there are no sets
is empty, there are no sets  in
in  so the question becomes "which
so the question becomes "which  's satisfy the stated condition?" The answer seems to be every possible
's satisfy the stated condition?" The answer seems to be every possible  . When
. When  is empty, the condition given above is an example of a vacuous truth. So the intersection of the empty family should be the universal set (the identity element for the operation of intersection), but in standard (ZF) set theory, the universal set does not exist.
is empty, the condition given above is an example of a vacuous truth. So the intersection of the empty family should be the universal set (the identity element for the operation of intersection), but in standard (ZF) set theory, the universal set does not exist. However, when restricted to the context of subsets of a given fixed set 







Also, in type theory 






See also
- Algebra of sets – Identities and relationships involving sets
- Cardinality – Definition of the number of elements in a set
- Complement – Set of the elements not in a given subset
- Intersection (Euclidean geometry) – Shape formed from points common to other shapes
- Intersection graph – Graph representing intersections between given sets
- Intersection theory – Branch of algebraic geometry
- List of set identities and relations – Equalities for combinations of sets
- Logical conjunction – Logical connective AND
- MinHash – Data mining technique
- Naive set theory – Informal set theories
- Symmetric difference – Elements in exactly one of two sets
- Union – Set of elements in any of some sets
References
Further reading
- Devlin, K. J. (1993). The Joy of Sets: Fundamentals of Contemporary Set Theory (Second ed.). New York, NY: Springer-Verlag. ISBN 3-540-94094-4.
- Munkres, James R. (2000). "Set Theory and Logic". Topology (Second ed.). Upper Saddle River: Prentice Hall. ISBN 0-13-181629-2.
- Rosen, Kenneth (2007). "Basic Structures: Sets, Functions, Sequences, and Sums". Discrete Mathematics and Its Applications (Sixth ed.). Boston: McGraw-Hill. ISBN 978-0-07-322972-0.
External links

This article uses material from the Wikipedia English article Intersection (set theory), which is released under the Creative Commons Attribution-ShareAlike 3.0 license ("CC BY-SA 3.0"); additional terms may apply (view authors). Content is available under CC BY-SA 4.0 unless otherwise noted. Images, videos and audio are available under their respective licenses.
®Wikipedia is a registered trademark of the Wiki Foundation, Inc. Wiki English (DUHOCTRUNGQUOC.VN) is an independent company and has no affiliation with Wiki Foundation.
