Mathematik Beweis: Logische Begründung einer mathematischen Aussage

der Unrichtigkeit einer Aussage aus einer Menge von Axiomen, die als wahr vorausgesetzt werden, und anderen Aussagen, die bereits bewiesen sind. Man spricht daher auch von axiomatischen Beweisen.

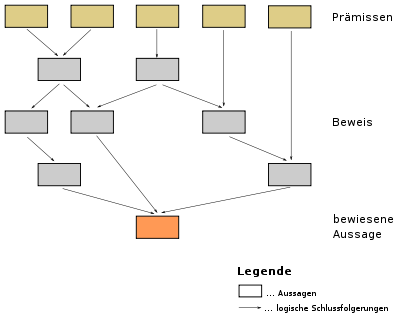
Umfangreichere Beweise von mathematischen Sätzen werden in der Regel in mehrere kleine Teilbeweise aufgeteilt, siehe dazu Satz und Hilfssatz.

In der Beweistheorie, einem Teilgebiet der mathematischen Logik, werden Beweise formal als Ableitungen aufgefasst und selbst als mathematische Objekte betrachtet, um etwa die Beweisbarkeit oder Unbeweisbarkeit von Sätzen aus gegebenen Axiomen selbst zu beweisen.

Existenzbeweise

Bei einem konstruktiven Existenzbeweis wird entweder die Lösung selbst genannt, deren Existenz zu zeigen ist, oder ein Verfahren angegeben, das zur Lösung führt, das heißt, es wird eine Lösung konstruiert.

Bei einem nicht-konstruktiven Beweis wird anhand von Eigenschaften auf die Existenz einer Lösung geschlossen. Manchmal wird sogar indirekt die Annahme, es gäbe keine Lösung, zum Widerspruch geführt, woraus folgt, dass es eine Lösung gibt. Aus solchen Beweisen geht nicht hervor, wie man die Lösung gewinnt.

Ein einfaches Beispiel soll dies verdeutlichen.

Behauptung: Die Funktion ${\displaystyle f}$  mit ${\displaystyle f(x)=2x-1}$  besitzt im Intervall ${\displaystyle [0,1]}$  mindestens eine Nullstelle ${\displaystyle x_{0}}$ .

Konstruktiver Beweis: Sei ${\displaystyle x_{0}=0{,}5}$ . Dann gilt ${\displaystyle f(x_{0})=2\cdot x_{0}-1=2\cdot 0{,}5-1=1-1=0}$ . Ferner liegt ${\displaystyle x_{0}=0{,}5}$  im Intervall ${\displaystyle [0,1]}$ . Damit ist die Behauptung bewiesen. Die Nullstelle ist sogar mit ${\displaystyle x_{0}=0{,}5}$  angegeben.

Nicht-konstruktiver Beweis: ${\displaystyle f}$  ist stetig. Ferner ist ${\displaystyle f(0)=-1<0}$  und ${\displaystyle f(1)=1>0}$ . Nach dem Zwischenwertsatz für stetige Funktionen folgt die Behauptung. Über den Wert der Nullstelle liefert dieser Beweis jedoch keine Information.

Mengenlehre

In der auf dem Axiomensystem ZFC aufbauenden Mengenlehre nennt man Beweise nicht-konstruktiv, wenn sie das Auswahlaxiom verwenden. Denn alle anderen Axiome von ZFC beschreiben, welche Mengen es gibt bzw. was man mit Mengen machen kann, und geben die konstruierten Mengen an. Nur das Auswahlaxiom postuliert die Existenz einer gewissen Auswahlmöglichkeit, ohne anzugeben, wie diese Auswahl auszuführen wäre. In der Anfangszeit der Mengenlehre war das Auswahlaxiom wegen seines nicht-konstruktiven Charakters heftig umstritten (der mathematische Konstruktivismus vermeidet bewusst das Auswahlaxiom), daher rührt seine Sonderstellung nicht nur in der abstrakten Mengenlehre, sondern auch bei Beweisen in anderen Teilgebieten der Mathematik. In diesem Sinne gelten alle Beweise, die das Lemma von Zorn verwenden, als nicht-konstruktiv, denn dieses Lemma ist äquivalent zum Auswahlaxiom.

Die gesamte Mathematik kann im Wesentlichen auf ZFC aufgebaut und im Rahmen von ZFC bewiesen werden. Über die Grundlagen der Mengenlehre legt der arbeitende Mathematiker in der Regel keine Rechenschaft ab, lediglich die Verwendung des Auswahlaxioms findet Erwähnung, in der Regel in der Form des Lemmas von Zorn. Darüber hinausgehende mengentheoretische Annahmen werden stets angegeben, zum Beispiel wenn man die Kontinuumshypothese oder ihre Negation verwendet.

Formale Beweise reduzieren die Beweisschritte auf eine Reihe definierter Operationen auf Zeichenketten. Solche Beweise können in der Regel nur mit Maschinenunterstützung erstellt werden (siehe etwa Coq (Software)) und sind für Menschen kaum lesbar, schon allein die Übertragung der zu beweisenden Sätze in eine rein formale Sprache führt zu sehr langen, umständlichen und unverständlichen Zeichenketten. Eine Reihe bekannter Sätze wurde inzwischen formalisiert und deren formaler Beweis maschinell überprüft. In der Regel genügt den Mathematikern jedoch die Gewissheit, dass ihre Argumentationsketten prinzipiell in formale Beweise übertragbar wären, ohne dass dies tatsächlich ausgeführt wird, sie verwenden die im Folgenden vorgestellten Beweismethoden.

Einige mathematische Sätze oder logische Schlussregeln lassen sich für eine Vielzahl von Beweisen einsetzen und beeinflussen die Struktur des Beweises besonders stark. Die systematische Vorgehensweise zur Anwendung dieser bezeichnet man dann als Beweismethode, Beweisverfahren, Beweistechnik oder Beweisprinzip. Die Gültigkeit einer Beweismethode bedarf selbst eines Beweises, im Rahmen der Axiome und der Logik gültig zu sein (etwa ist die Reductio ad absurdum (s. u.) in der Grundform nicht in intuitionistischer Logik, und eine transfinite Induktion über alle Kardinalzahlen nur unter Voraussetzung des Wohlordnungssatzes möglich). Hier eine Auswahl von Standard-Beweismethoden:

Direkter Beweis

Für einen direkten Beweis (direkter Schluss) nimmt man einen bereits als richtig bewiesenen Satz (Prämisse) und leitet, durch logische Schlussfolgerungen, daraus den zu beweisenden Satz (Konklusion) ab. Als einfaches Beispiel diene Folgendes:

Behauptung: Das Quadrat einer ungeraden natürlichen Zahl ${\displaystyle n}$  ist stets ungerade.

Beweis: Es sei ${\displaystyle n}$  eine ungerade natürliche Zahl. Das heißt, ${\displaystyle n}$  lässt sich darstellen als ${\displaystyle n=2k+1}$ , wobei ${\displaystyle k}$  eine natürliche Zahl oder Null ist. Daraus folgt mit Hilfe der ersten binomischen Formel

${\displaystyle n^{2}=(2k+1)^{2}=4k^{2}+4k+1=2\cdot (2k^{2}+2k)+1}$ .

Aus der Möglichkeit, ${\displaystyle n^{2}}$  so darzustellen folgt, dass ${\displaystyle n^{2}}$  ungerade ist.

Indirekter Beweis

Bei einem indirekten Beweis (Reductio ad absurdum, Widerspruchsbeweis) zeigt man, dass ein Widerspruch entsteht, wenn die zu beweisende Behauptung falsch wäre. Dazu nimmt man an, dass die Behauptung falsch ist, und wendet dann die gleichen Methoden wie beim direkten Beweis an. Wenn daraus ein Widerspruch entsteht, dann kann die Behauptung nicht falsch sein, also muss sie richtig sein (Satz vom ausgeschlossenen Dritten).

Nun ein Beispiel für eine reductio ad absurdum:

Behauptung: Ist die Wurzel aus einer geraden natürlichen Zahl ${\displaystyle n}$  eine natürliche Zahl, so ist diese gerade.

Beweis: Angenommen, ${\displaystyle {\sqrt {n}}=k}$  wäre ungerade. Dann ist auch ${\displaystyle k^{2}=n}$  ungerade (siehe obiges Beispiel zum direkten Beweis), und das ist ein Widerspruch zu der Voraussetzung, dass ${\displaystyle n}$  gerade ist. Also ist die getroffene Annahme falsch, das heißt, ${\displaystyle {\sqrt {n}}}$  ist gerade.

Ein weiteres klassisches Beispiel:

Behauptung: Die Zahl ${\displaystyle {\sqrt {2}}}$  ist irrational.

Beweis: Angenommen, diese Zahl wäre rational. Dann kann man sie als Bruch ${\displaystyle {\sqrt {2}}={\tfrac {l}{k}}}$  darstellen, wobei ${\displaystyle l}$  und ${\displaystyle k}$  natürliche Zahlen und ohne Beschränkung der Allgemeinheit teilerfremd sind (sonst kann man den Bruch soweit kürzen, bis das der Fall ist). Daraus folgt durch Quadrieren

${\displaystyle 2={\frac {l^{2}}{k^{2}}}\,}$  , also ${\displaystyle \,l^{2}=2k^{2}.}$ 

Folglich ist ${\displaystyle l^{2}}$  eine gerade Zahl. Da die Wurzel aus einer geraden Quadratzahl auch gerade ist (siehe vorangegangene Behauptung), ist ${\displaystyle l}$  selbst gerade, also ist ${\displaystyle {\tfrac {l}{2}}}$  eine natürliche Zahl. Durch Umformung der letzten Gleichung erhält man

${\displaystyle k^{2}={\frac {l^{2}}{2}}=2\cdot \left({\frac {l}{2}}\right)^{2}.}$ 

Das zeigt, dass ${\displaystyle k^{2}}$  und somit auch ${\displaystyle k}$  gerade natürliche Zahlen sind. Also sind ${\displaystyle l}$  und ${\displaystyle k}$  beide gerade und haben somit beide den Teiler 2. Damit sind ${\displaystyle l}$  und ${\displaystyle k}$  nicht teilerfremd – im Widerspruch zu der Annahme ihrer Teilerfremdheit. Also ist auch die ursprüngliche Annahme, ${\displaystyle {\sqrt {2}}}$  sei rational, falsch.

Die vorangegangenen Beispiele sind nicht darauf angewiesen, dass das Prinzip vom ausgeschlossenen Dritten zur Verfügung steht, wenn man „x ist irrational“ als „x ist nicht rational“ definiert. Was die Form angeht, ist das zweite eher ein direkter Beweis einer Negation.

Ein Beispiel, für das tatsächlich klassische Logik benötigt wird (und wir verwenden das Prinzip des indirekten Beweises ineffizienterweise zunächst ausschließlich ganz außen):

Behauptung: (C): ${\displaystyle \lnot (\alpha \to \beta )\to \alpha }$ .

Beweis: Wir nehmen die Negation von (C), also (A): ${\displaystyle \lnot (\lnot (\alpha \to \beta )\to \alpha )}$ , an und führen diese Annahme zu einem Widerspruch: Zunächst gilt (B): ${\displaystyle \alpha \to \beta }$ , denn ${\displaystyle \alpha }$  angenommen, gilt natürlich auch ${\displaystyle \lnot (\alpha \to \beta )\to \alpha }$ , was (A) widerspricht. Daher gilt aber auch (C), denn, ${\displaystyle \lnot (\alpha \to \beta )}$  angenommen, haben wir einen Widerspruch zu (B). (C) widerspricht nun offenbar der Annahme (A), wir haben also den gewünschten Widerspruch.

Besserer Beweis: Wir nehmen ${\displaystyle \lnot (\alpha \to \beta )}$  an und zeigen unter dieser Annahme ${\displaystyle \alpha }$ , indem wir ${\displaystyle \lnot \alpha }$  zu einem Widerspruch führen: Gilt nämlich ${\displaystyle \lnot \alpha }$ , dann auch ${\displaystyle \alpha \to \beta }$ , weil die Annahme von ${\displaystyle \alpha }$  zu einem Widerspruch führt. ${\displaystyle \alpha \to \beta }$  widerspricht dann aber der globalen Annahme.

An diesem Beispiel sieht man einen Hinweis zur Pragmatik des Beweisfindens: In der Regel ist es von Vorteil, das Prinzip des indirekten Beweisens möglichst spät anzuwenden und so lange, wie es geht, Pfade zum Finden direkter Beweise zu verfolgen. Überdies zeigt die Beweistheorie, dass man durch Verfolgen der Strategie, das Prinzip des indirekten Beweisens möglichst spät anzuwenden, und dabei keine unmotivierten Wahlen zu treffen, nicht in einer Situation landen kann, in der man Unmögliches zu beweisen hat, ein früheres Abbiegen auf einen Pfad zu einem indirekten (Teil-)Beweis aber von Erfolg gekrönt gewesen wäre.

Vollständige Induktion

 

Der Beweis durch vollständige Induktion ist ein oft angewendetes Verfahren zum Beweis von Sätzen der Form „Für jede natürliche Zahl ${\displaystyle n}$  gilt …“. Dazu zeigt man zuerst, dass die Aussage für ${\displaystyle n=0}$  (oder auch einen anderen Anfangswert ${\displaystyle n_{0}}$ ) gilt, und danach, dass sie immer auch für ${\displaystyle n+1}$  gilt, wenn sie für ein ${\displaystyle n}$  gilt. Die vollständige Induktion lässt sich mit einem Domino-Effekt veranschaulichen. Man stellt die Steine so auf, dass, wenn einer umfällt, auch immer der nächste umfällt (${\displaystyle n}$  → ${\displaystyle n+1}$ ), und stößt den ersten Stein um (${\displaystyle n=0}$ ).

Ein einfaches Beispiel:

Behauptung: Es gilt für alle natürlichen Zahlen ${\displaystyle n}$ : ${\displaystyle 1+3+\dotsb +(2n+1)=(n+1)^{2}}$ 

Beweis:

1. Die Behauptung gilt für ${\displaystyle n=0}$ : ${\displaystyle (2\cdot 0+1)=1=(0+1)^{2}}$  ist eine wahre Aussage.
2. Die Behauptung sei für ein ${\displaystyle n}$  gültig. Für ${\displaystyle n+1}$  untersucht man die Summe

${\displaystyle 1+3+\dotsb +(2n+1)+(2n+3)}$ 
Da die Behauptung für ${\displaystyle n}$  gültig ist, folgt
${\displaystyle {\begin{aligned}1+3+\dotsb +(2n+1)+(2n+3)&=(n+1)^{2}+(2n+3)\\&=(n+1)^{2}+2(n+1)+1\\&=((n+1)+1)^{2}\end{aligned}}}$ 
Also gilt die Behauptung auch für ${\displaystyle n+1}$ , damit ist die Aussage nach dem Induktionsprinzip bewiesen.

Vollständige Fallunterscheidung

Bei einem Beweis durch vollständige Fallunterscheidung (engl. proof by exhaustion „durch Ausschöpfung“) wird jeder der möglichen Fälle einzeln betrachtet. Die Zahl der möglichen Fälle muss daher endlich sein.

Behauptung: Jede Primzahl ${\displaystyle p\geq 3}$  hat die Form ${\displaystyle p=4\cdot k\pm 1}$  mit einer natürlichen Zahl ${\displaystyle k}$ .

Beweis: Man unterscheidet folgende vier Fälle für die Zahl ${\displaystyle p}$ , von denen immer genau einer eintritt:

1. ${\displaystyle p=4k}$ 
2. ${\displaystyle p=4k+1}$ 
3. ${\displaystyle p=4k+2}$ 
4. ${\displaystyle p=4k+3=4(k+1)-1}$ 

Im ersten dieser Fälle ist ${\displaystyle p}$  durch 4 teilbar und damit keine Primzahl, im dritten Fall ist ${\displaystyle p}$  durch 2 teilbar und somit ebenfalls keine Primzahl. Also muss einer der Fälle zwei oder vier eintreten, das heißt, ${\displaystyle p}$  hat die Form ${\displaystyle p=4\cdot k\pm 1}$  mit einer natürlichen Zahl ${\displaystyle k}$ .

Es sei angemerkt, dass die Fallunterscheidung zwar vollständig sein muss, aber die untersuchten Fälle sich nicht gegenseitig ausschließen müssen.

Diagonalverfahren

Die Diagonalverfahren wurden von Georg Cantor zum Beweis zweier spezieller Aussagen entwickelt. Sie haben sich seitdem als allgemeine Beweismethoden bewährt.

Das erste Cantorsche Diagonalverfahren ist ein direkter Beweis für die Abzählbarkeit einer Menge. Es wird gezeigt, dass man jedem Element der zu untersuchenden Menge eine natürliche Zahl zuordnen kann.

Das zweite Cantorsche Diagonalverfahren ist ein indirekter Beweis für die Überabzählbarkeit einer Menge. Es wird also das Gegenteil angenommen, nämlich dass die Menge abzählbar wäre. Dann wird aus dieser Annahme ein Widerspruch hergeleitet, sodass sie fallen gelassen werden muss.

Schubfachprinzip/Taubenschlagprinzip

Das Schubfachprinzip geht auf den deutschen Mathematiker Dirichlet zurück und kann sehr anschaulich formuliert werden: Verteilt man ${\displaystyle n+1}$  Gegenstände auf ${\displaystyle n}$  Schubfächer, dann befinden sich in mindestens einem Schubfach mindestens zwei Gegenstände. Als Beispiel betrachten wir:

Behauptung: Hat ${\displaystyle A\subset \{1,2,\ldots ,2n\}}$  mindestens ${\displaystyle n+1}$  Elemente, so gibt es ${\displaystyle a,b\in A}$  mit ${\displaystyle a|b}$ .

Beweis: Alle Elemente aus ${\displaystyle A}$  haben die Gestalt ${\displaystyle 2^{k}m}$  mit einer ungeraden Zahl ${\displaystyle m}$ . Von diesen gibt es aber nur ${\displaystyle n}$  verschiedene in ${\displaystyle \{1,2,\ldots ,2n\}}$ , so dass eine ungerade Zahl bei obiger Zerlegung der mindestens ${\displaystyle n+1}$  Zahlen aus ${\displaystyle A}$  zweimal vorkommen muss (das ist das Schubfachprinzip). Daher enthält ${\displaystyle A}$  zwei Zahlen ${\displaystyle 2^{k}m}$  und ${\displaystyle 2^{l}m}$  mit derselben ungeraden Zahl ${\displaystyle m}$ . Offenbar teilt die kleinere die größere.

Transfinite Induktion

Bei der transfiniten Induktion wird die vollständige Induktion auf beliebige wohlgeordnete Klassen verallgemeinert.

Häufig hat man es mit Aussagen über alle Ordinalzahlen zu tun. Wie auch bei der oben vorgestellten vollständigen Induktion in ${\displaystyle \mathbb {N} }$  muss man die Behauptung für die erste Ordinalzahl 0 beweisen, und dann, dass, wenn die Behauptung für eine Ordinalzahl vorausgesetzt wird, sie auch für deren Nachfolger gilt. Im Gegensatz zu obiger Induktion muss man zusätzlich zeigen, dass die Behauptung auch für jede Limesordinalzahl gilt, wenn sie für alle kleineren Ordinalzahlen zutrifft. Verzichtet man auf diesen zusätzlichen Teil, so funktioniert die transfinite Induktion nur bis unterhalb der ersten Limesordinalzahl, das heißt nur für die Ordinalzahlen ${\displaystyle 0,1,2,\ldots }$ . Man erhält dann die gewöhnliche vollständige Induktion in den natürlichen Zahlen, denn diese sind die Ordinalzahlen bis zur ersten Limesordinalzahl.

In der Maßtheorie

Das Prinzip der guten Mengen wird in der Maßtheorie verwendet, um zu beweisen, dass eine Aussage für alle Elemente einer σ-Algebra oder eines anderen Mengensystems zutrifft. Außerdem bedient man sich der maßtheoretische Induktion als Beweismethode, um Aussagen für eine vorgegebene Menge von messbaren Funktionen zu zeigen.

In der homologischen Algebra

Ein Beweisverfahren der homologischen Algebra ist die Diagrammjagd. Sie findet u. a. bei den Beweisen des Fünferlemmas, des Schlangenlemmas oder des Neunerlemmas Anwendung.

Neben den Beweismethoden gibt es einige hilfreiche Beweisstrategien: Entscheidet man sich beim Beweis einer Aussage für eine der oben beschriebenen Methoden, so hilft bei der Umsetzung dieser Methode eine Beweisstrategie.

Extremalprinzip

Das Extremalprinzip tritt insbesondere bei Existenzbeweisen auf: Genauer immer dann, wenn es darum geht, die Existenz eines Objekts innerhalb einer Menge zu beweisen. Das allgemeine Extremalprinzip knüpft an der Idee an, das dort, wo etwas extremal (etwa größtmöglich, kleinstmöglich usw.) wird, besondere Strukturen entstehen, aus denen im Rahmen der mathematischen Beweisführung wertvolle Fakten abgeleitet werden können. Diese Extremalität findet sich in der Mathematik häufig, etwa in folgenden Eigenschaften:

• Jede nichtleere, nach oben beschränkte Teilmenge reeller Zahlen besitzt ein Supremum, d. h. eine kleinste obere Schranke (Supremumseigenschaft). Umgekehrt besitzt eine nach unten beschränkte, nichtleere Teilmenge der reellen Zahlen ein Infimum, also eine größte untere Schranke.
• Jede nichtleere Menge natürlicher Zahlen enthält eine kleinste Zahl. (Wohlordnungsprinzip)

Invarianzprinzip

Das Invarianzprinzip folgt dem Grundsatz, ein Hauptaugenmerk auf dasjenige zu richten, was invariant (d. h. unverändert) unter Veränderung bleibt. Oft versteht man ein komplexes System besser, wenn man versteht, wie sich dessen Einzelteile verhalten. Das Invarianzprinzip ist hilfreich für Unmöglichkeitsbeweise.

Nahrhafte Null

Beweise in der Analysis bedienen sich oft der Strategie des „Hinzuaddierens einer nahrhaften Null“. Der Zusatz „nahrhaft“ rührt daher, dass das Addieren einer Null einen Ausdruck zwar nicht verändert, allerdings in einigen Fällen nahrhaften Boden für eine elegante algebraische Umformung bietet.

Beispiel

Möchte man zeigen, dass jede konvergente Folge eine Cauchy-Folge ist, so bedient man sich einer nahrhaften Null ${\displaystyle 0=a-a}$ , um die Dreiecksungleichung auszunutzen. Sei ${\displaystyle (a_{n})_{n\in \mathbb {N} }}$  eine beliebige konvergente Folge und ${\displaystyle a}$  ihr Grenzwert. Sei ${\displaystyle \varepsilon >0}$ , dann gibt es nach Definition der (Folgen-)Konvergenz ein ${\displaystyle N\in \mathbb {N} }$  mit ${\displaystyle |a-a_{n}|<{\frac {\varepsilon }{2}}}$  und ${\displaystyle |a-a_{m}|<{\frac {\varepsilon }{2}}}$  für alle ${\displaystyle n,m\geq N}$ . Sei ${\displaystyle n,m\geq N}$  nun beliebig, so gilt:

${\displaystyle |a_{n}-a_{m}|=|a_{n}\overbrace {-a+a} ^{=0}-a_{m}|=|(a_{n}-a)+(a-a_{m})|\leq |a_{n}-a|+|a_{m}-a|<{\frac {\varepsilon }{2}}+{\frac {\varepsilon }{2}}=\varepsilon }$ 

Somit ist jede konvergente Folge sogleich eine Cauchy-Folge, was zu beweisen war. Der Beweis lebt vom Hinzuaddieren einer nahrhaften Null im zweiten Schritt.

• Beweis (Logik)
• Ableitung (Logik)
• Quod erat demonstrandum

• Martin Aigner, Günter M. Ziegler: Das BUCH der Beweise. Springer, Berlin 2004, ISBN 3-540-40185-7
• Wolfgang Rautenberg: Einführung in die Mathematische Logik. 3. Auflage. Vieweg+Teubner, Wiesbaden 2008, ISBN 978-3-8348-0578-2, doi:10.1007/978-3-8348-9530-1. 

 

Wikibooks: Mathe für Nicht-Freaks: Beweis – Lern- und Lehrmaterialien

 

Wikibooks: Beweisarchiv – Lern- und Lehrmaterialien

• Die Zeit: Obst in Formeln (zur Problematik eines Beweises mit Computer)
• Zusammenfassung der Beweismethoden für Schüler
• Die wichtigsten Beweise der Schulmathematik
• Landesbildungsserver BW: Dynamische Arbeitsblätter zu geometrischen Beweisen