Distribución Normal

Distribución normal
La llinia verde correspuende a la distribución normal estándar Función de densidá de probabilidá
Función de distribución de probabilidá
Parámetros	${\displaystyle \mu \in \mathbb {R} \,\!}$ ${\displaystyle \sigma >0\,\!}$
Función de densidá (pdf)	${\displaystyle {\frac {1}{\sigma {\sqrt {2\pi }}}}\;y^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}\,\!}$
Función de distribución (cdf)	${\displaystyle {\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]}$
Media	${\displaystyle \mu \,\!}$
Mediana	${\displaystyle \mu \,\!}$
Moda	${\displaystyle \mu \,\!}$
Varianza	${\displaystyle \sigma ^{2}\,\!}$
Coeficiente de simetría	0
Curtosis	0
Entropía	${\displaystyle \ln \left(\sigma {\sqrt {2\,\pi \,y}}\right)\,\!}$
Función xeneradora de momentos (mgf)	${\displaystyle M_{X}(t)=y^{\mu \,t+{\frac {\sigma ^{2}t^{2}}{2}}}\,\!}$
Función característica	${\displaystyle \chi _{X}(t)=y^{\mu \,i\,t-{\frac {\sigma ^{2}t^{2}}{2}}}\,\!}$
[editar datos en Wikidata]

La gráfica de la so función de densidá tien una forma acampanada y ye simétrica respectu d'un determináu parámetru estadísticu. Esta curva conozse como campana de Gauss y ye el gráficu d'una función gaussiana.

La importancia d'esta distribución anicia en que dexa modelar numberosos fenómenos naturales, sociales y psicolóxicos.Ente que los mecanismos que subyacen a gran parte d'esti tipu de fenómenos son desconocíos, pola enorme cantidá de variables incontrolables que nellos intervienen, l'usu del modelu normal puede xustificase asumiendo que cada observación llógrase como la suma d'unes poques causes independientes.

Ello ye que la estadística descriptiva namái dexa describir un fenómenu, ensin esplicación dalguna. Pa la esplicación causal ye precisu'l diseñu esperimental, d'ende que al usu de la estadística en psicoloxía y socioloxía seya conocíu como métodu correlacional.

La distribución normal tamién ye importante pola so rellación cola estimación por mínimos cuadraos, unu de los métodos d'estimación más simples y antiguos.

Dellos exemplos de variables acomuñaes a fenómenos naturales que siguen el modelu de la normal son:

• calteres morfolóxicos d'individuos como la estatura;
• calteres fisiolóxicos como l'efeutu d'un fármacu;
• calteres sociolóxicos como'l consumu de ciertu productu por un mesmu grupu d'individuos;
• calteres psicolóxicos como'l cociente intelectual;
• nivel de ruiu en telecomunicaciones;
• errores cometíos al midir ciertes magnitúes;
• etc.

La distribución normal tamién apaez en munches árees de la mesma estadística. Por casu, la distribución muestral de les medies muestrales ye aproximao normal, cuando la distribución de la población de la cual estrayer la muestra nun ye normal. Amás, la distribución normal maximiza la entropía ente toles distribuciones con media y varianza conocíes, lo cual convertir na eleición natural de la distribución subxacente a una llista de datos resumíos en términos de media muestral y varianza. La distribución normal ye la más estendida n'estadística y munchos tests estadísticos tán basaos nuna "normalidá" más o menos xustificada de la variable aleatoria so estudiu.

En probabilidá, la distribución normal apaez como la llende de delles distribuciones de probabilidá continues y discretes.

 

La distribución normal foi presentada per primer vegada por Abraham de Moivre nun artículu del añu 1733, que foi reimpreso na segunda edición de la so The Doctrine of Chances, de 1738, nel contestu de ciertu aproximamientu de la distribución binomial para grandes valores de n. La so resultancia foi ampliáu por Laplace nel so llibru Teoría analítica de les probabilidaes (1812), y na actualidá llámase Teorema de De Moivre-Laplace.

Laplace usó la distribución normal nel analís d'errores d'esperimentos. L'importante métodu de mínimos cuadraos foi introducíu por Legendre en 1805. Gauss, qu'afirmaba usar el métodu dende 1794, xustificar rigorosamente en 1809 asumiendo una distribución normal de los errores. El nome de Gauss acomuñóse a esta distribución porque la usó con mapa cuando analizaba datos astronómicos y dellos autores atribúyen-y un descubrimientu independiente del de De Moivre.Esta atribución del nome de la distribución a una persona distinta del so primer descubridor ye un claru exemplu de la llei de Stigler.

El nome de "campana" vien d'Esprit Jouffret qu'usó'l términu "bell surface" (superficie campana) per primer vegada en 1872 pa una distribución normal bivariante de componentes independientes. El nome de "distribución normal" foi dau independientemente por Charles S. Peirce, Francis Galton y Wilhelm Lexis escontra 1875.^{[ensin referencies]} A pesar d'esta terminoloxía, otres distribuciones de probabilidá podríen ser más apropiaes en determinaos contestos; vease'l discutiniu sobre incidencia, más embaxo.

La función de distribución de la distribución normal ta definida como sigue:

${\displaystyle {\begin{aligned}\Phi _{\mu ,\sigma ^{2}}(x)&{}=\int _{-\infty }^{x}\varphi _{\mu ,\sigma ^{2}}(o)\,du\\&{}={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{x}y^{-{\frac {(o-\mu )^{2}}{2\sigma ^{2}}}}\,du,\quad x\in \mathbb {R} \\\end{aligned}}}$ 

Poro, la función de distribución de la normal estándar ye:

${\displaystyle \Phi (x)=\Phi _{0,1}(x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}y^{-{\frac {o^{2}}{2}}}\,du,\quad x\in \mathbb {R} .}$ 

Esta función de distribución puede espresase en términos d'una función especial llamada función error de la siguiente forma:

${\displaystyle \Phi (x)={\frac {1}{2}}{\Bigl [}1+\operatorname {erf} {\Bigl (}{\frac {x}{\sqrt {2}}}{\Bigr )}{\Bigr ]},\quad x\in \mathbb {R} ,}$ .

y la mesma función de distribución puede, poro, espresase asina:

${\displaystyle \Phi _{\mu ,\sigma ^{2}}(x)={\frac {1}{2}}{\Bigl [}1+\operatorname {erf} {\Bigl (}{\frac {x-\mu }{\sigma {\sqrt {2}}}}{\Bigr )}{\Bigr ]},\quad x\in \mathbb {R} .}$ 

El complementu de la función de distribución de la normal estándar, ${\displaystyle 1-\Phi (x)}$ , se denota con frecuencia ${\displaystyle Q(x)}$ , y ye referida, dacuando, como a cencielles función Q, especialmente en testos d'inxeniería. Esto representa la cola de probabilidá de la distribución gaussiana. Tamién s'usen dacuando otres definiciones de la función Q, que son toes elles tresformamientos simples de ${\displaystyle \Phi }$ .

La inversa de la función de distribución de la normal estándar (función cuantil) puede espresase en términos de la inversa de la función d'error:

${\displaystyle \Phi ^{-1}(p)={\sqrt {2}}\;\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1),}$ .

y l'inversa de la función de distribución puede, poro, espresase como:

${\displaystyle \Phi _{\mu ,\sigma ^{2}}^{-1}(p)=\mu +\sigma \Phi ^{-1}(p)=\mu +\sigma {\sqrt {2}}\;\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1).}$ 

Esta función cuantil llámase dacuando la función probit. Nun hai una primitiva elemental pa la función probit. Esto nun quier dicir puramente que nun se conoz, sinón que se probó la inesistencia de tal función. Esisten dellos métodos exactos p'averar la función cuantil por aciu la distribución normal (vease función cuantil).

Los valores Φ(x) pueden averase con muncha precisión por distintos métodos, tales como integración numbérica, series de Taylor, series asintóticas y fracciones continues.

Llende inferior y superior estrictos pa la función de distribución

Pa grandes valores de x la función de distribución de la normal estándar ${\displaystyle \scriptstyle \Phi (x)}$  ye bien próxima a 1 y ${\displaystyle \scriptstyle \Phi (-x)\,{=}\,1\,{-}\,\Phi (x)}$  ta mui cerca de 0. Les llendes elementales

${\displaystyle {\frac {x}{1+x^{2}}}\varphi (x)<1-\Phi (x)<{\frac {\varphi (x)}{x}},\qquad x>0,}$ .

en términos de la densidá ${\displaystyle \scriptstyle \varphi }$  son útiles.

Usando'l camudo de variable v = o²/2, la llende cimera llógrase como sigue:

${\displaystyle {\begin{aligned}1-\Phi (x)&=\int _{x}^{\infty }\varphi (o)\,du\\&<\int _{x}^{\infty }{\frac {u}{x}}\varphi (o)\,du=\int _{x^{2}/2}^{\infty }{\frac {y^{-v}}{x{\sqrt {2\pi }}}}\,dv=-{\biggl .}{\frac {y^{-v}}{x{\sqrt {2\pi }}}}{\biggr |}_{x^{2}/2}^{\infty }={\frac {\varphi (x)}{x}}.\end{aligned}}}$ 

De forma similar, usando ${\displaystyle \scriptstyle \varphi '(o)\,{=}\,-o\,\varphi (o)}$  y la regla del cociente,

${\displaystyle {\begin{aligned}{\Bigl (}1+{\frac {1}{x^{2}}}{\Bigr )}(1-\Phi (x))&={\Bigl (}1+{\frac {1}{x^{2}}}{\Bigr )}\int _{x}^{\infty }\varphi (o)\,du\\&=\int _{x}^{\infty }{\Bigl (}1+{\frac {1}{x^{2}}}{\Bigr )}\varphi (o)\,du\\&>\int _{x}^{\infty }{\Bigl (}1+{\frac {1}{o^{2}}}{\Bigr )}\varphi (o)\,du=-{\biggl .}{\frac {\varphi (o)}{o}}{\biggr |}_{x}^{\infty }={\frac {\varphi (x)}{x}}.\end{aligned}}}$ 

Resolviendo pa ${\displaystyle \scriptstyle 1\,{-}\,\Phi (x)\,}$  apurre la llende inferior.

Funciones generatrices

Función generatriz de momentos

La función generatriz de momentos defínese como la esperanza de y^(tX). Pa una distribución normal, la función generatriz de momentos ye:

${\displaystyle M_{X}(t)=\mathrm {Y} \left[y^{tX}\right]=\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}y^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}y^{tx}\,dx=y^{\mu t+{\frac {\sigma ^{2}t^{2}}{2}}}}$ 

como puede comprobase al completar el cuadráu nel esponente.

Función carauterística

La función carauterística defínese como la esperanza de y^itX, onde i ye la unidá imaxinaria. D'esta miente, la función carauterística llógrase reemplazando t por it na función generatriz de momentos. Pa una distribución normal, la función carauterística ye

${\displaystyle {\begin{aligned}\chi _{X}(t;\mu ,\sigma )&{}=M_{X}(it)=\mathrm {Y} \left[y^{itX}\right]\\&{}=\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}y^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}y^{itx}\,dx\\&{}=y^{i\mu t-{\frac {\sigma ^{2}t^{2}}{2}}}.\end{aligned}}}$ 

Delles propiedaes de la distribución normal son les siguientes:

1. Ye simétrica respectu de la so media, ${\displaystyle \mu }$ ;

    

2. La moda y la mediana son dambes iguales a la media, ${\displaystyle \mu }$ ;
3. Los punto d'inflexón de la curva dar pa ${\displaystyle x=\mu -\sigma }$  y ${\displaystyle x=\mu +\sigma }$ .
4. Distribución de probabilidá nuna redolada de la media:
   1. nel intervalu ${\displaystyle [\mu -\sigma ,\mu +\sigma ]}$ atópase entendida, aproximao, el 68,26% de la distribución;
   2. nel intervalu ${\displaystyle [\mu -2\sigma ,\mu +2\sigma ]}$  atópase, aproximao, el 95,44% de la distribución;
   3. pela so parte, nel intervalu ${\displaystyle [\mu -3\sigma ,\mu +3\sigma ]}$  atópase entendida, aproximao, el 99,74% de la distribución. Estes propiedaes son de gran utilidá pal establecimientu d'intervalo d'enfotu. Per otra parte, el fechu de que práuticamente la totalidá de la distribución atopar a tres desviación típiques de la media xustifica les llendes de les tables emplegaes davezu na normal estándar.
5. Si ${\displaystyle X\sim N(\mu ,\sigma ^{2})}$  y ${\displaystyle a,b\in \mathbb {R} }$ , entós ${\displaystyle aX+b\sim N(a\mu +b,a^{2}\sigma ^{2})}$ .
6. Si ${\displaystyle X\sim N(\mu _{X},\sigma _{X}^{2})}$  y ${\displaystyle Y\sim N(\mu _{Y},\sigma _{Y}^{2})}$  son variables aleatories normales independientes, entós:
   • La so suma ta de normal distribuyida con ${\displaystyle O=X+Y\sim N(\mu _{X}+\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$  (demostración). Recíprocamente, si dos variables aleatories independientes tienen una suma de normal distribuyida, tienen de ser normales (Teorema de Crámer).
   • La so diferencia ta de normal distribuyida con ${\displaystyle V=X-Y\sim N(\mu _{X}-\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$ .
   • Si les varianzas de X y Y son iguales, entós O y V son independientes ente sigo.
   • La diverxencia de Kullback-Leibler, ${\displaystyle D{\rm {KL}}(X\|Y)={1 \over 2}\left(\log \left({\sigma _{Y}^{2} \over \sigma _{X}^{2}}\right)+{\frac {\sigma _{X}^{2}}{\sigma _{Y}^{2}}}+{\frac {\left(\mu _{Y}-\mu _{X}\right)^{2}}{\sigma _{Y}^{2}}}-1\right).}$ 
7. Si ${\displaystyle X\sim N(0,\sigma _{X}^{2})}$  y ${\displaystyle Y\sim N(0,\sigma _{Y}^{2})}$  son variables aleatories independientes de normal distribuyíes, entós:
   • El so productu ${\displaystyle XY}$  sigue una distribución con densidá ${\displaystyle p\,}$  dada por
     ${\displaystyle p(z)={\frac {1}{\pi \,\sigma _{X}\,\sigma _{Y}}}\;K_{0}\left({\frac {|z|}{\sigma _{X}\,\sigma _{Y}}}\right),}$  onde ${\displaystyle K_{0}\,}$  ye una función de Bessel modificada de segundu tipu.
   • El so cociente sigue una distribución de Cauchy con ${\displaystyle X/Y\sim \mathrm {Cauchy} (0,\sigma _{X}/\sigma _{Y})\,}$ . D'esta miente la distribución de Cauchy ye un tipu especial de distribución cociente.
8. Si ${\displaystyle X_{1},\dots ,X_{n}}$  son variables normales estándar independientes, entós ${\displaystyle X_{1}^{2}+\cdots +X_{n}^{2}}$  sigue una distribución χ² con n graos de llibertá.
9. Si ${\displaystyle X_{1},\dots ,X_{n}}$  son variables normales estándar independientes, entós la media muestral ${\displaystyle {\bar {X}}=(X_{1}+\cdots +X_{n})/n}$  y la varianza muestral ${\displaystyle S^{2}=((X_{1}-{\bar {X}})^{2}+\cdots +(X_{n}-{\bar {X}})^{2})/(n-1)}$  son independientes. Esta propiedá caracteriza a les distribuciones normales y contribúi a esplicar por qué'l test-F nun ye robezu al respective de la non-normalidá).

Estandarización de variables aleatories normales

De resultes de la Propiedá 1; ye posible rellacionar toles variables aleatories normales cola distribución normal estándar.

Si ${\displaystyle X\,\sim N(\mu ,\sigma ^{2})\,}$ , entós

${\displaystyle Z={\frac {X-\mu }{\sigma }}\!}$ 

ye una variable aleatoria normal estándar: ${\displaystyle Z\,}$  ~ ${\displaystyle N(0,1)\,}$ .

El tresformamientu d'una distribución X ~ N(μ, σ) nuna N(0, 1) llámase normalización, estandarización o tipificación de la variable X.

Una consecuencia importante d'esto ye que la función de distribución d'una distribución normal ye, poro,

${\displaystyle \Pr(X\leq x)=\Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left(1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right).}$ 

A la inversa, si ${\displaystyle Z}$  ye una distribución normal estándar, ${\displaystyle Z}$  ~ ${\displaystyle N(0,1)}$ , entós

${\displaystyle X=\sigma Z+\mu \,}$ 

ye una variable aleatoria normal tipificada de media ${\displaystyle \mu \,}$  y varianza ${\displaystyle \sigma ^{2}\,}$ .

La distribución normal estándar ta tabulada (davezu na forma del valor de la función de distribución Φ) y les otres distribuciones normales pueden llograse como tresformamientos simples, como se describe más arriba, de la distribución estándar. D'esta miente pueden usase los valores tabulados de la función de distribución normal estándar p'atopar valores de la función de distribución de cualesquier otra distribución normal.

Momentos

Los primeres momentos de la distribución normal son:

Númberu	Momentu	Momentu central	Cumulante
0	1	1
1	${\displaystyle \mu }$	0	${\displaystyle \mu }$
2	${\displaystyle \mu ^{2}+\sigma ^{2}}$	${\displaystyle \sigma ^{2}}$	${\displaystyle \sigma ^{2}}$
3	${\displaystyle \mu ^{3}+3\mu \sigma ^{2}}$	0	0
4	${\displaystyle \mu ^{4}+6\mu ^{2}\sigma ^{2}+3\sigma ^{4}}$	${\displaystyle 3\sigma ^{4}}$	0
5	${\displaystyle \mu ^{5}+10\mu ^{3}\sigma ^{2}+15\mu \sigma ^{4}}$	0	0
6	${\displaystyle \mu ^{6}+15\mu ^{4}\sigma ^{2}+45\mu ^{2}\sigma ^{4}+15\sigma ^{6}}$	${\displaystyle 15\sigma ^{6}}$	0
7	${\displaystyle \mu ^{7}+21\mu ^{5}\sigma ^{2}+105\mu ^{3}\sigma ^{4}+105\mu \sigma ^{6}}$	0	0
8	${\displaystyle \mu ^{8}+28\mu ^{6}\sigma ^{2}+210\mu ^{4}\sigma ^{4}+420\mu ^{2}\sigma ^{6}+105\sigma ^{8}}$	${\displaystyle 105\sigma ^{8}}$	0

Tolos cumulantes de la distribución normal, más allá del segundu, son cero.

Los momentos centrales d'orde cimeru (2k con μ = 0) vienen daos pola fórmula

${\displaystyle Y\left[X^{2k}\right]={\frac {(2k)!}{2^{k}k!}}\sigma ^{2k}.}$ 

El Teorema de la Llende Central

 

El Teorema de la llende central establez que so ciertes condiciones (como pueden ser independientes y hermano distribuyíes con varianza finita), la suma d'un gran númberu de variables aleatories distribúyese aproximao como una normal.

La importancia práutica del Teorema de la llende central ye que la función de distribución de la normal puede usase como aproximamientu de delles otres funciones de distribución. Por casu:

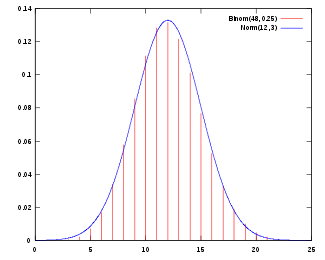
• Una distribución binomial de parámetros n y p ye aproximao normal pa grandes valores de n, y p non demasiáu cercanu a 0 o a 1 (dellos llibros encamienten usar esti aproximamientu namái si np y n(1 − p) son dambos, siquier, 5; nesti casu tendría d'aplicase una correición de continuidá).
  La normal averada tien parámetros μ = np, σ² = np(1 − p).

• Una distribución de Poisson con parámetru λ ye aproximao normal pa grandes valores de λ.
  La distribución normal averada tien parámetros μ = σ² = λ.

La exactitú d'estos aproximamientos depende del propósitu pal que se precisen y de la tasa de converxencia a la distribución normal. Dase'l casu típicu de que tales aproximamientos son menos precises nes coles de la distribución. El Teorema de Berry-Esséen apurre una llende cimera xeneral del error d'aproximamientu de la función de distribución.

Divisibilidad infinita

Les normales tienen una distribución de probabilidá infinitamente divisible: Pa una distribución normal X de media μ y varianza σ² ≥ 0, ye posible atopar n variables aleatories independientes {X₁,...,X_n} caúna con distribución normal de media μ/n y varianza σ²/n yá que la suma X₁ + . . . + X_n d'estes n variables aleatories

${\displaystyle X_{1}+X_{2}+\dots +X_{n}\sim N(\mu ,\sigma ^{2})\,}$ 

tenga esta específica distribución normal (pa verificalo, úsese la función carauterística de convolución y la inducción matemática).

Estabilidá

Les distribuciones normales son puramente estables.

Alredor del 68% de los valores d'una distribución normal tán a una distancia σ < 1 (esviación típica) de la media, μ; alredor del 95% de los valores tán a dos desviación típiques de la media y alredor del 99,7% tán a tres desviación típiques de la media. Esto conozse como la "regla 68-95-99,7" o la "regla empírica".

Pa ser más precisos, l'área so la curva campana ente μ − nσ y μ + nσ en términos de la función de distribución normal vien dada por

${\displaystyle {\begin{aligned}&\Phi _{\mu ,\sigma ^{2}}(\mu +n\sigma )-\Phi _{\mu ,\sigma ^{2}}(\mu -n\sigma )\\&=\Phi (n)-\Phi (-n)=2\Phi (n)-1=\mathrm {erf} {\bigl (}n/{\sqrt {2}}\,{\bigr )},\end{aligned}}}$ 

onde erf ye la función error. Los valores pa n=1, n=2, ... , n= 6, son... (con 12 decimales)...:

${\displaystyle n\,}$	${\displaystyle \mathrm {erf} {\bigl (}n/{\sqrt {2}}\,{\bigr )}\,}$
1	0,682689492137
2	0,954499736104
3	0,997300203937
4	0,999936657516
5	0,999999426697
6	0,999999998027

La siguiente tabla apurre la rellación inversa de múltiples σ correspondientes a unos pocos valores usaos con frecuencia pa l'área so la campana de Gauss. Estos valores son útiles pa determinar intervalo d'enfotu pa los niveles especificaos basaos nuna curva de normal distribuyida (o estimadores asintóticamente normales):

${\displaystyle \mathrm {erf} {\bigl (}n/{\sqrt {2}}\,{\bigr )}}$	${\displaystyle n\,}$
0,80	1,28155
0,90	1,64485
0,95	1,95996
0,98	2,32635
0,99	2,57583
0,995	2,80703
0,998	3,09023
0,999	3,29052
0,9999	3,8906
0,99999	4,4172

onde'l valor a la izquierda de la tabla ye la proporción de valores que van cayer nel intervalu dau y n ye un múltiplu de la esviación típica que determina l'anchor del intervalu.

Forma familia esponencial

La distribución normal tien forma de familia esponencial biparamétrica con dos parámetros naturales, μ y 1/σ², y estadísticos naturales X y X². La forma canónica tien como parámetros ${\displaystyle {\mu \over \sigma ^{2}}}$  y ${\displaystyle {1 \over \sigma ^{2}}}$  y estadísticos suficientes ${\displaystyle \sum x}$  y ${\displaystyle -{1 \over 2}\sum x^{2}.}$ 

Considérese la variable aleatoria complexa gaussiana

${\displaystyle Z=X+iY\,}$ .

onde X y Y son variables gaussianas reales ya independientes con igual varianza ${\displaystyle \sigma _{r}^{2}}$ . La función de distribución de la variable conxunta ye entós

${\displaystyle {\frac {1}{2\,\pi \,\sigma _{r}^{2}}}y^{-(x^{2}+y^{2})/(2\sigma _{r}^{2})}.}$ 

Como ${\displaystyle \sigma _{Z}={\sqrt {2}}\sigma _{r}}$ , la función de distribución resultante pa la variable gaussiana complexa Z ye

${\displaystyle {\frac {1}{\pi \,\sigma _{Z}^{2}}}y^{-|Z|^{2}\!/\sigma _{Z}^{2}}.}$ 

• ${\displaystyle R\sim \mathrm {Rayleigh} (\sigma )\,}$  ye una distribución de Rayleigh si ${\displaystyle R={\sqrt {X^{2}+Y^{2}}}}$  onde ${\displaystyle X\sim N(0,\sigma ^{2})\,}$  y ${\displaystyle Y\sim N(0,\sigma ^{2})\,}$  son dos distribuciones normales independientes.

• ${\displaystyle Y\sim \chi _{\nu }^{2}}$  ye una distribución χ² con ${\displaystyle \nu \,}$  grado de llibertá si ${\displaystyle Y=\sum _{k=1}^{\nu }X_{k}^{2}}$  onde ${\displaystyle X_{k}\sim N(0,1)\,}$  pa ${\displaystyle k=1,\dots ,\nu }$  y son independientes.

• ${\displaystyle Y\sim \mathrm {Cauchy} (\mu =0,\theta =1)\,}$  ye una distribución de Cauchy si ${\displaystyle Y=X_{1}/X_{2}\,}$  pa ${\displaystyle X_{1}\sim N(0,1)\,}$  y ${\displaystyle X_{2}\sim N(0,1)\,}$  son dos distribuciones normales independientes.

• ${\displaystyle Y\sim {\mbox{Log-N}}(\mu ,\sigma ^{2})\,}$  ye una distribución log-normal si ${\displaystyle Y=y^{X}\,}$  y ${\displaystyle X\sim N(\mu ,\sigma ^{2})\,}$ .

• Rellación con una distribución estable: si ${\displaystyle X\sim {\textrm {stable}}(2,\beta ,\sigma /{\sqrt {2}},\mu )}$  entós ${\displaystyle X\sim N(\mu ,\sigma ^{2})\,}$ .

• Distribución normal truncada. si ${\displaystyle X\sim N(\mu ,\sigma ^{2}),\!}$  entós atayando X per debaxo de ${\displaystyle A}$  y percima de ${\displaystyle B}$  va dar llugar a una variable aleatoria de media ${\displaystyle Y(X)=\mu +{\frac {\sigma (\varphi _{1}-\varphi _{2})}{T}},\!}$  onde ${\displaystyle T=\Phi \left({\frac {B-\mu }{\sigma }}\right)-\Phi \left({\frac {A-\mu }{\sigma }}\right),\;\varphi _{1}=\varphi \left({\frac {A-\mu }{\sigma }}\right),\;\varphi _{2}=\varphi \left({\frac {B-\mu }{\sigma }}\right)}$  y ${\displaystyle \varphi \,}$  ye la función de densidá d'una variable normal estándar.

• Si ${\displaystyle X\,}$  ye una variable aleatoria de normal distribuyida y ${\displaystyle Y=|X|\,}$ , entós ${\displaystyle Y\,}$  tien una distribución normal doblada.

Resultaos

De la distribución normal derívense munches resultaos, incluyendo rangos de percentiles ("percentiles" o "cuantiles"), curves normales equivalentes, stanines, z-scores, y T-scores. Amás, un númberu de procedimientos d'estadísticos de comportamientu tán basaos na asunción de qu'eses resultaos tán de normal distribuyíos. Por casu, el test de Student y el analís de varianza (ANOVA) (vease más embaxo). La gradación de la curva campana asigna graos relativos basaos nuna distribución normal de resultaos.

Tests de normalidá

Los tests de normalidá aplicar a conxuntos de datos pa determinar la so semeyanza con una distribución normal. La hipótesis nula ye, nestos casos, si'l conxuntu de datos ye similar a una distribución normal, polo qu'un P-valor abondo pequeñu indica datos non normales.

• Prueba de Kolmogórov-Smirnov
• Test de Lilliefors
• Test de Anderson–Darling
• Test de Ryan–Joiner
• Test de Shapiro–Wilk
• Normal probability plot (rankit plot)
• Test de Jarque–Bera
• Test omnibús de Spiegelhalter

Estimación de parámetro

Estimación de parámetros de máxima verosimilitud

Supóngase que

${\displaystyle X_{1},\dots ,X_{n}}$ 

son independientes y caúna ta de normal distribuyida con media μ y varianza σ ² > 0. En términos estadísticos los valores reparaos d'estes n variables aleatories constitúin una "muestra de tamañu n d'una población de normal distribuyida. Deseyar envalorar la media poblacional μ y la esviación típica poblacional σ, basándose nos valores reparaos d'esta muestra. La función de densidá conxunta d'estes n variables aleatories independientes ye

${\displaystyle {\begin{aligned}f(x_{1},\dots ,x_{n};\mu ,\sigma )&=\prod _{i=1}^{n}\varphi _{\mu ,\sigma ^{2}}(x_{i})\\&={\frac {1}{(\sigma {\sqrt {2\pi }})^{n}}}\prod _{i=1}^{n}\exp {\biggl (}-{1 \over 2}{\Bigl (}{x_{i}-\mu \over \sigma }{\Bigr )}^{2}{\biggr )},\quad (x_{1},\ldots ,x_{n})\in \mathbb {R} ^{n}.\end{aligned}}}$ 

Como función de μ y σ, la función de verosimilitud basada nes observaciones X₁, ..., X_n ye

${\displaystyle L(\mu ,\sigma )={\frac {C}{\sigma ^{n}}}\exp \left(-{\sum _{i=1}^{n}(X_{i}-\mu )^{2} \over 2\sigma ^{2}}\right),\quad \mu \in \mathbb {R} ,\ \sigma >0,}$ 

con dalguna constante C > 0 (de la cual, polo xeneral, dexaríase inclusive que dependiera de X₁, ..., X_n, anque sumiera coles derivaes parciales de la función de log-verosimilitud al respective de los parámetros teníos en cuenta, vease más embaxo).

Nel métodu de máxima verosimilitud, los valores de μ y σ que maximizan la función de verosimilitud tómense como estimadores de los parámetros poblacionales μ y σ.

Davezu na maximización d'una función de dos variables, podríen considerase derivaes parciales. Pero equí esplótase'l fechu de que'l valor de μ que maximiza la función de verosimilitud con σ fixu nun depende de σ. Sicasí, atopamos qu'esi valor de μ, entós sustitúyese por μ na función de verosimilitud y finalmente atopamos el valor de σ que maximiza la espresión resultante.

Rescampla que la función de verosimilitud ye una función decreciente de la suma

${\displaystyle \sum _{i=1}^{n}(X_{i}-\mu )^{2}.\,\!}$ 

Asina que se deseya'l valor de μ que embrive esta suma. Sía

${\displaystyle {\overline {X}}_{n}=(X_{1}+\cdots +X_{n})/n}$ 

la media muestral basada nes n observaciones. Nótese que

${\displaystyle {\begin{aligned}\sum _{i=1}^{n}(X_{i}-\mu )^{2}&=\sum _{i=1}^{n}{\bigl (}(X_{i}-{\overline {X}}_{n})+({\overline {X}}_{n}-\mu ){\bigr )}^{2}\\&=\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2}+2({\overline {X}}_{n}-\mu )\underbrace {\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})} _{=\,0}+\sum _{i=1}^{n}({\overline {X}}_{n}-\mu )^{2}\\&=\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2}+n({\overline {X}}_{n}-\mu )^{2}.\end{aligned}}}$ 

Namái l'últimu términu depende de μ y embrívese por

${\displaystyle {\widehat {\mu }}_{n}={\overline {X}}_{n}.}$ 

Esta ye la estimación de máxima verosimilitud de μ basada nes n observaciones X₁, ..., X_n. Cuando sustituyimos esta estimación por μ na función de verosimilitud, llogramos

${\displaystyle L({\overline {X}}_{n},\sigma )={\frac {C}{\sigma ^{n}}}\exp {\biggl (}-{\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2} \over 2\sigma ^{2}}{\biggr )},\quad \sigma >0.}$ .

Convenir en denotar la "log-función de verosimilitud", esto ye, el llogaritmu de la función de verosimilitud, con una minúscula ℓ, y tenemos

${\displaystyle \ell ({\overline {X}}_{n},\sigma )=\log C-n\log \sigma -{\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2} \over 2\sigma ^{2}},\quad \sigma >0,}$ .

entós

${\displaystyle {\begin{aligned}{\partial \over \partial \sigma }\ell ({\overline {X}}_{n},\sigma )&=-{n \over \sigma }+{\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2} \over \sigma ^{3}}\\&=-{n \over \sigma ^{3}}{\biggl (}\sigma ^{2}-{1 \over n}\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2}{\biggr )},\quad \sigma >0.\end{aligned}}}$ 

Esta derivada ye positiva, cero o negativa según σ² tea ente 0 y

${\displaystyle {\hat {\sigma }}_{n}^{2}:={1 \over n}\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2},}$ 

esto ye igual a esa cantidá, o mayor qu'esa cantidá. (Si hai solamente una observación, lo que significa que n = 1, o si X₁ = ... = X_n, lo cual namái asocede con probabilidad cero, entós ${\displaystyle {\hat {\sigma }}{}_{n}^{2}=0}$  por esta fórmula, reflexa'l fechu de que nestos casos la función de verosimilitud ye ilimitada cuando σ escai hasta cero.)

Consecuentemente esta media de cuadraos de residuos ye'l estimador de máxima verosimilitud de σ², y el so raigañu cuadráu ye'l estimador de máxima verosimilitud de σ basáu nes n observaciones. Esti estimador ${\displaystyle {\hat {\sigma }}{}_{n}^{2}}$  ye sesgado, pero tien un menor error mediu al cuadráu que l'habitual estimador insesgado, que ye n/(n − 1) vegaes esti estimador.

Sorprendente xeneralización

La derivada del estimador de máxima verosimilitud de la matriz de covarianza d'una distribución normal multivariante ye despreciable. Arreya'l teorema espectral y la razón pola que puede ser meyor pa ver un esguilar como la traza d'una matriz 1×1 que como un pixín esguilar. Vease estimación de la covarianza de matrices.

Estimación insesgada de parámetros

El estimador ${\displaystyle {\overline {X}}}$  de máxima verosimilitud de la media poblacional μ, ye un estimador insesgado de la media poblacional.

El estimador de máxima verosimilitud de la varianza ye insesgado si asumimos que la media de la población ye conocida a priori, pero na práutica esto nun asocede. Cuando disponemos d'una muestra y nun sabemos nada de la media o la varianza de la población de la que s'estrayxo, como s'asumía na derivada de máxima verosimilitud de riba, entós el estimador de máxima verosimilitud de la varianza ye sesgado. Un estimador insesgado de la varianza σ² ye la cuasi varianza muestral:

${\displaystyle S^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\overline {X}})^{2}.}$ 

que sigue una distribución Gamma cuando les X_i son normales independientes y hermano distribuyíes:

${\displaystyle S^{2}\sim \operatorname {Gamma} \left({\frac {n-1}{2}},{\frac {2\sigma ^{2}}{n-1}}\right),}$ .

con media ${\displaystyle \operatorname {Y} (S^{2})=\sigma ^{2}}$  y varianza ${\displaystyle \operatorname {Var} (S^{2})=2\sigma ^{4}/(n-1).}$ 

La estimación de máxima verosimilitud de la esviación típica ye'l raigañu cuadráu de la estimación de máxima verosimilitud de la varianza. Sicasí, nin ésta, nin el raigañu cuadráu de la cuasivarianza muestral apurren un estimador insesgado pa la esviación típica (vease estimación insesgada de la esviación típica pa una fórmula particular pa la distribución normal.

Les distribuciones aproximao normales apaecen peruquier, como queda esplicáu pol teorema central de la llende. Cuando nun fenómenu abarrúntase la presencia d'un gran númberu de pequeñes causes actuando de forma aditiva ya independiente ye razonable pensar que les observaciones van ser "normales". Hai métodos estadísticos pa probar empíricamente esta asunción, por casu, el test de D'Agostino-Pearson. El test de Kolmogorov-Smirnov, antes llargamente usáu, agora paez tar desaconseyáu.

Hai causes que pueden actuar de forma multiplicativa (más que aditiva). Nesti casu, l'asunción de normalidá nun ta xustificada y ye el llogaritmu de la variable en cuestión el que taría de normal distribuyíu. La distribución de les variables direutamente reparaes nesti casu denominar log-normal.

Finalmente, si hai una simple influencia esterna que tien un gran efeutu na variable en considerancia, l'asunción de normalidá nun ta tampoco xustificada. Esto ye ciertu inclusive si, cuando la variable esterna caltiénse constante, les distribuciones marxinales resultantes son, n'efeutu, normales. La distribución completa va ser una superposición de variables normales, que nun ye polo xeneral normal. Ello ta rellacionáu cola teoría d'errores (vease más embaxo).

De siguío amuésense una llista de situaciones que taríen, aproximao, de normal distribuyíes. Más embaxo puede atopase un discutiniu detalláu de caúna d'elles:

• En problemes de recuentu, onde'l teorema central de la llende inclúi un aproximamientu de discreta a continua y onde les distribuciones infinitamente divisibles y descomponibles tán arreyaes, tales como:
  • variables aleatories binomiales, acomuñaes con entrugues sí/non;
  • variables aleatories de Poisson, acomuñaes con eventos raros;
• En midíes fisiolóxiques de especímenes biolóxicos:
  • El llogaritmu de les midíes del tamañu de texíos vivos (llargor, altor, superficie de piel, pesu);
  • La llargor d'apéndices inertes (pelo, garres, rabos, dientes) de especímenes biolóxicos na direición del crecimento;
  • Otres midíes fisiolóxiques podríen tar de normal distribuyíes, anque nun hai razón pa esperalo a priori;
• Asumir con frecuencia que los errores de midida tán de normal distribuyíos y cualquier esviación de la normalidá considérase una cuestión que tendría d'esplicase;
• Variables financieres, nel modelu Black-Scholes:
  • Cambeos nel llogaritmu de Cambeos

nel llogaritmu de tases de cambéu, índices de precios, índices d'esistencies de mercáu; estes variables pórtense como l'interés compuestu, non como l'interés simple, por tanto, son multiplicatives;

• • Ente que el modelu Black-Scholes presupon normalidá, en realidá estes variables exhiben coles pesaes, como puede trate en crash de les esistencies de mercáu;
  • Otres variables financieres podríen tar de normal distribuyíes, pero nun hai razón pa esperalo a priori;
• Intensidá de la lluz:
  • La intensidá de la lluz láser ta de normal distribuyida;
  • La lluz térmico tien una distribución de Bose-Einstein n'escales de tiempu bien curtios y una distribución normal en grandes escales de tiempu debíu al teorema central de la llende.

Ye relevante pa la bioloxía y l'economía el fechu de que los sistemes complexos tienden a amosar la llei de potencies más que normal.

Recuentu de fotones

La intensidá de la lluz d'una sola fonte varia col tiempu, según les fluctuaciones térmiques que pueden reparase si la lluz analizar a una resolución abondo altu. La mecánica cuántica interpreta les midíes de la intensidá de la lluz como un recuentu de fotones, onde'l camientu natural lleva a usar la distribución de Poisson. Cuando la intensidá de la lluz integrar a lo llargo de grandes periodos de tiempu mayores que'l tiempu de coherencia, l'aproximamientu Poisson - Normal ye apoderada.

La normalidá ye la asunción central de la teoría matemática d'errores. De forma similar nel axuste de modelos estadísticu, un indicador de la bondá del axuste ye que'l error residual (asina ye como se llamen los errores nesta circunstancia) seya independiente y de normal distribuyíu. L'asunción ye que cualquier esviación de la normalidá precisa ser esplicada. Nesi sentíu, en dambos, axuste de modelos y teoría d'errores, la normalidá ye la única observación que nun precisa ser esplicada, sinón que ye esperada. Sicasí, si los datos orixinales nun tán de normal distribuyíos (por casu, si siguen una distribución de Cauchy, entós los residuos tampoco van tar de normal distribuyíos. Esti fechu ye ignoráu davezu na práutica.

Les midíes repitíes de la mesma cantidá espérase que dexen el pasu a resultaos que tán arrexuntaos en redol a un valor particular. Si toles fontes principales d'errores tomáronse en cuenta, se asume que l'error que queda ten de ser la resultancia d'un gran númberu de bien pequeños y aditivos efeutos y, poro, normal. Les esviaciones de la normalidá interprétense como indicaciones d'errores sistemáticos que nun fueron tomaos en cuenta. Puede aldericase si esta asunción ye válida.

Una famosa observación atribuyida a Gabriel Lippmann diz:^{[ensin referencies]}

Tol mundu cree na llei normal de los errores: los matemáticos, porque piensen que ye un fechu esperimental; y el esperimentadores, porque suponen que ye un teorema matemáticu

Otra fonte podría ser Henri Poincaré.

Carauterístiques físiques de especímenes biolóxicos

Los tamaños de los animales adultos siguen aproximao una distribución log-normal. La evidencia y esplicación basada en modelos de crecedera foi publicada per primer vegada nel llibru Problemes de crecedera relativa, de 1932, por Julian Huxley.

Les diferencies de tamañu por cuenta de dimorfismos sexuales o otros polimorfismos d'inseutos, como la división social de les abeyes n'obreres, zánganos y reines, por casu, fai que la distribución de tamaños esviar escontra la lognormalidad.

L'asunción de que'l tamañu llinial de los especímenes biolóxicos ye normal (más que lognormal) llévanos a una distribución non normal del pesu (yá que el pesu o'l volume ye proporcional al cuadráu o'l cubu del llargor y les distribuciones gaussianas namái caltienen los tresformamientos lliniales). A la inversa, asumir que'l pesu sigue una distribución normal implica llargores non normales. Esto ye un problema porque, a priori, nun hai razón pola que cualesquier d'elles (llargor, masa corporal o otres) tendría de tar de normal distribuyida. Les distribuciones lognormales, per otru llau, caltener ente potencies, asina que el "problema" esmorezse si asume la lognormalidad.

Per otra parte, hai delles midíes biolóxiques onde s'asume normalidá, tales como la presión sanguínea n'humanos adultos. Esta asunción namái ye posible en dixebrando a homes y muyeres en distintes poblaciones, caúna de les cuales ta de normal distribuyida.

Variables financieres

 

Yá en 1900 Louis Bachelier propunxo representar los precios de cambéu usando la distribución normal. Esti aproximamientu modificóse dende entós llixeramente. Por causa de la naturaleza multiplicativa del interés compuestu, los indicadores financieros como valores de mercáu y precios de les materies primes exhiben un "comportamientu multiplicativu". Como tales, los sos cambeos periódicos (por casu, cambeos añales) nun son normales, sinón lognormales. Esta ye inda la hipótesis más comúnmente aceptada en economía.

Sicasí, en realidá les variables financieres exhiben coles pesaes y asina, l'asunción de normalidá infravalora la probabilidá d'eventos estremos como quiebres financieres. Suxuriéronse correiciones a esti modelu per parte de matemáticos como Benoît Mandelbrot, quien reparó que los cambeos nel llogaritmu mientres curtios periodos de tiempu (como un día) avérense bien por distribuciones que nun tienen una varianza finita y, poro, el teorema central de la llende nun puede aplicase. Entá más, la suma de munchos de tales cambeos sigue una distribución de log-Levy.

Distribuciones en tests d'intelixencia

Dacuando, la dificultá y númberu d'entrugues nun test d'intelixencia escuéyese de cuenta qu'apurran resultaos de normal distribuyíos. Entá más, les puntuaciones "en crudu" convertir a valores que marquen el cociente intelectual afaciéndoles a la distribución normal. Sía que non trátase d'una resultancia causada deliberadamente pola construcción del test o d'una interpretación de les puntuaciones que suxure normalidá pa la mayoría de la población. Sicasí, la cuestión alrodiu de si la intelixencia en sí ta de normal distribuyida ye más complicada porque se trata d'una variable latente y, poro, nun puede reparase direutamente.

Ecuación d'espardimientu

La función de densidá de la distribución normal ta estrechamente rellacionada cola ecuación d'espardimientu (homoxénea y isótropa) y, por tanto, tamién cola ecuación de calor. Esta ecuación diferencial parcial describe'l tiempu d'evolución d'una función de densidá baxu espardimientu. En particular, la función de densidá de masa

${\displaystyle \varphi _{0,t}(x)={\frac {1}{\sqrt {2\pi t\,}}}\exp \left(-{\frac {x^{2}}{2t}}\right),}$ 

pa la distribución normal con esperanza 0 y varianza t satisfai la ecuación d'espardimientu:

${\displaystyle {\frac {\partial }{\partial t}}\varphi _{0,t}(x)={\frac {1}{2}}{\frac {\partial ^{2}}{\partial x^{2}}}\varphi _{0,t}(x).}$ 

Si la densidá de masa pa un tiempu t = 0 vien dada pola delta de Dirac, lo cual significa, esencialemente que tola masa ta primeramente concentrada nun puntu, entós la función de densidá de masa nel tiempu t va tener la forma de la función de densidá de la normal, con varianza creciendo linealmente con t. Esta conexón nun ye coincidencia: l'espardimientu deber a un movimientu browniano que queda descritu matemáticamente por un procesu de Wiener, y tal procesu nun tiempu t tamién va resultar normal con varianza creciendo linealmente con t'.

Más xeneralmente, si la densidá de masa inicial vien dada por una función φ(x), entós la densidá de masa nun tiempu t va venir dada pola convolución de φ y una función de densidá normal.

 

Hidroloxía

Na hidroloxía presumir que precipitaciones y descagas de ríos de llarga duración (por casu mensuales o añales) siguen una distribución normal d'alcuerdu al teorema de la llende central.

La imaxe azul ilustra un exemplu del axuste de la distribución normal a datos d'agua mensual d'Ochobre y amuesa los intervalo d'enfotu basaos na distribución binomial.

Xeneración de valores pa una variable aleatoria normal

Pa simulaciones por ordenador ye útil, n'ocasiones, xenerar valores que podríen siguir una distribución anormal. Hai dellos métodos y el más básicu d'ellos ye invertir la función de distribución de la normal estándar p'asina poder realizar la grafica. Conócense otros métodos más eficientes, unu de los cualos ye la tresformamientu de Box-Muller. Un algoritmu inclusive más rápidu ye'l algoritmu zigurat. Dambos alderíquense más embaxo. Un aproximamientu simple a estos métodos ye programalos como sigue: a cencielles súmense 12 esviaciones uniformes (0,1) y réstense 6 (la metá de 12). Esto ye bastante preséu en munches aplicaciones. La suma d'esos 12 valores sigue la distribución de Irwin-Hall; son escoyíos 12 pa dar a la suma una varianza d'unu, esautamente. Les esviaciones aleatories resultantes tán llindaes al rangu (−6, 6) y tienen una densidá que ye una doceava seición d'un aproximamientu polinomial d'undécimu orde a la distribución normal .

El métodu de Box-Muller diz que, si tienes dos númberos aleatorios O y V uniformemente distribuyíos en [0, 1], (por casu, la salida d'un xenerador de númberos aleatorios), entós X y Y son dos variables aleatories estándar de normal distribuyíes, onde:

${\displaystyle X={\sqrt {-2\ln O}}\,\cos(2\pi V).}$ 

${\displaystyle Y={\sqrt {-2\ln O}}\,\sin(2\pi V).}$ 

Esta formulación apaez porque la distribución χ² con dos graos de llibertá (vease la propiedá 4, más arriba) ye una variable aleatoria esponencial fácilmente xenerada (la cual correspuende a la cantidá lnO nestes ecuaciones). Asina, un ángulu escoyíu uniformemente alredor d'un círculu vía la variable aleatoria V y un radiu escoyíu pa ser esponencial tresfórmense entós en coordenaes x y y de normal distribuyíes.

Un métodu muncho más rápido que'l tresformamientu de Box-Muller, pero que sigue siendo exactu ye'l llamáu algoritmu Zigurat, desenvueltu por George Marsaglia. N'alredor del 97% de los casos usa namái dos númberos aleatorios, un enteru aleatoriu y un uniforme aleatoriu, una multiplicación y un test-si . Namái un 3% de los casos onde la combinación d'estos dos cai fora del "corazón del zigurat", un tipu de refuga muestral usando llogaritmos, esponenciales y númberos aleatorios más uniformes tendríen de ser emplegaos.

Hai tamién dalguna investigación sobre la conexón ente la rápida tresformamientu de Hadamard y la distribución normal, en virtú de que'l tresformamientu emplega namái adición y sustracción y pol teorema central de la llende los númberos aleatorios de cuasi cualquier distribución van ser tresformaos na distribución normal. Nesta visión pueden combinase una serie de tresformamientos de Hadamard con permutaciones aleatories pa devolver conxuntos de datos aleatorios de normal distribuyíos.

Aproximamientos numbéricos de la distribución normal y la so función de distribución

La función de distribución normal úsase estensamente en computación científica y estadística. Poro, foi implementada de delles formes.

Abramowitz y Stegun (1964) dan la conocida como "meyor aproximamientu de Hastings" para Φ(x) con x > 0 con un error absolutu |ε(x)| < 7.5·10⁻⁸ (algoritmu 26.2.17):

${\displaystyle \Phi (x)=1-\phi (x){\Big (}b_{1}t+b_{2}t^{2}+b_{3}t^{3}+b_{4}t^{4}+b_{5}t^{5}{\Big )}+\varepsilon (x),\qquad t={\frac {1}{1+b_{0}x}},}$ 

onde ϕ(x) ye la función de densidá de la distribución normal estándar, :${\displaystyle \phi (x)={\tfrac {1}{\sqrt {2\pi }}}\,y^{-{\frac {\scriptscriptstyle 1}{\scriptscriptstyle 2}}x^{2}}}$  y les constantes son b₀ = 0.2316419, b₁ = 0.319381530, b₂ = −0.356563782, b₃ = 1.781477937, b₄ = −1.821255978, b₅ = 1.330274429.

La Biblioteca Científica GNU calcula valores de la función de distribución normal estándar usando aproximamientos por funciones racionales a cachos. Otru métodu d'aproximamientu usa polinomios de tercer grau n'intervalos. L'artículu sobre'l llinguaxe de programación bc apurre un exemplu de cómo computar la función de distribución en GNU bc.

Pa un discutiniu más detalláu sobre cómo calcular la distribución normal, vease la seición 3.4.1C. de The Art of Computer Programming (L'arte de la programación por ordenador), de Knuth.

• Carl Friedrich Gauss
• Cociente intelectual
• Desenfoque gaussiano y convolución usando la distribución normal como nucleu.
• Distribución χ²
• Distribución loxística
• Distribución log-normal
• Distribución normal multivariante
• Distribución t de Student
• Función gaussiana (campana de Gauss)
• Función logit
• Función probit
• Gráficu de probabilidá normal
• Iannis Xenakis, distribución gaussiana en música
• Procesu de Gauss
• Prueba de Mann-Whitney Métodu non paramétrico qu'avera a una normal
• Tabla distribución normal tipificada
• Tamañu de la muestra
• Teorema Central de la Llende
• Tables estadístiques

• Graficadora de la distribución normal - CalEst na Web
• Calculadora de distribuciones (discretes y continues) - CalEst na Web
• Graficadora d'una o delles distribuciones normales - CalEst na Web
• Árees so la curva normal Tabla conteniendo los valores de la función normal
• Calculadora de probabilidaes nuna distribución Normal. Dexa faer cálculos direutos ya inversos.
• DynStats: Llaboratoriu estadísticu online con calculadora de funciones de distribución
• Tabla de la distribución normal Tabla de la distribución normal en formatu PDF

Axuste por software d'una distribución de probabilidá a un conxuntu de datos

• Easy fit, "data analysis & simulation"
• MathWorks Benelux (enllaz rotu disponible n'Internet Archive; ver l'historial y la última versión).
• ModelRisk, "risk modelling software"
• Ricci distributions, fitting distrubutions with R , Vito Ricci, 2005
• Risksolver, automatically fit distributions and parameters to samples
• StatSoft distribution fitting
• CumFreq , llibre ensin costu, inclúi la distribución normal, la lognormal, raigañu-normal, cuadráu-normal, y intervalo d'enfotu a base de la distribución binomial
• Calculadora Distribución normal
• Calcular la probabilidá d'una distribución normal con R (llinguaxe de programación)
• Implementación Real en C del algoritmu Expectation Maximization (EM) pa envalorar Gaussian Mixture Models (GMMs).