Find the Slope of a Line
Find the Slope of a Line - Search results - Wiki Find The Slope Of A Line
Did you mean: find the slopes of a life
The page "Find+the+Slope+of+a+Line" does not exist. You can create a draft and submit it for review or request that a redirect be created, but consider checking the search results below to see whether the topic is already covered.
- Partial derivative (category Pages using sidebar with the child parameter)parallel to the yz-plane (which result from holding either y or x constant, respectively). To find the slope of the line tangent to the function at P(1...
Differential calculus (redirect from Increments, Method of)value. The process of finding a derivative is called differentiation. Geometrically, the derivative at a point is the slope of the tangent line to the graph...
In a slippery slope argument, a course of action is rejected because the slippery slope advocate believes it will lead to a chain reaction resulting in...
Park Slope is a neighborhood in western Brooklyn, New York City, within the area once known as South Brooklyn. Park Slope is roughly bounded by Prospect...- Tangent (redirect from Tangent line)at a point x = c if the line passes through the point (c, f(c)) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition...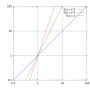
Log–log plot (category Logarithmic scales of measurement)is the slope of the line (gradient) and b = log a is the intercept on the (log y)-axis, meaning where log x = 0, so, reversing the logs, a is the y value...
The Seventh Avenue station (also Seventh Avenue–Park Slope station) is an express station on the IND Culver Line of the New York City Subway, located...- has slope −a/b, so any line perpendicular to it will have slope b/a (the negative reciprocal). Let (m, n) be the point of intersection of the line ax +...
Slope County is a county in the U.S. state of North Dakota. As of the 2020 census, the population was 706, making it the least populous county in North...- measurements for the effect of slope angle, expansion or contraction due to temperature, and the tape's sag, which varies with the applied tension. Not...
- the lasing threshold, the resulting curve is usually close to a straight line. The slope efficiency is the slope of this line. Slope efficiency can similarly...
the slope of the fitted line is equal to the correlation between y and x corrected by the ratio of standard deviations of these variables. The intercept...
located in the southern part of the modern borough. Boerum Hill Carroll Gardens Columbia Street Waterfront District Cobble Hill Gowanus Park Slope South Park...
A slope field (also called a direction field) is a graphical representation of the solutions to a first-order differential equation of a scalar function...- with the Euler estimate of the next point to give the slope of the tangent line at the right end-point. Next the average of both slopes is used to find the...
- A reverse slope defence is a military tactic where a defending force is positioned on the slope of an elevated terrain feature such as a hill, ridge, or...
- Linear regression (redirect from Line of regression)observations. The Theil–Sen estimator is a simple robust estimation technique that chooses the slope of the fit line to be the median of the slopes of the lines...
- Calculus (redirect from The calculus)Geometrically, the derivative is the slope of the tangent line to the graph of f at a. The tangent line is a limit of secant lines just as the derivative is a limit...
- The visual approach slope indicator (VASI) is a system of lights on the side of an airport runway threshold that provides visual descent guidance information...
- to a given curve. He could then use the radius at the point of intersection to find the slope of a normal line, and from this one can easily find the slope...
- The Forth Bridge by Wilhelm Westhofen Site of Bridge and Profile on Centre Line 1684928The Forth Bridge — Site of Bridge and Profile on Centre LineWilhelm
- between the two possible directions in the line of a given slope. Thus... we should say specifically "direction of an unoriented straight line" and not
- Algebra Slope is the measure of how much a line moves up or down related to how much it moves left to right. In this image, the slope of the line is